二元一次方程组和一次函数

(共32张PPT)
1、方程组 有 个解；
2、方程组 有 个解；
3、方程组 有 个解；
0
无数
一
两条直线互相平行，有 交点；
两条直线重合，有 交点；
两条直线相交，有 交点；
0个
无数个
一个
7.6 二元一次方程与一次函数（1）
x+y=5这是什么？
一次函数
这是怎么回事？
二元一次方程
方程x+y=5可以转化为
任意一个二元一次方程都可以转化成y=kx+b的形式,所以每个二元一次方程都对应一个一次函数.
归纳:
思考：是不是任意的二元一次方程都能进行这样的转换呢？
y=5-x
师生互动
师 1)方程X+Y=5的解有 无数多个解 , (0,5) 、(5,0) 、(1,4) 。。。。。。。.
(2)在直角坐标系中分别描出以这些解为坐标的点,它们都在函数Y=5-X上吗
(0,5) 、(5,0) 、(1,4) .都在函数Y=5-X的图象上.
(3)在一次函数Y=5-X的图象上任取一个点,它的坐标适合方程X+Y=5吗
在一次函数Y=5-X的图象上任取一个点(0,5),它的坐标适合方程X+Y=5.
(4)以方程X+Y=5的解为坐标的所有的点所组成的图象与一次函数Y=5-X的图象相同吗
过(0,5) 、(5,0) 两点的直线图象与一次函数Y=5-X的图象相同.
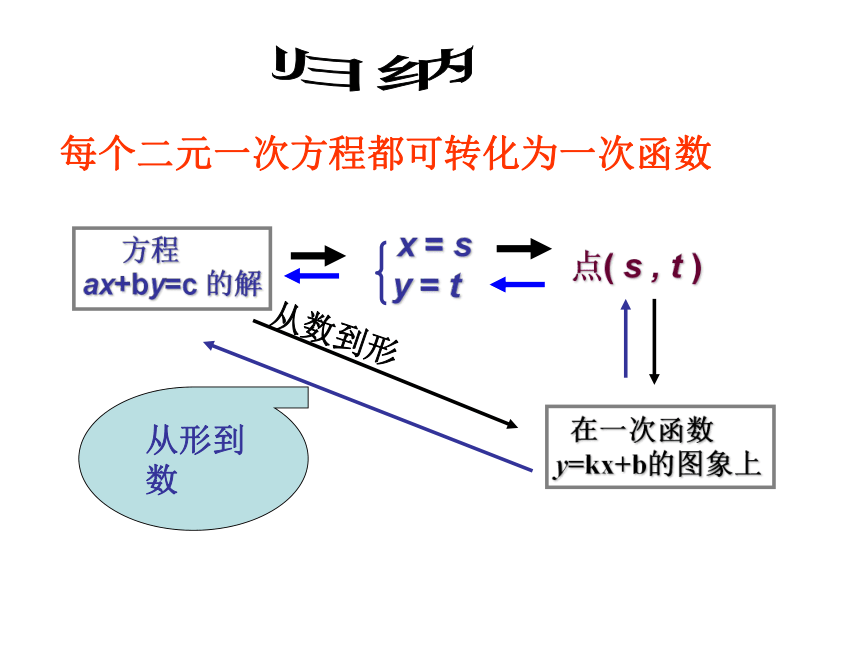
在一次函数
y=kx+b的图象上
点( s , t )
x = s
y = t
方程
ax+by=c 的解
从形到数
从数到形
每个二元一次方程都可转化为一次函数
知识源于悟
益智的“机会”
师:通过以上结论,你能分析研究出二元一次方程与一次函数图象的关系吗
生:二元一次方程的解就是一次函数图象的点的 坐标;一次函数图象上的点的坐标就是二元一次方程的解.
二元一次方程与一次函数的基本关系
x+y=5
y=5-x
2x-y=1
y=2x-1
x=0
y=5
x=5
y=0
x=0
y=-1
x=0.5
y=0
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
y=2x-1
y=5-x
P(2,3)
x+y=5
2x-y=1
x=2
y=3
的解
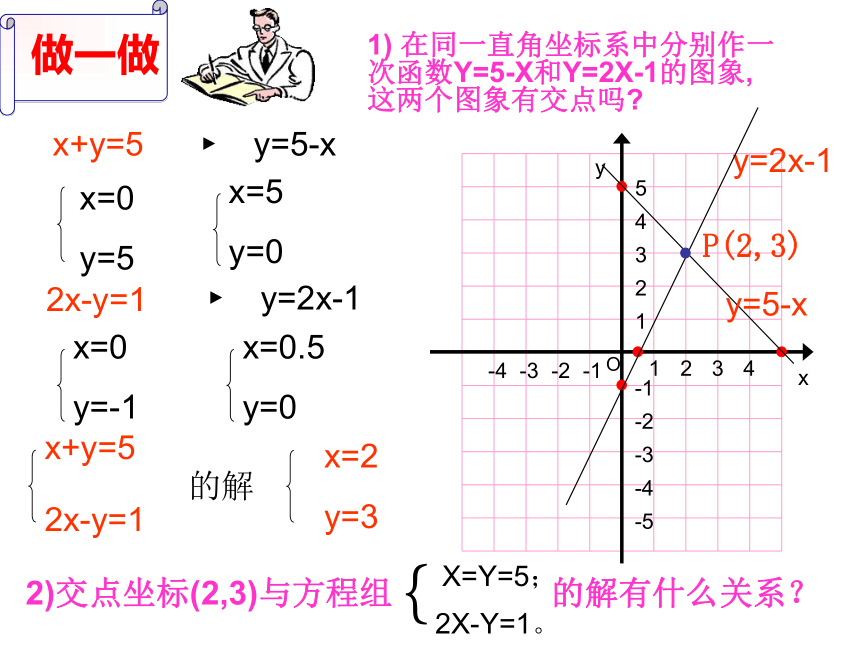
做一做
2)交点坐标(2,3)与方程组 的解有什么关系？
｛
X=Y=5；
2X-Y=1。
1) 在同一直角坐标系中分别作一次函数Y=5-X和Y=2X-1的图象,这两个图象有交点吗
在同一直角坐标系中一次函数Y=5-X和Y=2X-1的图象有交点，交点坐标是（2，3）。
方程组 的解是
｛
X+Y=5；
2X-Y=1。
｛
X=2；
Y=3。
交点坐标(2,3)是方程组 的解
｛
X+Y=5；
2X-Y=1。
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
P(2,2)
y=2x-2
x=2
y=2
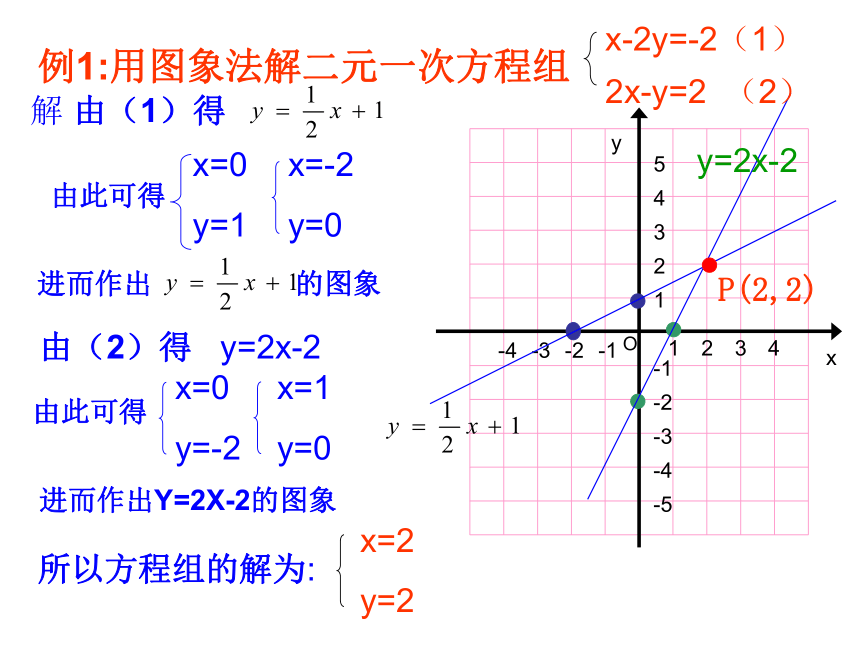
所以方程组的解为:
由（2）得 y=2x-2
x=0
y=-2
x=1
y=0
由此可得
进而作出Y=2X-2的图象
x=0
y=1
x=-2
y=0
由此可得
解 由（1）得
进而作出 的图象
x-2y=-2（1）
2x-y=2 （2）
例1:用图象法解二元一次方程组
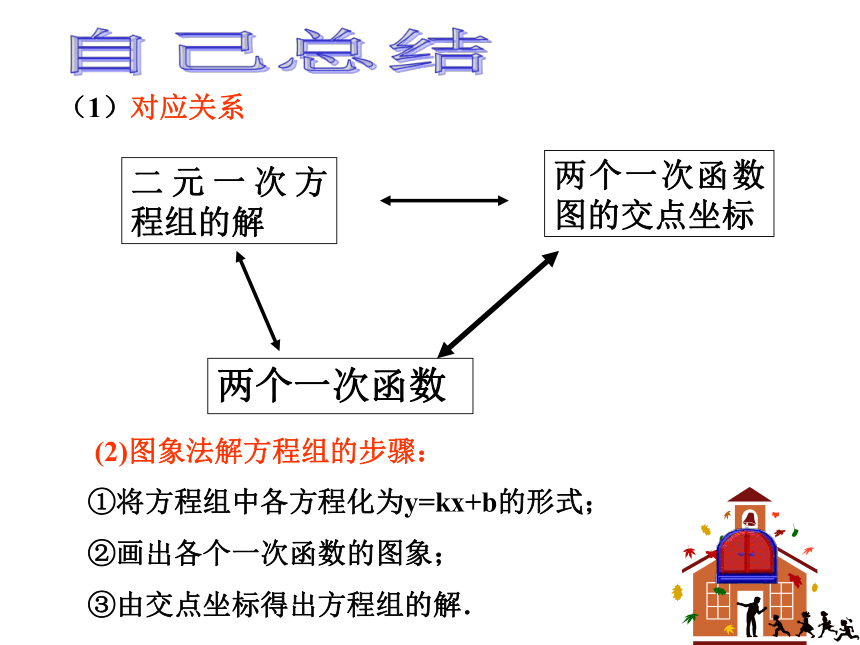
（1）对应关系
①将方程组中各方程化为y=kx+b的形式；
②画出各个一次函数的图象；
③由交点坐标得出方程组的解．
二元一次方程组的解
两个一次函数图的交点坐标
两个一次函数
(2)图象法解方程组的步骤：
1、一次函数y=5-x与y=2x-1图象的交点为(2,3),
则方程组 的解为 .
2、若二元一次方程组 的解为 ,
则函数 与 的图象的交点坐标为 .
（2，2）
3．根据下列图象，你能说出是哪些方程组的解 这些解是什么
1
1
x
y
0
-2
1
x
y
0
求直线 与 直线的交点坐标。你有哪些方法 与同伴交流，并一起分析各种方法的利弊．
解法思路2：由解方程组，得到交点坐标．(把形的问题归结为数的解决，便捷准确)
解法思路l：画出图象找出交点，确定交点坐标近似值．(因作图误差可能有较大差别)
议一议：
A、B 两地相距150千米，甲、乙两人骑自行车分别从A、B 两地相向而行。假设他们都保持匀速行驶，则他们各自到A地的距离 s(千米)都是骑车时间 t (时)的一次函数.
1 时后乙距A地120千米,
2 时后甲距A地 40千米.
问：经过多长时间两人相遇
议一议：
A、B 两地相距150千米，甲、乙两人骑自行车分别从A、B 两地相向而行。假设他们都保持匀速行驶，则他们各自到A地的距离 s(千米)都是骑车时间 t (时)的一次函数.
1 时后乙距A地120千米,
2 时后甲距A地 40千米.
问：经过多长时间两人相遇
直线型图表示
B
乙
甲
A
120千米
2时,40千米
1时
A、B 两地相距150千米，甲、乙两人骑自行车分别从A、B 两地相向而行。假设他们都保持匀速行驶，则他们各自到A地的距离s(千米)都是骑车时间t(时)的一次函数.
1 时后乙距A地120千米,
2 时后甲距A地 40千米.
问 经过多长时间两人相遇
用图象法 解 行程问题
0
4
1
2
3
l1
l2
t
s
140
120
100
80
60
40
20
150
图象表示
(A)
(B)
可以分别作出两人
s 与t 之间的关系图象，
找出交点的横坐标就行了！
你明白他的想法吗？
用他的方法做一做，
看看和你的结果一致吗？
小明的方法求出的结果准确吗？
1
2
3
A、B 两地相距150千米，甲、乙两人骑自行车分别从A、B 两地同时相向而行。假设他们都保持匀速行驶，则他们各自到A地的距离s(千米)都是骑车时间t(时)的一次函数.
1 时后乙距A地120千米,
2 时后甲距A地 40千米.
问 经过多长时间两人相遇
用方程 解 行程问题
小彬
1 时后乙距A地
120千米,即乙的
速度是 30千米/时,
2 时后甲距A 地 40千米,
故甲的速度是 20千米/时,
由此可求出甲、乙两人的速度, 以及
……
你明白他的想法吗？用他的方法做一做，看看和你的结果一致吗？
t=3
A、B 两地相距150千米，甲、乙两人骑自行车分别从A、B 两地相向而行。假设他们都保持匀速行驶，则他们各自到A 地的距离s (千米) 都是骑车时间 t (时) 的一次函数.
1 时后乙距A地120千米,
2 时后甲距A地 40千米.
问 经过多长时间两人相遇
求出s与t之间的关系式，联立解方程组
你明白他的想法吗？
用他的方法做一做，
看看和你的结果一致吗？
对于乙，s 是t
的一次函数，
可设 s=kt+b。
当t=0时，s=150；
当t=1时，s=120。将它们分别代入s=kt+b中，可以求出k、b的值，也即可以求出乙 s 与t 之间的函数表达式。
同样可求出甲s与t之间的函数表达式。
再联立这两个表达式，求解方程组就行了。
小颖
消去 s
用一元一次方程的方法可以解决问题
用图象法可以解决问题
用方程组的方法可以解决问题
小明
小彬
小颖
用作图象的方法可以直观地获得问题的结果，但有时却难以准确，为了获得准确的结果，我们一般用代数方法。
在以上的解题过程中你受到什么启发？
x/ 吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
P173引例.
如图，l11反映了某公司产品的销售收入与销售量的关系，
l11
l22
当销售量为　 　时，销售收入等于销售成本。
　　　　
l22反映了该公司产品的销售成本与销售量的关系，根据图意填空：
你有什么新的方法解决以前的问题吗？
4000
下图中 l1 ，l2 分别表示 B 离岸起两船相对于海岸的距离ｓ与追赶时间ｔ之间的关系。
根据图象回答下列问题：
海
岸
公
海
A
B
2
4
6
8
10
O
2
4
6
8
t /分
s /海里
l11
l22
Ｂ
Ａ
当时间t等于多少分钟时，我边防快艇B能够追赶上A。
P174例2：
你有什么新的方法解决以前的问题吗？
思考题：
1、某区中学生足球赛共赛8轮（即每队均需参赛8场），胜一场得3分，平一场得1分，负一场得0分。在这次足球联赛中，猛虎队踢平的场数是所负场数的2倍，共得17分，试问该队胜了几场？（要求用图象法求解）
思考题：
1、某区中学生足球赛共赛8轮（即每队均需参赛8场），胜一场得3分，平一场得1分，负一场得0分。在这次足球联赛中，猛虎队踢平的场数是所负场数的2倍，共得17分，试问该队胜了几场？（要求用图象法求解）
解：设：胜x场，负y场，则平2y场。
根据题意得：
0
3
5
1
8/3
4
2
2
x
y
17/2
（2004年湖北省国家课改实验区中考题）
思考题：
2、已知方程组 ，所对应的一次函数的图象表示如图，试求出a-b的值。
0
1/2
-1
X
Y
（2004年贵阳市中考试题）
知识的升华
小结 拓展
1) 二元一次方程与一次函数的区别与联系
二元一次方程的解是一次函数上点的坐标; 一次函数上每一个点的坐标就是二元一次方程的一组解.
2) 二元一次方程组的解法总共学习了哪几种
加减法;代入法;图象法.
3) 方法归纳
用图象法解二元一次方程组
优点:方法简便,形象直观;体现了数形结合思想.
不足:一般情况下求出的是近似数;要想精确还要用代 数方法,进行细致计算.
议一议:二元一次方程组的一般形式是
将上述三个方程组的系数与它的解的情况进行比较,猜想出方程
组的系数与解的个数之间的关系.
结论:
(1)当
时方程组有一组解
(3)当
时方程组无解
(2)当
时方程组有无数组解
课外思考题（备用题）
1、用作图象法解方程组
课外思考题（备用题）
2、如图，L1和L2分别表示甲走路和乙骑自行车（在同一条路上）行走的路程s（千米）与时间t（小时）之间的关系，观察图象，回答下列问题：
（1）途中乙发生了什么事，
（2）他们是相遇还是追击；
（3）他们几时相遇。
0
t
s
10
8
12
0.5
1
1.2
A
B
D
E
P
作业
课本:P240习题7.7 （1、2）