北师大版数学九年级下册 1.1 .2 正弦、余弦 复习练习题(Word版 含答案)
文档属性
| 名称 | 北师大版数学九年级下册 1.1 .2 正弦、余弦 复习练习题(Word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 144.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-05 00:00:00 | ||
图片预览


文档简介
第一章 直角三角形的边角关系 1.2 正弦、余弦
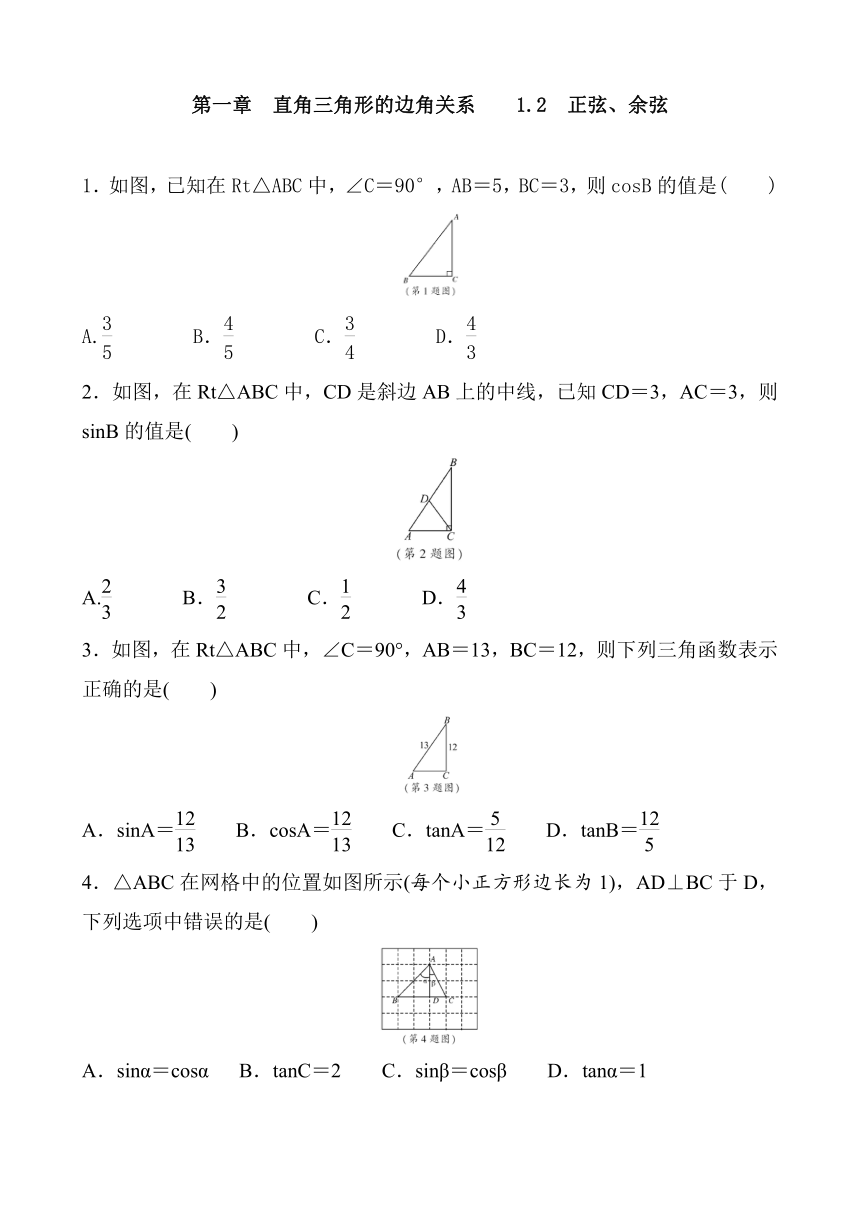
1.如图,已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值是( )
A. B. C. D.
2.如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=3,AC=3,则sinB的值是( )
A. B. C. D.
3.如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是( )
A.sinA= B.cosA= C.tanA= D.tanB=
4.△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列选项中错误的是( )
A.sinα=cosα B.tanC=2 C.sinβ=cosβ D.tanα=1
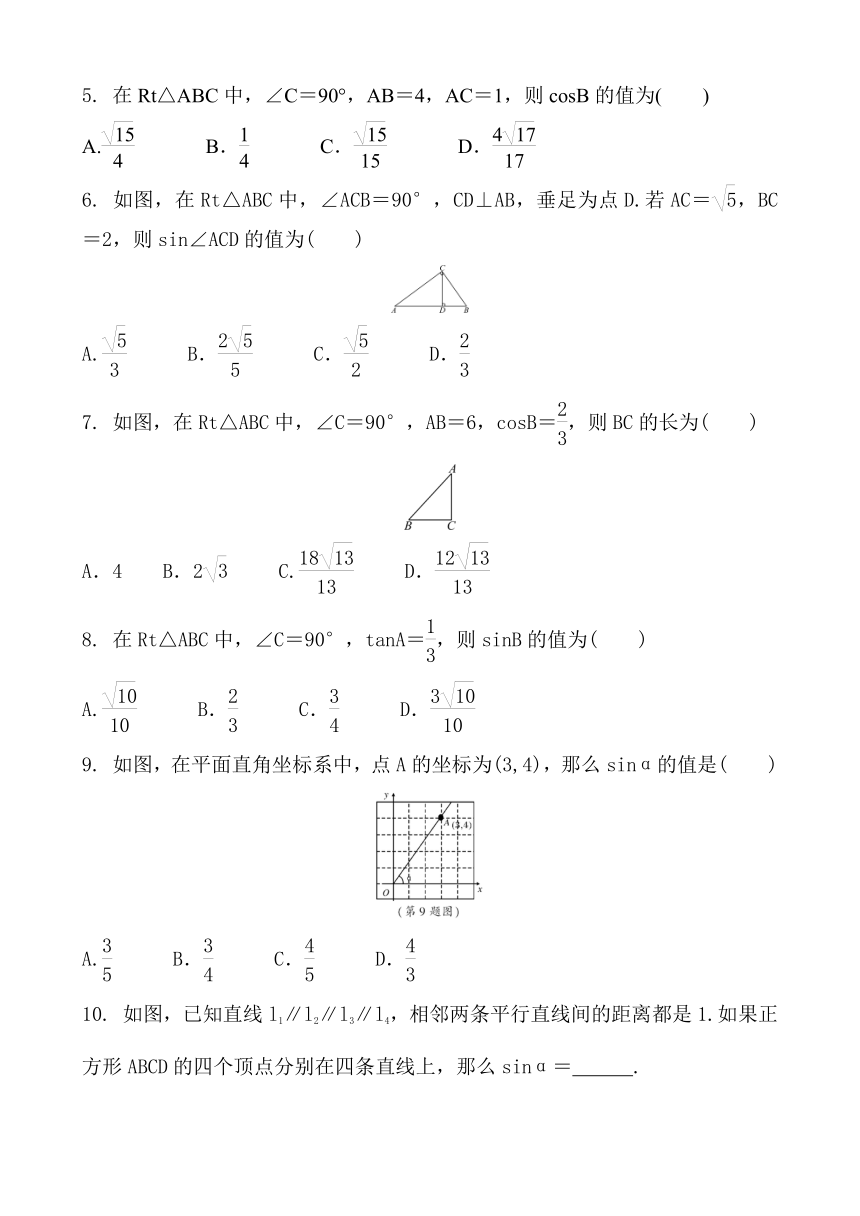
5. 在Rt△ABC中,∠C=90°,AB=4,AC=1,则cosB的值为( )
A. B. C. D.
6. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D.若AC=,BC=2,则sin∠ACD的值为( )
A. B. C. D.
7. 如图,在Rt△ABC中,∠C=90°,AB=6,cosB=,则BC的长为( )
A.4 B.2 C. D.
8. 在Rt△ABC中,∠C=90°,tanA=,则sinB的值为( )
A. B. C. D.
9. 如图,在平面直角坐标系中,点A的坐标为(3,4),那么sinα的值是( )
A. B. C. D.
10. 如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1.如果正方形ABCD的四个顶点分别在四条直线上,那么sinα= .
11. 在△ABC中,∠C=90°,BC=6cm,sinA=,则AB的长是 cm.
12. 在Rt△ABC中,∠C=90°,若AB=10,sinB=,则BC= .
13. 如图,在四边形ABCD中,E、F分别是AB、AD的中点.若EF=2,BC=5,CD=3,则cosC的值为 .
14. 如图,在Rt△ABC中,∠C=90°,a∶c=2∶3.求∠A、∠B的正弦值与余弦值.
15. 如图,在Rt△ABC中,BC、AC、AB三边的长分别为a、b、c,则sinA=,cosA=,tanA=.我们不难发现:sin260°+cos260°=1,…试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
16. 在△ABC中,∠C=90°,cosA=,AC=6.求△ABC的周长和面积.
17. 如图,在直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=.
求:(1)点B的坐标;
(2)cos∠BAO的值.
18. 如图,在Rt△ABC中,∠ACB=90°,D是边AB的中点,BE⊥CD,垂足为点E.已知AC=15,cosA=.
(1)求线段CD的长;
(2)求sin∠DBE的值.
答案:
1---9 ACACA AADC
10.
11. 10.
12. 6
13.
14. 解:∵a∶c=2∶3,∴sinA=,cosB=.设a=2k,c=3k,由勾股定理得b==k,∴cosA=,sinB=.
15. 解:sin2A+cos2A=1,tanA=.理由略.
16. 解:在Rt△ABC中,因为∠C=90°,cosA==,又因为AC=6,
所以AB=10,由勾股定理,得BC==8,
所以△ABC的周长为AB+BC+AC=10+8+6=24,
S△ABC=BC·AC=×8×6=24.
17. 解:(1)作BH⊥OA,垂足为H,在Rt△OHB中,∵OB=5,sin∠BOA=,
∴BH=3,∴OH=4,∴点B的坐标为(4,3);
(2)∵OA=10,OH=4,AH=6,在Rt△AHB中,∵BH=3,∴AB=3,
∴cos∠BAO==.
18. 解:(1)cosA==,∴AB=25,∴CD=BD=AB=;
(2)由CD=BD=AB得∠ABC=∠BCE,易证△ABC∽△BCE,=,∴CE=16,∴DE=16-=,∴sin∠DBE==.
1.如图,已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值是( )
A. B. C. D.
2.如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=3,AC=3,则sinB的值是( )
A. B. C. D.
3.如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是( )
A.sinA= B.cosA= C.tanA= D.tanB=
4.△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列选项中错误的是( )
A.sinα=cosα B.tanC=2 C.sinβ=cosβ D.tanα=1
5. 在Rt△ABC中,∠C=90°,AB=4,AC=1,则cosB的值为( )
A. B. C. D.
6. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D.若AC=,BC=2,则sin∠ACD的值为( )
A. B. C. D.
7. 如图,在Rt△ABC中,∠C=90°,AB=6,cosB=,则BC的长为( )
A.4 B.2 C. D.
8. 在Rt△ABC中,∠C=90°,tanA=,则sinB的值为( )
A. B. C. D.
9. 如图,在平面直角坐标系中,点A的坐标为(3,4),那么sinα的值是( )
A. B. C. D.
10. 如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1.如果正方形ABCD的四个顶点分别在四条直线上,那么sinα= .
11. 在△ABC中,∠C=90°,BC=6cm,sinA=,则AB的长是 cm.
12. 在Rt△ABC中,∠C=90°,若AB=10,sinB=,则BC= .
13. 如图,在四边形ABCD中,E、F分别是AB、AD的中点.若EF=2,BC=5,CD=3,则cosC的值为 .
14. 如图,在Rt△ABC中,∠C=90°,a∶c=2∶3.求∠A、∠B的正弦值与余弦值.
15. 如图,在Rt△ABC中,BC、AC、AB三边的长分别为a、b、c,则sinA=,cosA=,tanA=.我们不难发现:sin260°+cos260°=1,…试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
16. 在△ABC中,∠C=90°,cosA=,AC=6.求△ABC的周长和面积.
17. 如图,在直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=.
求:(1)点B的坐标;
(2)cos∠BAO的值.
18. 如图,在Rt△ABC中,∠ACB=90°,D是边AB的中点,BE⊥CD,垂足为点E.已知AC=15,cosA=.
(1)求线段CD的长;
(2)求sin∠DBE的值.
答案:
1---9 ACACA AADC
10.
11. 10.
12. 6
13.
14. 解:∵a∶c=2∶3,∴sinA=,cosB=.设a=2k,c=3k,由勾股定理得b==k,∴cosA=,sinB=.
15. 解:sin2A+cos2A=1,tanA=.理由略.
16. 解:在Rt△ABC中,因为∠C=90°,cosA==,又因为AC=6,
所以AB=10,由勾股定理,得BC==8,
所以△ABC的周长为AB+BC+AC=10+8+6=24,
S△ABC=BC·AC=×8×6=24.
17. 解:(1)作BH⊥OA,垂足为H,在Rt△OHB中,∵OB=5,sin∠BOA=,
∴BH=3,∴OH=4,∴点B的坐标为(4,3);
(2)∵OA=10,OH=4,AH=6,在Rt△AHB中,∵BH=3,∴AB=3,
∴cos∠BAO==.
18. 解:(1)cosA==,∴AB=25,∴CD=BD=AB=;
(2)由CD=BD=AB得∠ABC=∠BCE,易证△ABC∽△BCE,=,∴CE=16,∴DE=16-=,∴sin∠DBE==.
