人教版七年级下册数学课件:5.3.1:平行线的性质(16张)
文档属性
| 名称 | 人教版七年级下册数学课件:5.3.1:平行线的性质(16张) | 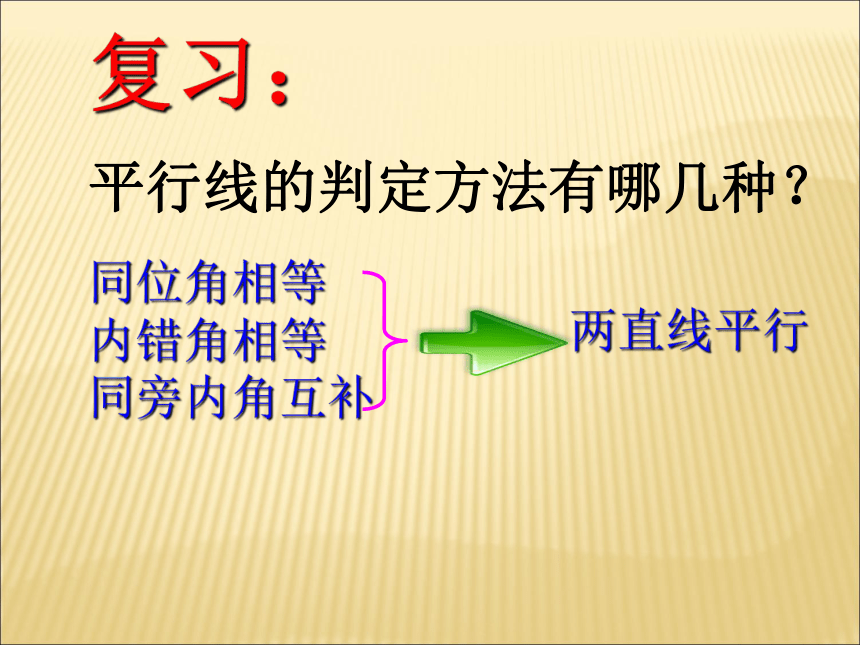 | |
| 格式 | ppt | ||
| 文件大小 | 812.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-05 21:25:28 | ||
图片预览


文档简介
同位角相等
内错角相等
同旁内角互补
两直线平行
平行线的判定方法有哪几种?
复习:
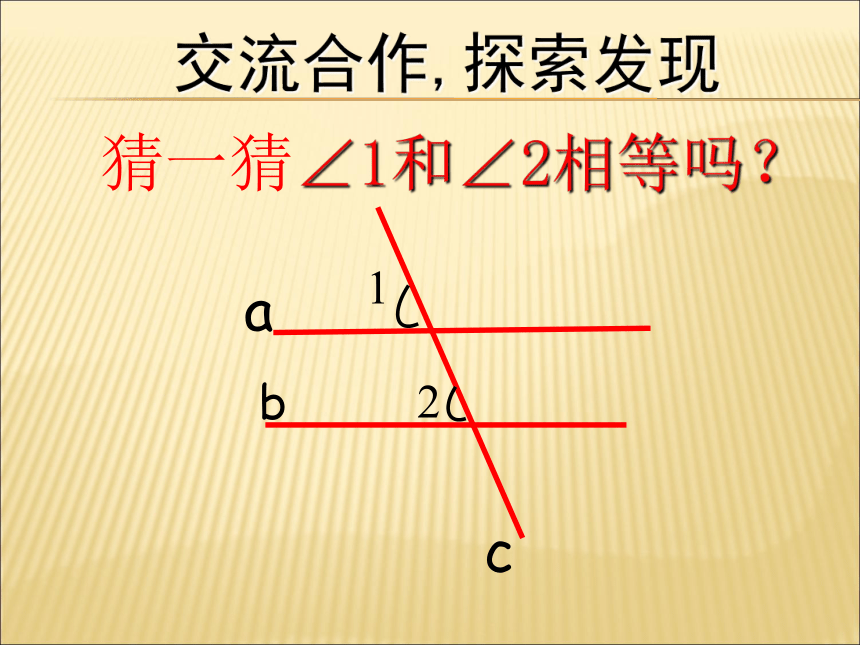
猜一猜∠1和∠2相等吗?
b
1
2
a
c
交流合作,探索发现
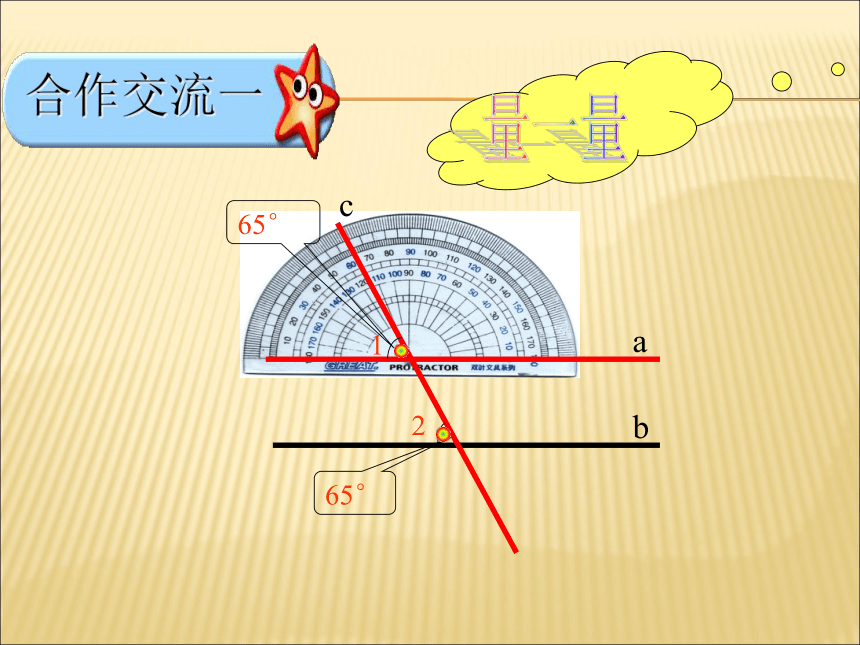
65°
65°
c
a
b
1
2
合作交流一
量一量
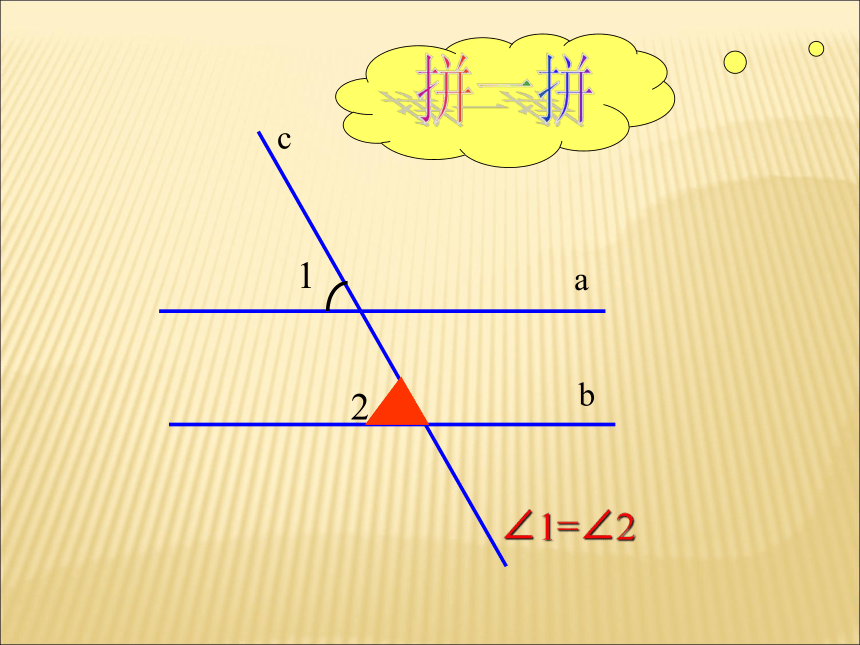
b
2
a
c
1
拼一拼
∠1=∠2
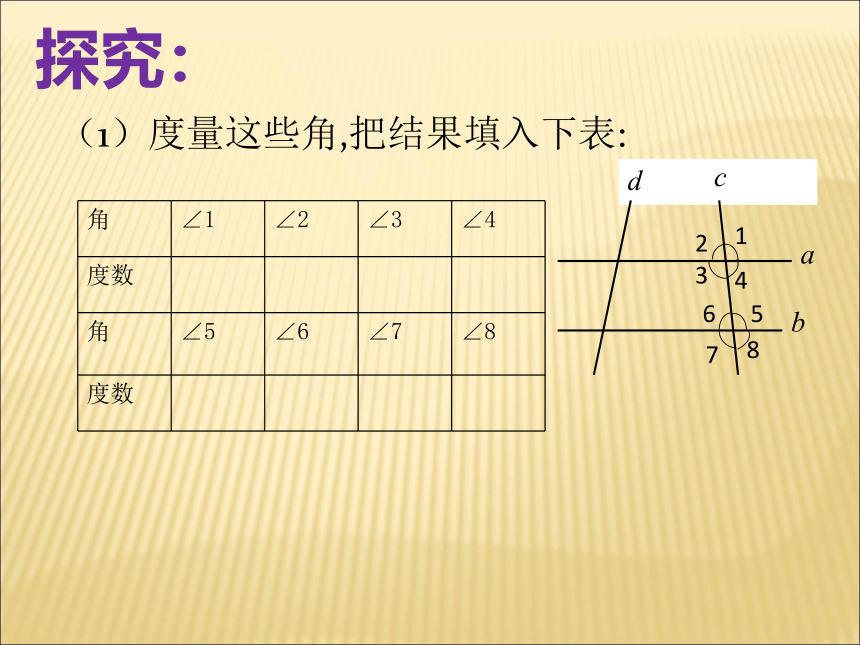
(1)度量这些角,把结果填入下表:
角
∠1
∠2
∠3
∠4
度数
角
∠5
∠6
∠7
∠8
度数
a
8
3
2
1
7
d
6
5
4
b
c
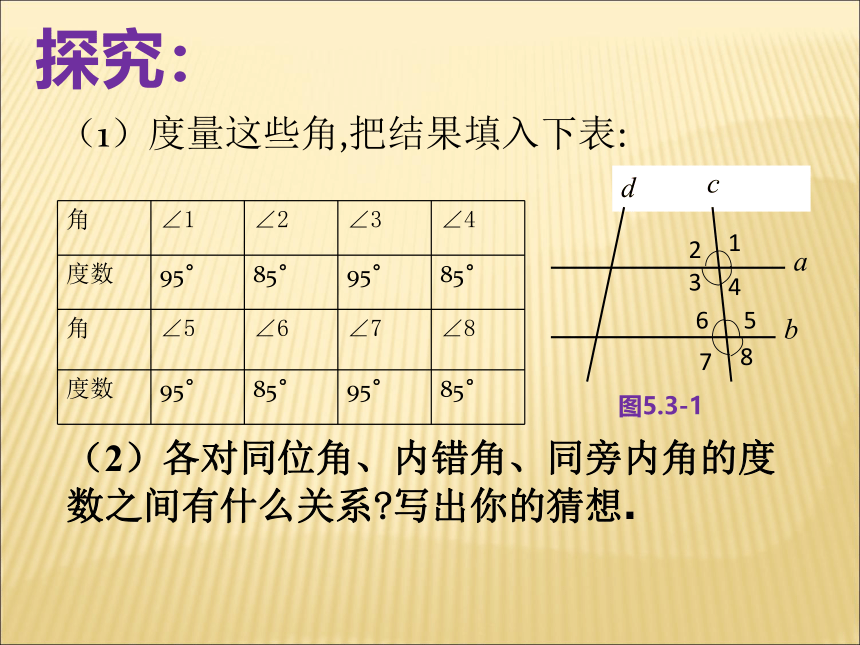
探究:
(1)度量这些角,把结果填入下表:
探究:
角
∠1
∠2
∠3
∠4
度数
95°
85°
95°
85°
角
∠5
∠6
∠7
∠8
度数
95°
85°
95°
85°
(2)各对同位角、内错角、同旁内角的度数之间有什么关系?写出你的猜想.
a
8
3
2
1
7
d
6
5
4
b
c
图5.3-1
两条平行线被第三条直线所截,
同位角____________,
内错角____________,
同旁内角___________.
相等
相等
互补
猜想:
a
8
3
2
1
7
d
6
5
4
b
c
两直线平行,同位角相等.
平行线的性质1
结论
两条平行线被第三条直线所截,
同位角相等.
性质发现
∴∠1=∠2.
∵a∥b,
简写为:
符号语言:
b
1
2
a
c
两直线平行,内错角相等.
平行线的性质2
结论
两条平行线被第三条直线所截,
内错角相等.
性质发现
∴∠2=∠3.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
3
两直线平行,同旁内角互补.
平行线的性质3
结论
两条平行线被第三条直线所截,
同旁内角互补.
性质发现
∴? 2+ ? 4=180°.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
4
性质1:两条平行线被第三条直线所截,同位角相等. (简单说成:两直线平行,同位角相等)
性质2:两条平行线被第三条直线所截,内错角相等. (简单说成:两直线平行,内错角相等)
性质3:两条平行线被第三条直线所截,同旁内角互补.(简单说成:两直线平行,同旁内角互补)
平行线的性质
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
例1: 小明不小心把家里的梯形玻璃块打碎了,还剩下梯形上底的一部分(如图).要订造一块新的玻璃,已经量得∠A=100°,∠B=105°,请你算一算:梯形另外两个角各是多少度?
解:因为梯形上.下底互相平行,
所以∠A与∠C互补,∠B与∠D互补.
于是∠C=180°-∠A
=180°-100°=80°,
∠D=180°-∠B
=180°-105°=75°.
答:梯形的另外两个 角分别是80°,75°.
A
B
C
D
图形
已知
结果
结论
同位角
内错角
同旁内角
两直线平行
同旁内角互补
1
2
)
)
a
b
c
2
3
)
)
a
b
c
2
4
)
)
a
b
c
平行线的性质
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
a//b
∠1=∠2
∠2=∠3
∠2+∠4=180°
课堂小结
作业布置
教科书:第21页练习第1、2题,
第23页习题5.3第2、3、4题.
内错角相等
同旁内角互补
两直线平行
平行线的判定方法有哪几种?
复习:
猜一猜∠1和∠2相等吗?
b
1
2
a
c
交流合作,探索发现
65°
65°
c
a
b
1
2
合作交流一
量一量
b
2
a
c
1
拼一拼
∠1=∠2
(1)度量这些角,把结果填入下表:
角
∠1
∠2
∠3
∠4
度数
角
∠5
∠6
∠7
∠8
度数
a
8
3
2
1
7
d
6
5
4
b
c
探究:
(1)度量这些角,把结果填入下表:
探究:
角
∠1
∠2
∠3
∠4
度数
95°
85°
95°
85°
角
∠5
∠6
∠7
∠8
度数
95°
85°
95°
85°
(2)各对同位角、内错角、同旁内角的度数之间有什么关系?写出你的猜想.
a
8
3
2
1
7
d
6
5
4
b
c
图5.3-1
两条平行线被第三条直线所截,
同位角____________,
内错角____________,
同旁内角___________.
相等
相等
互补
猜想:
a
8
3
2
1
7
d
6
5
4
b
c
两直线平行,同位角相等.
平行线的性质1
结论
两条平行线被第三条直线所截,
同位角相等.
性质发现
∴∠1=∠2.
∵a∥b,
简写为:
符号语言:
b
1
2
a
c
两直线平行,内错角相等.
平行线的性质2
结论
两条平行线被第三条直线所截,
内错角相等.
性质发现
∴∠2=∠3.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
3
两直线平行,同旁内角互补.
平行线的性质3
结论
两条平行线被第三条直线所截,
同旁内角互补.
性质发现
∴? 2+ ? 4=180°.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
4
性质1:两条平行线被第三条直线所截,同位角相等. (简单说成:两直线平行,同位角相等)
性质2:两条平行线被第三条直线所截,内错角相等. (简单说成:两直线平行,内错角相等)
性质3:两条平行线被第三条直线所截,同旁内角互补.(简单说成:两直线平行,同旁内角互补)
平行线的性质
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
例1: 小明不小心把家里的梯形玻璃块打碎了,还剩下梯形上底的一部分(如图).要订造一块新的玻璃,已经量得∠A=100°,∠B=105°,请你算一算:梯形另外两个角各是多少度?
解:因为梯形上.下底互相平行,
所以∠A与∠C互补,∠B与∠D互补.
于是∠C=180°-∠A
=180°-100°=80°,
∠D=180°-∠B
=180°-105°=75°.
答:梯形的另外两个 角分别是80°,75°.
A
B
C
D
图形
已知
结果
结论
同位角
内错角
同旁内角
两直线平行
同旁内角互补
1
2
)
)
a
b
c
2
3
)
)
a
b
c
2
4
)
)
a
b
c
平行线的性质
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
a//b
∠1=∠2
∠2=∠3
∠2+∠4=180°
课堂小结
作业布置
教科书:第21页练习第1、2题,
第23页习题5.3第2、3、4题.
