2020-2021学年人教版七年级数学下册教学课件-5.1.2垂线(16张)
文档属性
| 名称 | 2020-2021学年人教版七年级数学下册教学课件-5.1.2垂线(16张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-06 00:00:00 | ||
图片预览




文档简介
5.1.2 垂 线
1
1
学习目标:
1.学习垂线的定义,学会用几何的语言表示
2. 学习垂线的画法探究垂线的性质,
并会利用所 学知识进行简单的推理.
2
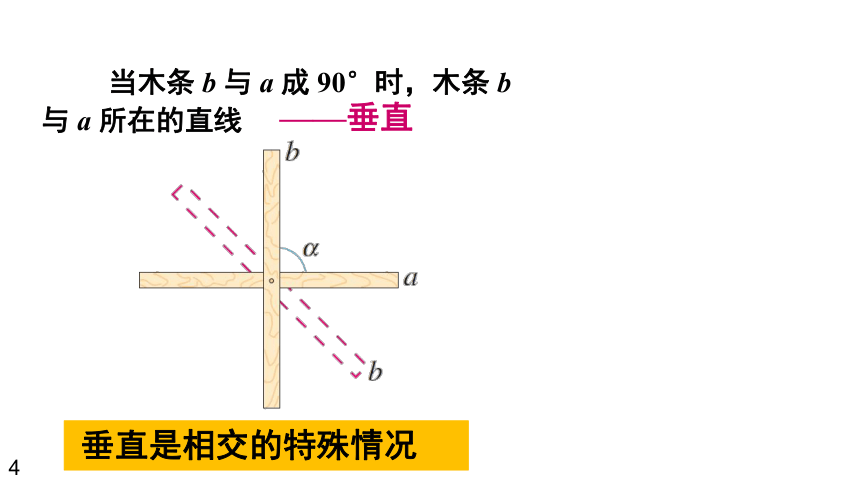
在相交线的模型中,固定木条 a ,转动木条 b.当b 的位置发生变化时,
a 与 b 所成的角a也随之发生改变。
3
当木条 b 与 a 成 90°时,木条 b 与 a 所在的直线
——垂直
垂直是相交的特殊情况
4
垂线的定义:当两条直线相交所成的四个角中有一个角是 90°时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,他们的交点叫做垂足
知识点1
记作: AB⊥CD,垂足为O或者AB⊥CD于点O
“⊥”读作“垂直于”
5
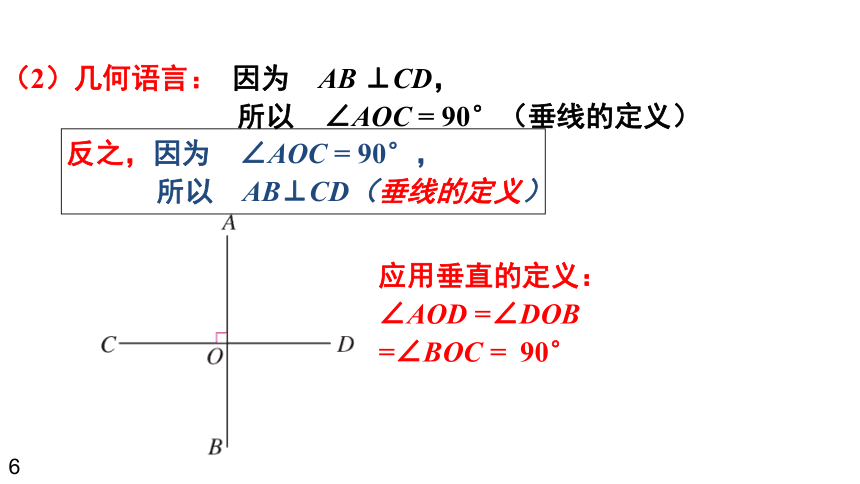
(2)几何语言: 因为 AB ⊥CD,
所以 ∠AOC = 90°(垂线的定义)
反之,因为 ∠AOC = 90°,
所以 AB⊥CD(垂线的定义)
6
应用垂直的定义:
∠AOD =∠DOB
=∠BOC = 90°
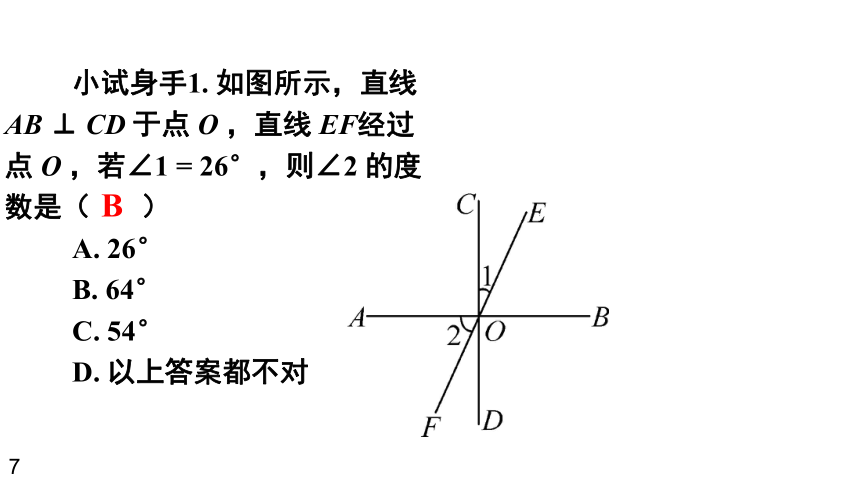
小试身手1. 如图所示,直线 AB ⊥ CD 于点 O ,直线 EF经过点 O ,若∠1 = 26°,则∠2 的度数是( )
A. 26°
B. 64°
C. 54°
D. 以上答案都不对
B
7
用三角尺或量角器画已知直线 l 的垂线.(1)用三角尺或量角器画已知直线 l 的垂线,这样的垂线能画出几条?
无数条
知识点2
垂线的画法
l
8
(2)经过一点画已知直线 l 的垂线,这样的垂线能画出几条?
① 该点和已知直线 l 有几种位置关系?
② 通过画图,你发现过一个点可以画几条直线与已知直线垂直?
2 种,
点在直线上和点在直线外
l
l
A
9
垂线性质:在同一平面内,过一点有且只有一条直线与已知直线垂直.
P
l
P
l
10
A
B
1.过点 P 画出射线 AB 的垂线.
练习
P
(1)
11
A
B
P
(2)
过点 P 画出线段 AB 的垂线.
12
基础巩固
1. 如图所示,若 AB ⊥ CD 于点 O ,则∠AOD = _____;若∠BOD = 90°,则 AB _____ CD.
90°
⊥
13
2.下列说法正确的有( )
①两条直线相交,交点叫做垂足;
②在同一平面内,过一点有且只有一条直线
与已知直线垂直;
③在同一平面内,一条直线有且只有一条垂线;
④在同一平面内,一条线段有无数条垂线;
⑤过一点不可能向一条射线或线段作垂线;
⑥若l1⊥l2,则l1是 l2的垂线,l2不是 l1的垂线. A.2个 B.3个 C.4个 D.5个
A
14
垂线
定义
画法
当两条直线相交所成的四个角中有一个角为 90°时,这两条直线互相垂直, 其中一条直线叫做另一条直线的垂线
利用三角尺或量角器画:1放、2移、3画线
16
谢 谢 观 看 !
16
17
1
1
学习目标:
1.学习垂线的定义,学会用几何的语言表示
2. 学习垂线的画法探究垂线的性质,
并会利用所 学知识进行简单的推理.
2
在相交线的模型中,固定木条 a ,转动木条 b.当b 的位置发生变化时,
a 与 b 所成的角a也随之发生改变。
3
当木条 b 与 a 成 90°时,木条 b 与 a 所在的直线
——垂直
垂直是相交的特殊情况
4
垂线的定义:当两条直线相交所成的四个角中有一个角是 90°时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,他们的交点叫做垂足
知识点1
记作: AB⊥CD,垂足为O或者AB⊥CD于点O
“⊥”读作“垂直于”
5
(2)几何语言: 因为 AB ⊥CD,
所以 ∠AOC = 90°(垂线的定义)
反之,因为 ∠AOC = 90°,
所以 AB⊥CD(垂线的定义)
6
应用垂直的定义:
∠AOD =∠DOB
=∠BOC = 90°
小试身手1. 如图所示,直线 AB ⊥ CD 于点 O ,直线 EF经过点 O ,若∠1 = 26°,则∠2 的度数是( )
A. 26°
B. 64°
C. 54°
D. 以上答案都不对
B
7
用三角尺或量角器画已知直线 l 的垂线.(1)用三角尺或量角器画已知直线 l 的垂线,这样的垂线能画出几条?
无数条
知识点2
垂线的画法
l
8
(2)经过一点画已知直线 l 的垂线,这样的垂线能画出几条?
① 该点和已知直线 l 有几种位置关系?
② 通过画图,你发现过一个点可以画几条直线与已知直线垂直?
2 种,
点在直线上和点在直线外
l
l
A
9
垂线性质:在同一平面内,过一点有且只有一条直线与已知直线垂直.
P
l
P
l
10
A
B
1.过点 P 画出射线 AB 的垂线.
练习
P
(1)
11
A
B
P
(2)
过点 P 画出线段 AB 的垂线.
12
基础巩固
1. 如图所示,若 AB ⊥ CD 于点 O ,则∠AOD = _____;若∠BOD = 90°,则 AB _____ CD.
90°
⊥
13
2.下列说法正确的有( )
①两条直线相交,交点叫做垂足;
②在同一平面内,过一点有且只有一条直线
与已知直线垂直;
③在同一平面内,一条直线有且只有一条垂线;
④在同一平面内,一条线段有无数条垂线;
⑤过一点不可能向一条射线或线段作垂线;
⑥若l1⊥l2,则l1是 l2的垂线,l2不是 l1的垂线. A.2个 B.3个 C.4个 D.5个
A
14
垂线
定义
画法
当两条直线相交所成的四个角中有一个角为 90°时,这两条直线互相垂直, 其中一条直线叫做另一条直线的垂线
利用三角尺或量角器画:1放、2移、3画线
16
谢 谢 观 看 !
16
17
