人教版八年级数学下册课件-18.2.2 菱形 菱形的性质(21张 含视频)
文档属性
| 名称 | 人教版八年级数学下册课件-18.2.2 菱形 菱形的性质(21张 含视频) |  | |
| 格式 | pptx | ||
| 文件大小 | 13.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-06 21:01:17 | ||
图片预览



文档简介
课题:菱形的性质
难点:菱形性质的应用
人教版八年级下册18.2.2
理解掌握菱形的定义及其性质
会用性质进行有关的证明和计算
会计算菱形的面积
教学目标
菱形的定义
有一组 的 叫做
邻边相等
平行四边形
A
D
C
B
几何语言:
∵四边形ABCD是平行四边形
AB=BC
∴四边形ABCD是 菱形
菱形
菱形的定义
自主学习
菱形的对角线互相垂直
菱形的每条对角线平分一组对角
角
猜想:菱形的性质
对角线
边
菱形的四条边相等
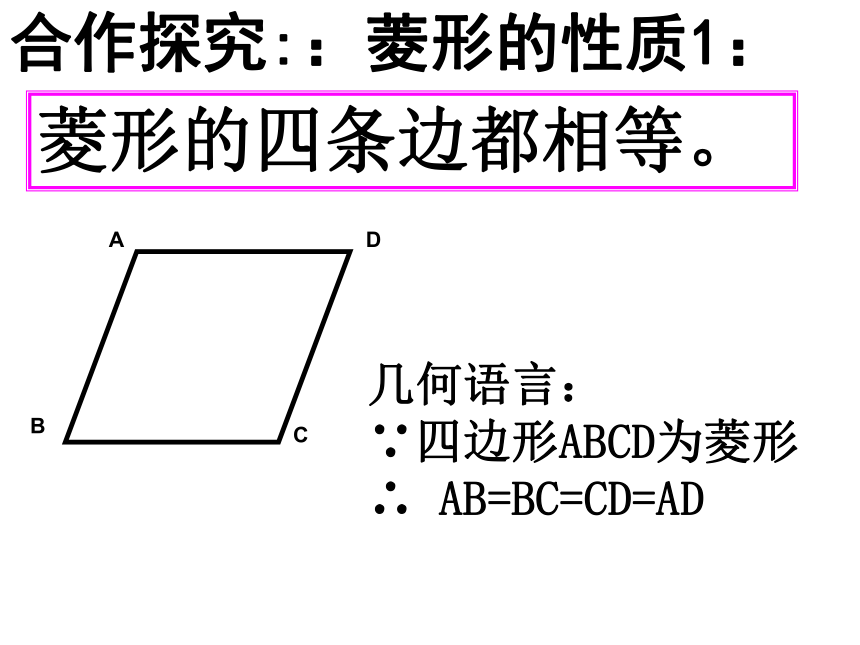
菱形的四条边都相等。
A
B
D
C
合作探究::菱形的性质1:
几何语言:
∵四边形ABCD为菱形
∴ AB=BC=CD=AD
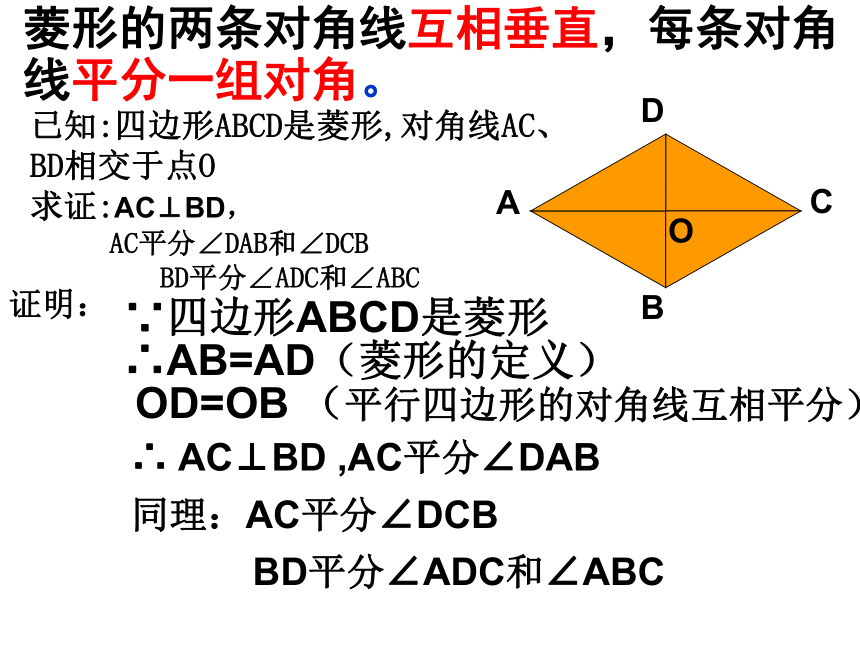
菱形的两条对角线互相垂直,每条对角线平分一组对角。
已知:四边形ABCD是菱形,对角线AC、BD相交于点O
求证:AC⊥BD,
AC平分∠DAB和∠DCB
BD平分∠ADC和∠ABC
证明:
O
C
B
D
O
A
∵四边形ABCD是菱形
∴AB=AD(菱形的定义)
OD=OB (平行四边形的对角线互相平分)
∴ AC⊥BD ,AC平分∠DAB
同理:AC平分∠DCB
BD平分∠ADC和∠ABC
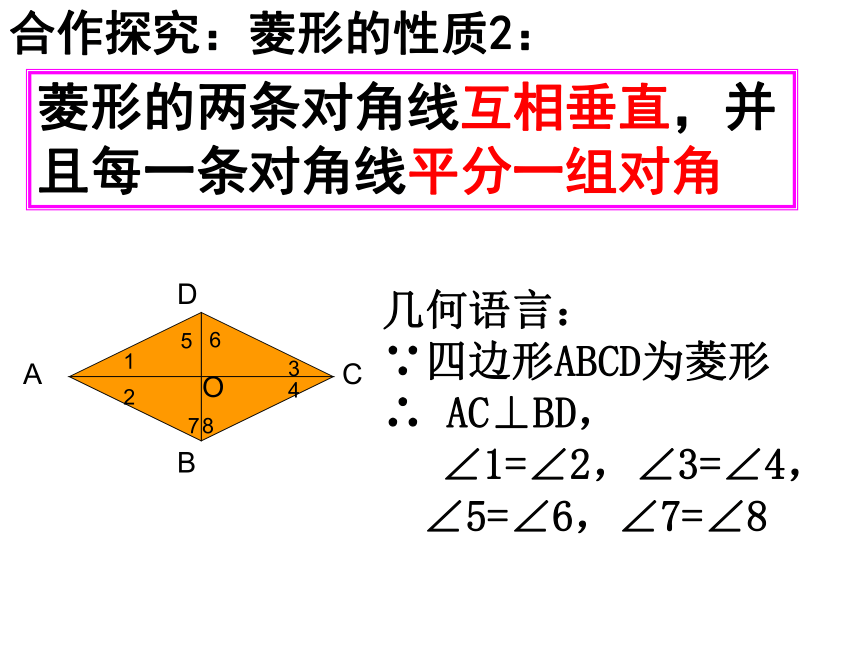
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角
合作探究:菱形的性质2:
几何语言:
∵四边形ABCD为菱形
∴ AC⊥BD,
∠1=∠2,∠3=∠4, ∠5=∠6,∠7=∠8
A
D
C
B
O
1
2
3
4
5
6
7
8
相等的线段:
相等的角:
等腰三角形有:
直角三角形有:
全等三角形有:
AB=CD=AD=BC
OA=OC OB=OD
∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8
△ABC △ DBC △ACD △ABD
Rt△AOB Rt△BOC Rt△COD Rt△DOA
Rt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACD
D
A
B
C
D
O
1
2
3
4
5
6
7
8
菱形的对角线互相垂直
菱形的每条对角线平分一组对角
角
菱形的性质
对角线
边
菱形的四条边相等
对称性
菱形既是轴对称图形又是中心对称图形
1.已知菱形的周长是12cm,那么它的边长是______.
2.菱形ABCD中∠ABC=60°,则∠BAC=_____。
3cm
60°
牛刀小试
3.菱形ABCD两条对角线BD、AC长分别是6cm和8cm,求菱形的边长和面积。
C
B
D
A
O
分析:
菱形的面积公式
C
B
D
A
O
E
S菱形=底×高=对角线乘积的一半
S菱形=
一个定义:
两个公式:
四个特性:
有一组邻边相等的平行四边形叫菱形
S菱形=底×高
S菱形= 对角线乘积的一半
“边、角、对角线、对称性”
课堂小结
课堂检测:
1.菱形的定义:有一组邻边_________的平行四边形
2.菱形的性质:
(1)边:菱形的四条边都________
(2)对角线:菱形的对角线互相____________ , 并且每一条对角线平分________对角。
3.菱形的面积:
(1)若菱形的边长为a,一边上的高为h,则
(2)若菱形的两条对角线的长分别为m,n,则
____________
____________
夯实基础
4.已知菱形的周长为20cm,那么它的边长是_______.
5.已知菱形的两条对角线长分别为2cm,3cm,则它的面积是_____
百炼成钢
6.如图,四边形ABCD是菱形∠ACD=30°,则∠BCD=_____∠ADC=_____
C
B
D
A
O
课堂检测:
1.菱形的定义:有一组邻边_________的平行四边形
2.菱形的性质:
(1)边:菱形的四条边都________
(2)对角线:菱形的对角线互相____________ , 并且每一条对角线平分________对角。
3.菱形的面积:
(1)若菱形的边长为a,一边上的高为h,则
(2)若菱形的两条对角线的长分别为m,n,则
____________
____________
相等
相等
垂直
一组
ah
mn
夯实基础
4.已知菱形的周长为20cm,那么它的边长是_______.
5.已知菱形的两条对角线长分别为2cm,3cm,则它的面积是_____
百炼成钢
6.如图,四边形ABCD是菱形∠ACD=30°,则∠BCD=_____∠ADC=_____
C
B
D
A
O
5cm
3
60°
120°
谢谢指导!
难点:菱形性质的应用
人教版八年级下册18.2.2
理解掌握菱形的定义及其性质
会用性质进行有关的证明和计算
会计算菱形的面积
教学目标
菱形的定义
有一组 的 叫做
邻边相等
平行四边形
A
D
C
B
几何语言:
∵四边形ABCD是平行四边形
AB=BC
∴四边形ABCD是 菱形
菱形
菱形的定义
自主学习
菱形的对角线互相垂直
菱形的每条对角线平分一组对角
角
猜想:菱形的性质
对角线
边
菱形的四条边相等
菱形的四条边都相等。
A
B
D
C
合作探究::菱形的性质1:
几何语言:
∵四边形ABCD为菱形
∴ AB=BC=CD=AD
菱形的两条对角线互相垂直,每条对角线平分一组对角。
已知:四边形ABCD是菱形,对角线AC、BD相交于点O
求证:AC⊥BD,
AC平分∠DAB和∠DCB
BD平分∠ADC和∠ABC
证明:
O
C
B
D
O
A
∵四边形ABCD是菱形
∴AB=AD(菱形的定义)
OD=OB (平行四边形的对角线互相平分)
∴ AC⊥BD ,AC平分∠DAB
同理:AC平分∠DCB
BD平分∠ADC和∠ABC
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角
合作探究:菱形的性质2:
几何语言:
∵四边形ABCD为菱形
∴ AC⊥BD,
∠1=∠2,∠3=∠4, ∠5=∠6,∠7=∠8
A
D
C
B
O
1
2
3
4
5
6
7
8
相等的线段:
相等的角:
等腰三角形有:
直角三角形有:
全等三角形有:
AB=CD=AD=BC
OA=OC OB=OD
∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8
△ABC △ DBC △ACD △ABD
Rt△AOB Rt△BOC Rt△COD Rt△DOA
Rt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACD
D
A
B
C
D
O
1
2
3
4
5
6
7
8
菱形的对角线互相垂直
菱形的每条对角线平分一组对角
角
菱形的性质
对角线
边
菱形的四条边相等
对称性
菱形既是轴对称图形又是中心对称图形
1.已知菱形的周长是12cm,那么它的边长是______.
2.菱形ABCD中∠ABC=60°,则∠BAC=_____。
3cm
60°
牛刀小试
3.菱形ABCD两条对角线BD、AC长分别是6cm和8cm,求菱形的边长和面积。
C
B
D
A
O
分析:
菱形的面积公式
C
B
D
A
O
E
S菱形=底×高=对角线乘积的一半
S菱形=
一个定义:
两个公式:
四个特性:
有一组邻边相等的平行四边形叫菱形
S菱形=底×高
S菱形= 对角线乘积的一半
“边、角、对角线、对称性”
课堂小结
课堂检测:
1.菱形的定义:有一组邻边_________的平行四边形
2.菱形的性质:
(1)边:菱形的四条边都________
(2)对角线:菱形的对角线互相____________ , 并且每一条对角线平分________对角。
3.菱形的面积:
(1)若菱形的边长为a,一边上的高为h,则
(2)若菱形的两条对角线的长分别为m,n,则
____________
____________
夯实基础
4.已知菱形的周长为20cm,那么它的边长是_______.
5.已知菱形的两条对角线长分别为2cm,3cm,则它的面积是_____
百炼成钢
6.如图,四边形ABCD是菱形∠ACD=30°,则∠BCD=_____∠ADC=_____
C
B
D
A
O
课堂检测:
1.菱形的定义:有一组邻边_________的平行四边形
2.菱形的性质:
(1)边:菱形的四条边都________
(2)对角线:菱形的对角线互相____________ , 并且每一条对角线平分________对角。
3.菱形的面积:
(1)若菱形的边长为a,一边上的高为h,则
(2)若菱形的两条对角线的长分别为m,n,则
____________
____________
相等
相等
垂直
一组
ah
mn
夯实基础
4.已知菱形的周长为20cm,那么它的边长是_______.
5.已知菱形的两条对角线长分别为2cm,3cm,则它的面积是_____
百炼成钢
6.如图,四边形ABCD是菱形∠ACD=30°,则∠BCD=_____∠ADC=_____
C
B
D
A
O
5cm
3
60°
120°
谢谢指导!
