人教版八年级下数学第19章一次函数单元复习课课件(18张)
文档属性
| 名称 | 人教版八年级下数学第19章一次函数单元复习课课件(18张) |  | |
| 格式 | ppt | ||
| 文件大小 | 366.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-06 21:03:01 | ||
图片预览






文档简介
一次函数复习课
变化的量是 .
1.试用含t的式子表示S .
没变化的量是 .
一辆汽车以60千米/小时的速度匀速行 驶,行驶里程为S千米,行驶时间为t小时.
2.在以上这个过程中,
里程S与时间t
速度60
S=60t
情景引入
一.常量、变量:
在一个变化过程中,数值发生变化的量叫做 变量;数值始终不变的量叫做 常量 ;
二、函数的概念:
一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
知识梳理
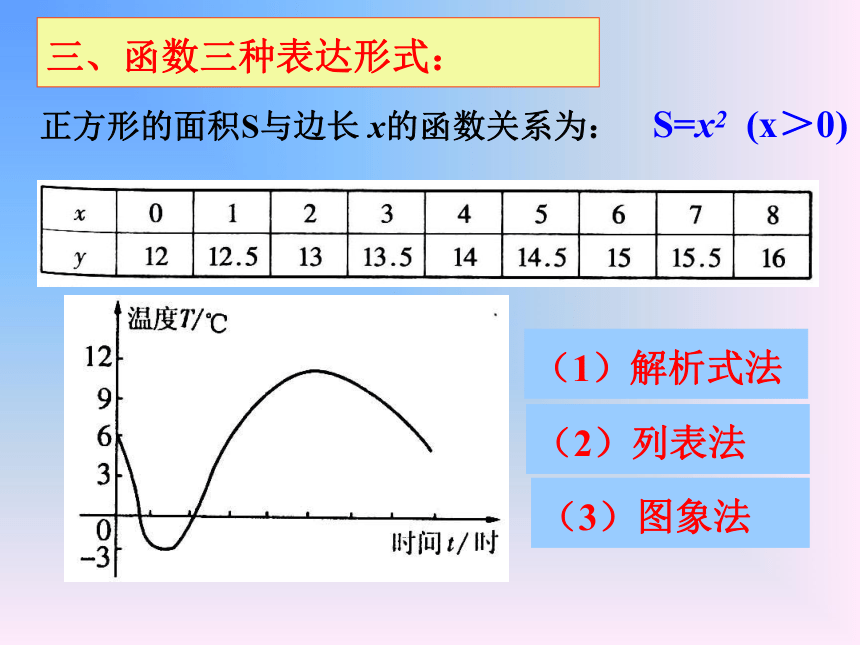
(1)解析式法
(2)列表法
(3)图象法
正方形的面积S与边长 x的函数关系为:
S=x2
(x>0)
三、函数三种表达形式:
1、列表(表中给出一些自变量的值及其对应的函数值。)
2、描点:(在直角坐标系中,以自变量的值为横坐
标,相应的函数值为纵坐标,描出表格中数值对应的
各点。
3、连线:(按照横坐标由小到大的顺序把所描的各点
用平滑的曲线连接起来)。
四、描点法画函数图象的步骤:
五、正比例函数与一次函数的概念:
当b =0 时,y=kx+b 即为正比例函数 y=kx,
所以正比例函数,是一次函数的特例.
一般地,形如y=kx+b(k,b为常数,且k≠0)的函数叫做一次函数.
注意:(1)k≠0 (2)X的次数是“1”
应用拓展
一、观察图形并判别K和b的符号,并说出理由
K>0,b>0
K>0,b=0
K>0,b<0
K<0,b=0
K<0,b>0
K<0,b<0
当k>0时,直线过一、三象限,y随x的增大而增大。
当k<0时,直线过二、四象限,y随x的增大而减小。
当b>0时,图象与y轴正半轴相交。过一、二象限。
当b<0时,图象与y轴负半轴相交。过三、四象限。
合作探究
1、直线y=kx+b经过一、二、四象限,则
K 0, b 0.
<
>
此时,直线y=bx+k的图象只能是( )
D
试一试:
二、观察图形,你能从图形中得到什么信息?能否利用这个信息求得该直线的函数解析式?
解:设函数解析式为y=kx+b(k≠0)
∵直线经过(4 ,0)与(0 ,2)点,则
●
●
如何求两条直线交点坐标?
两直线解析式联立方程组,方程组的解即为交点坐标。
三、请同学们在刚才图象上画出一次函数
的图象
B
(1,1.5)
四、
请问?
(1,1.5)
注:1、先看交点 2再看交点左右的图象高低。
一、老师如果给每个交点标出字母,你能否求得四边形OABC的面积?
方法一:利用大三角形减小三角形
方法二:把四边形分割成梯形和三角形
方法三:把四边形分割成两个小三角形
(-2,0)
(4,0)
(0,1)
(0,2)
(1,1.5)
能力提升
解:由图可知A(4,0),B(1,1.5),
C(0,1 ),D(0,2)
二、在直线 上是否存在着点p,使 △AOP的面积等于四边形OABC的面积?
(1,1.5)
. p
. p
⑴一次函数的定义、图像及基本性质
(2)待定系数法求函数解析式
(3)一次函数与二元一次方程组
(5)一次函数与图形的面积
(4)一次函数与不等式
归纳与小结
作 业
1.若一次函数y=x+b的图象过点A(1,-1), 则b=____
2.根据如图所示的条件,求直线的表达式。
3. 已知一次函数与某个正比例函数的图象交于A(2,4)点,该一次函数与x轴交于B点,O是坐标原点,且S△OAB=12,求正比例函数和一次函数的解析式.
必做题
选做题
共勉
幸福不会平白无故从天而降,
付出努力才会有补偿.
没有人能随随便便就辉煌,
除非只是好梦一场。
心中有梦想就要一如既往,
不能遇到困难说放就放.
千锤百炼才能磨炼出好钢.
饱经风霜才能更强。
变化的量是 .
1.试用含t的式子表示S .
没变化的量是 .
一辆汽车以60千米/小时的速度匀速行 驶,行驶里程为S千米,行驶时间为t小时.
2.在以上这个过程中,
里程S与时间t
速度60
S=60t
情景引入
一.常量、变量:
在一个变化过程中,数值发生变化的量叫做 变量;数值始终不变的量叫做 常量 ;
二、函数的概念:
一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
知识梳理
(1)解析式法
(2)列表法
(3)图象法
正方形的面积S与边长 x的函数关系为:
S=x2
(x>0)
三、函数三种表达形式:
1、列表(表中给出一些自变量的值及其对应的函数值。)
2、描点:(在直角坐标系中,以自变量的值为横坐
标,相应的函数值为纵坐标,描出表格中数值对应的
各点。
3、连线:(按照横坐标由小到大的顺序把所描的各点
用平滑的曲线连接起来)。
四、描点法画函数图象的步骤:
五、正比例函数与一次函数的概念:
当b =0 时,y=kx+b 即为正比例函数 y=kx,
所以正比例函数,是一次函数的特例.
一般地,形如y=kx+b(k,b为常数,且k≠0)的函数叫做一次函数.
注意:(1)k≠0 (2)X的次数是“1”
应用拓展
一、观察图形并判别K和b的符号,并说出理由
K>0,b>0
K>0,b=0
K>0,b<0
K<0,b=0
K<0,b>0
K<0,b<0
当k>0时,直线过一、三象限,y随x的增大而增大。
当k<0时,直线过二、四象限,y随x的增大而减小。
当b>0时,图象与y轴正半轴相交。过一、二象限。
当b<0时,图象与y轴负半轴相交。过三、四象限。
合作探究
1、直线y=kx+b经过一、二、四象限,则
K 0, b 0.
<
>
此时,直线y=bx+k的图象只能是( )
D
试一试:
二、观察图形,你能从图形中得到什么信息?能否利用这个信息求得该直线的函数解析式?
解:设函数解析式为y=kx+b(k≠0)
∵直线经过(4 ,0)与(0 ,2)点,则
●
●
如何求两条直线交点坐标?
两直线解析式联立方程组,方程组的解即为交点坐标。
三、请同学们在刚才图象上画出一次函数
的图象
B
(1,1.5)
四、
请问?
(1,1.5)
注:1、先看交点 2再看交点左右的图象高低。
一、老师如果给每个交点标出字母,你能否求得四边形OABC的面积?
方法一:利用大三角形减小三角形
方法二:把四边形分割成梯形和三角形
方法三:把四边形分割成两个小三角形
(-2,0)
(4,0)
(0,1)
(0,2)
(1,1.5)
能力提升
解:由图可知A(4,0),B(1,1.5),
C(0,1 ),D(0,2)
二、在直线 上是否存在着点p,使 △AOP的面积等于四边形OABC的面积?
(1,1.5)
. p
. p
⑴一次函数的定义、图像及基本性质
(2)待定系数法求函数解析式
(3)一次函数与二元一次方程组
(5)一次函数与图形的面积
(4)一次函数与不等式
归纳与小结
作 业
1.若一次函数y=x+b的图象过点A(1,-1), 则b=____
2.根据如图所示的条件,求直线的表达式。
3. 已知一次函数与某个正比例函数的图象交于A(2,4)点,该一次函数与x轴交于B点,O是坐标原点,且S△OAB=12,求正比例函数和一次函数的解析式.
必做题
选做题
共勉
幸福不会平白无故从天而降,
付出努力才会有补偿.
没有人能随随便便就辉煌,
除非只是好梦一场。
心中有梦想就要一如既往,
不能遇到困难说放就放.
千锤百炼才能磨炼出好钢.
饱经风霜才能更强。
