人教版八年级下册数学19.2.3一次函数与一元一次不等式课件(24张)
文档属性
| 名称 | 人教版八年级下册数学19.2.3一次函数与一元一次不等式课件(24张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-06 21:04:48 | ||
图片预览



文档简介
一次函数与不等式
引入
已知一次函数y=2x+2,求满足下列条件时自变量的取值
(1)函数值为0
(2)函数值为2
(3)函数值为4
(4)函数值为m
{5940675A-B579-460E-94D1-54222C63F5DA}一元一次方程的解
函数
“数”
“形”
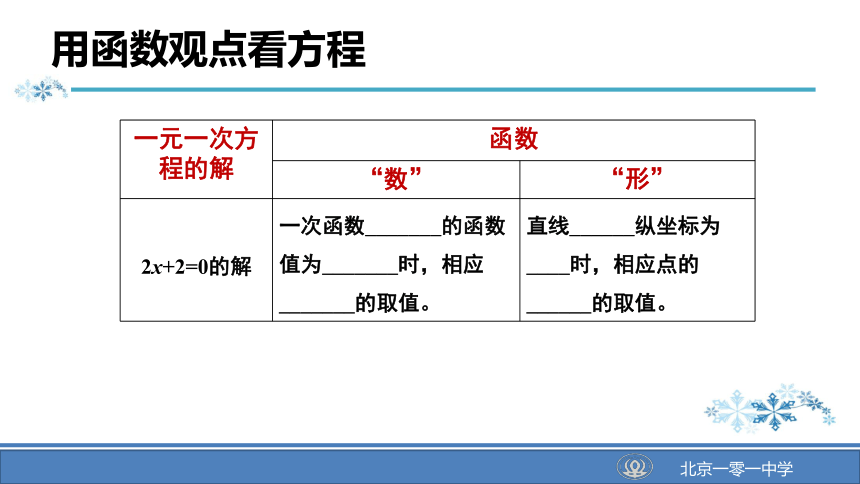
2x+2=0的解
一次函数_______的函数值为_______时,相应_______的取值。
直线______纵坐标为____时,相应点的______的取值。
用函数观点看方程
{5940675A-B579-460E-94D1-54222C63F5DA}一元一次方程的解
函数
“数”
“形”
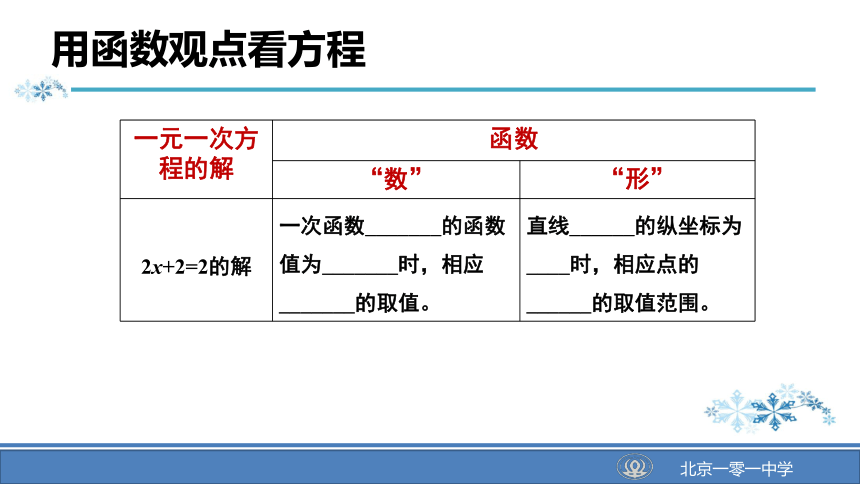
2x+2=2的解
一次函数_______的函数值为_______时,相应_______的取值。
直线______的纵坐标为____时,相应点的______的取值范围。
用函数观点看方程
{5940675A-B579-460E-94D1-54222C63F5DA}一元一次方程的解
函数
“数”
“形”
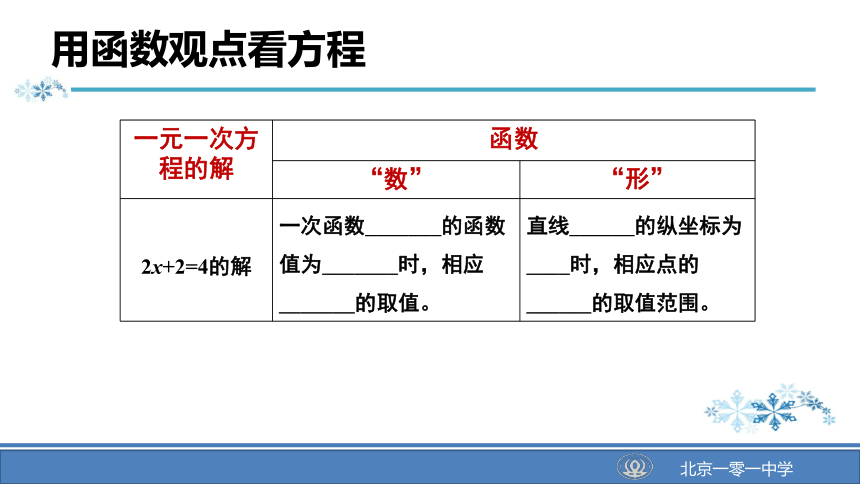
2x+2=4的解
一次函数_______的函数值为_______时,相应_______的取值。
直线______的纵坐标为____时,相应点的______的取值范围。
用函数观点看方程
{5940675A-B579-460E-94D1-54222C63F5DA}一元一次方程的解
函数
“数”
“形”
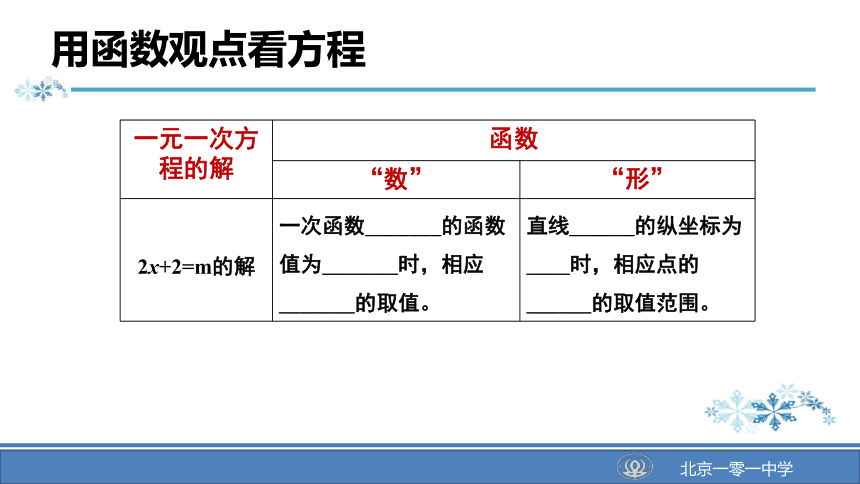
2x+2=m的解
一次函数_______的函数值为_______时,相应_______的取值。
直线______的纵坐标为____时,相应点的______的取值范围。
用函数观点看方程
已知一次函数y=2x+2,求满足下列条件时自变量的取值
(1)函数值小于0
(2)函数值不小于2
(3)函数值大于4
(4)函数值不大于m
{5940675A-B579-460E-94D1-54222C63F5DA}一元一次不等式的解集
函数
“数”
“形”
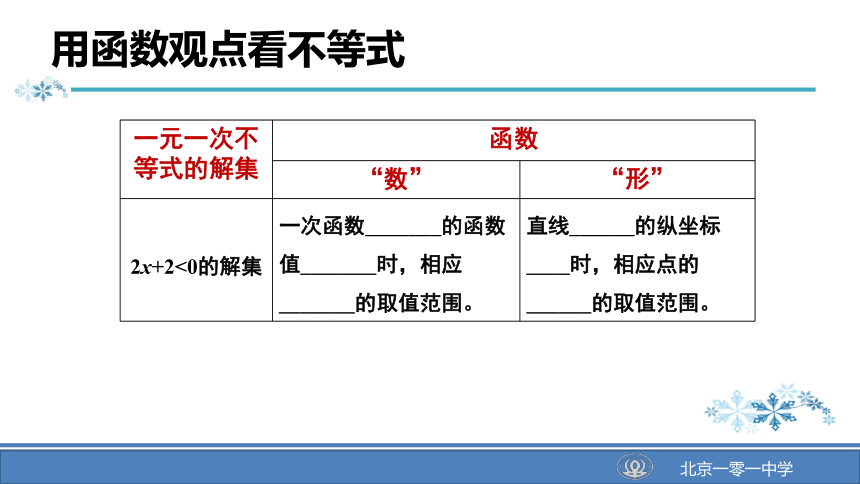
2x+2<0的解集
一次函数_______的函数值_______时,相应_______的取值范围。
直线______的纵坐标____时,相应点的______的取值范围。
用函数观点看不等式
{5940675A-B579-460E-94D1-54222C63F5DA}一元一次不等式的解
函数
“数”
“形”
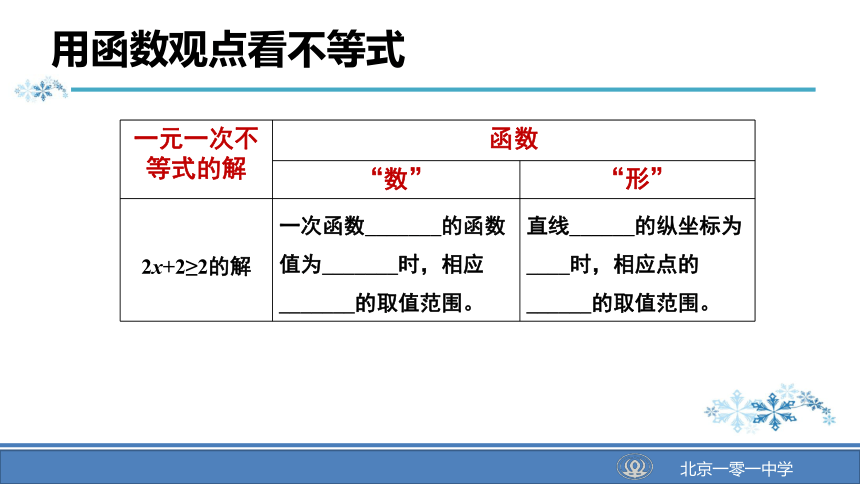
2x+2≥2的解
一次函数_______的函数值为_______时,相应_______的取值范围。
直线______的纵坐标为____时,相应点的______的取值范围。
用函数观点看不等式
{5940675A-B579-460E-94D1-54222C63F5DA}一元一次不等式的解
函数
“数”
“形”
2x+2>4的解集
一次函数_______的函数值为_______时,相应_______的取值范围。
直线______的纵坐标为____时,相应点的______的取值范围。
用函数观点看不等式
{5940675A-B579-460E-94D1-54222C63F5DA}一元一次不等式的解
函数
“数”
“形”
2x+2≤m的解集
一次函数_______的函数值为_______时,相应_______的取值范围。
直线______的纵坐标为____时,相应点的______的取值范围。
用函数观点看不等式
用函数观点, 解释不等式-x+3>1的解集?
任意一个一元一次不等式?
两个同学为一组,每人写一个一元一次不等式,另一个同学用函数观点对不等式的解集进行解释。
小组活动
用函数观点解释不等式
2x+2<-x+3的解集?
例1.已知右图为函数y=kx+b
的图象,则:
(1)不等式kx+b>4的解为____
(2)不等式kx+b<-1的解为___
知识应用
例1.已知右图为函数y=kx+b
的图象,则:
(3)不等式kx+b-4<0的解为____
(4)不等式kx+b+1>0的解为___
知识应用
例1.已知右图为函数y=kx+b
的图象,则:
(5)若 ,则y的取值范围为____
(6)若-1知识应用
知识应用
例2.函数y=x+b与y'=kx+3的图象如图所示,则
(1)不等式x+b>kx+3的解集为____
知识应用
例2.函数y=x+b与y'=kx+3的图象如图所示,则
(2)不等式x+b>kx+3>-1的解集为____
知识应用
例2.函数y=x+b与y'=kx+3的图象如图所示,则
(3)使得y与y'都大于零的x的取值范围是____
知识应用
例2.函数y=x+b与y'=kx+3的图象如图所示,则
(4)根据图象你能自己设计一道方程(组)或不等式(组)的题目吗?
小结
1.用函数的观点看不等式
2.注重数形结合的数学思想;
后续可研究的问题
不等式解集存在性的讨论;
不等式组有解和无解情况的讨论;
引入
已知一次函数y=2x+2,求满足下列条件时自变量的取值
(1)函数值为0
(2)函数值为2
(3)函数值为4
(4)函数值为m
{5940675A-B579-460E-94D1-54222C63F5DA}一元一次方程的解
函数
“数”
“形”
2x+2=0的解
一次函数_______的函数值为_______时,相应_______的取值。
直线______纵坐标为____时,相应点的______的取值。
用函数观点看方程
{5940675A-B579-460E-94D1-54222C63F5DA}一元一次方程的解
函数
“数”
“形”
2x+2=2的解
一次函数_______的函数值为_______时,相应_______的取值。
直线______的纵坐标为____时,相应点的______的取值范围。
用函数观点看方程
{5940675A-B579-460E-94D1-54222C63F5DA}一元一次方程的解
函数
“数”
“形”
2x+2=4的解
一次函数_______的函数值为_______时,相应_______的取值。
直线______的纵坐标为____时,相应点的______的取值范围。
用函数观点看方程
{5940675A-B579-460E-94D1-54222C63F5DA}一元一次方程的解
函数
“数”
“形”
2x+2=m的解
一次函数_______的函数值为_______时,相应_______的取值。
直线______的纵坐标为____时,相应点的______的取值范围。
用函数观点看方程
已知一次函数y=2x+2,求满足下列条件时自变量的取值
(1)函数值小于0
(2)函数值不小于2
(3)函数值大于4
(4)函数值不大于m
{5940675A-B579-460E-94D1-54222C63F5DA}一元一次不等式的解集
函数
“数”
“形”
2x+2<0的解集
一次函数_______的函数值_______时,相应_______的取值范围。
直线______的纵坐标____时,相应点的______的取值范围。
用函数观点看不等式
{5940675A-B579-460E-94D1-54222C63F5DA}一元一次不等式的解
函数
“数”
“形”
2x+2≥2的解
一次函数_______的函数值为_______时,相应_______的取值范围。
直线______的纵坐标为____时,相应点的______的取值范围。
用函数观点看不等式
{5940675A-B579-460E-94D1-54222C63F5DA}一元一次不等式的解
函数
“数”
“形”
2x+2>4的解集
一次函数_______的函数值为_______时,相应_______的取值范围。
直线______的纵坐标为____时,相应点的______的取值范围。
用函数观点看不等式
{5940675A-B579-460E-94D1-54222C63F5DA}一元一次不等式的解
函数
“数”
“形”
2x+2≤m的解集
一次函数_______的函数值为_______时,相应_______的取值范围。
直线______的纵坐标为____时,相应点的______的取值范围。
用函数观点看不等式
用函数观点, 解释不等式-x+3>1的解集?
任意一个一元一次不等式?
两个同学为一组,每人写一个一元一次不等式,另一个同学用函数观点对不等式的解集进行解释。
小组活动
用函数观点解释不等式
2x+2<-x+3的解集?
例1.已知右图为函数y=kx+b
的图象,则:
(1)不等式kx+b>4的解为____
(2)不等式kx+b<-1的解为___
知识应用
例1.已知右图为函数y=kx+b
的图象,则:
(3)不等式kx+b-4<0的解为____
(4)不等式kx+b+1>0的解为___
知识应用
例1.已知右图为函数y=kx+b
的图象,则:
(5)若 ,则y的取值范围为____
(6)若-1
知识应用
例2.函数y=x+b与y'=kx+3的图象如图所示,则
(1)不等式x+b>kx+3的解集为____
知识应用
例2.函数y=x+b与y'=kx+3的图象如图所示,则
(2)不等式x+b>kx+3>-1的解集为____
知识应用
例2.函数y=x+b与y'=kx+3的图象如图所示,则
(3)使得y与y'都大于零的x的取值范围是____
知识应用
例2.函数y=x+b与y'=kx+3的图象如图所示,则
(4)根据图象你能自己设计一道方程(组)或不等式(组)的题目吗?
小结
1.用函数的观点看不等式
2.注重数形结合的数学思想;
后续可研究的问题
不等式解集存在性的讨论;
不等式组有解和无解情况的讨论;
