人教版八年级数学下册课件-17.1 勾股定理(27张)
文档属性
| 名称 | 人教版八年级数学下册课件-17.1 勾股定理(27张) |  | |
| 格式 | ppt | ||
| 文件大小 | 780.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-06 21:04:43 | ||
图片预览





文档简介
勾股定理
学习目标
课堂导入
探索过程
巩固练习
课堂总结
课后作业
勾股定理
中国勾股
一、学习目标
1.了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
2.培养在实际生活中发现问题总结规律的意识和能力。?
3.介绍我国古代在勾股定理研究方面所取得的成就,激发学生的爱国热情,促其勤奋学习。
返回
2002年,在北京召开的国际数学家大会(TCM-2002),大会的会标图案就是“弦图”,“弦图”最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的. 它标志着中国古代的数学成就.
返回
毕达哥拉斯
他的发现
:
继续
A
B
C
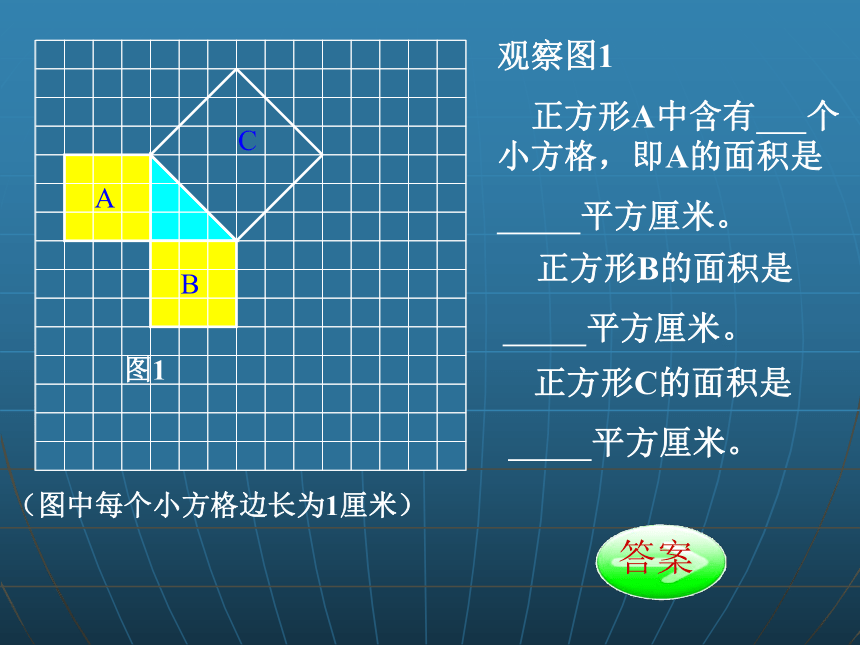
(图中每个小方格边长为1厘米)
图1
观察图1
正方形A中含有 个小方格,即A的面积是
平方厘米。
正方形B的面积是
平方厘米。
正方形C的面积是
平方厘米。
答案
A
B
C
(图中每个小方格边长为1厘米)
图1
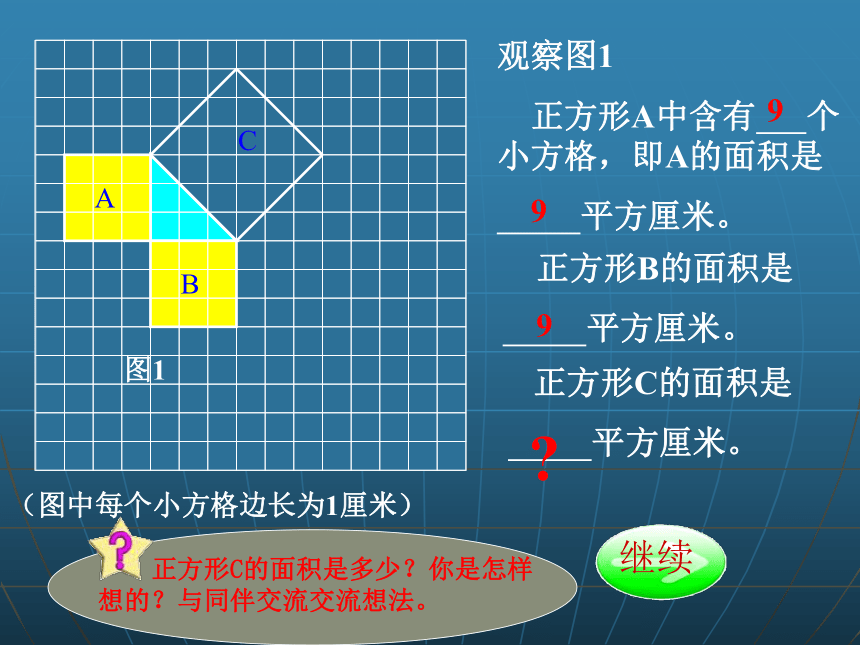
观察图1
正方形A中含有 个小方格,即A的面积是
平方厘米。
正方形B的面积是
平方厘米。
正方形C的面积是
平方厘米。
9
9
9
?
继续
正方形C的面积是多少?你是怎样想的?与同伴交流交流想法。
A
B
C
(图中每个小方格边长为1厘米)
图1
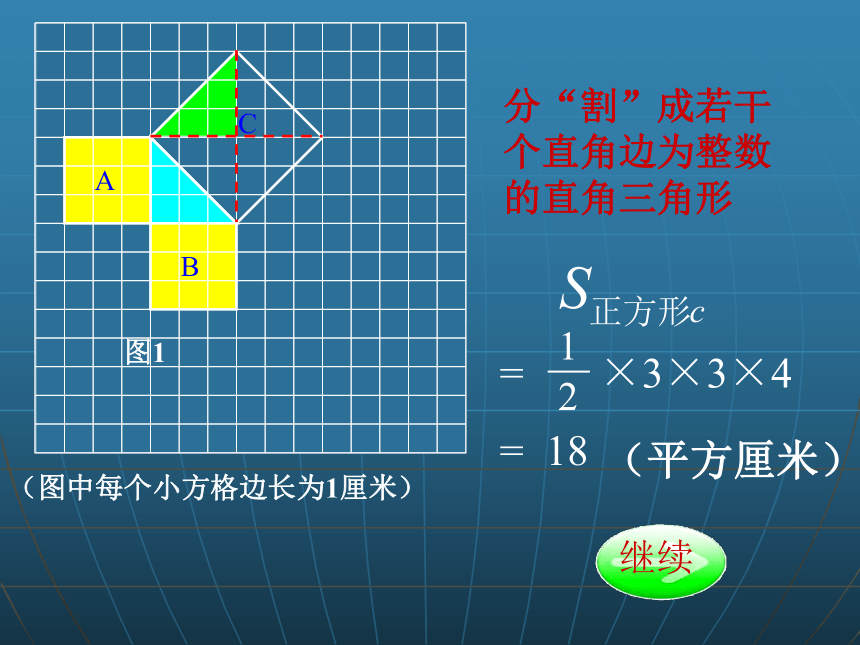
分“割”成若干个直角边为整数的直角三角形
(平方厘米)
c
S
正方形
= ×3×3×4
= 18
1
2
继续
A
B
C
(图中每个小方格边长为1厘米)
图1
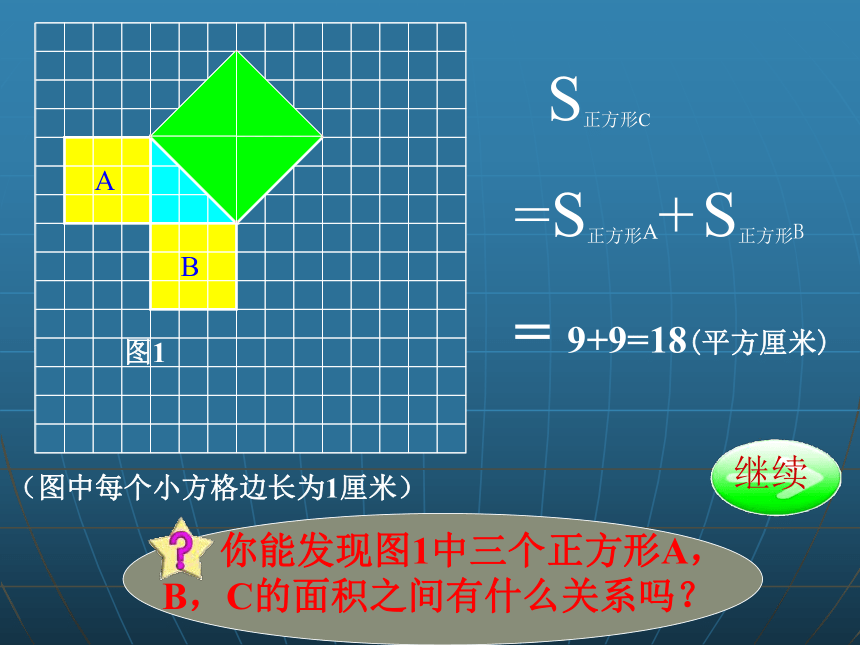
S正方形C
=S正方形A+ S正方形B
= 9+9=18(平方厘米)
你能发现图1中三个正方形A,B,C的面积之间有什么关系吗?
继续
A
B
C
(图中每个小方格边长为1厘米)
图1
你能发现图1中三个正方形A,B,C的面积之间有什么关系吗?
继续
SA+SB=SC
小结:等腰三角形两条直角边上的正方形面积之和等于斜边上的正方形的面积。
A
B
那么一般的直角三角形中,三条边为边所形成的正方形中,有这样的规律吗??
SA+SB=SC
A
B
图2
A
B
C
图3
C
继续
C
图2
SA+SB=SC
一般的直角三角形三边为边作正方形
c
S
正方形
= ×4×3×4+1
= 25
1
2
(平方厘米)
A
B
C
图2
继续
小组讨论:你能把正方形C分割成若干个直角边为整数的三角形,再求出它的面积吗?
怎样计算正方形C的面积呢??
A
B
C
图2
SA+SB=SC
一般的直角三角形三边为边作正方形
(平方厘米)
=16+9=25(平方厘米)
C
=S
正方形
=4×4
=16
A
S
正方形
(平方厘米)
=3×3
=9
B
S
正方形
B
S
正方形
+
A
S
正方形
C
继续
即:SA+SB=SC
C
SA+SB=SC
A
B
C
图2
议一议
(1)你能用三角形的边长表示正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流。
探究过程
A
B
C
a
c
b
SA+SB=SC
观察所得到的各组数据,你有什么发现?
猜想:两直角边a、b与斜边c 之间的关系?
即:a2+b2=c2
继续
┏
a2+b2=c2
a
c
b
直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
勾股定理
(毕达哥拉斯定理)
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.
继续
下面让我们一起推导勾股定理吧!
c
a
b
c
a
b
c
a
b
c
a
b
∵ c2=
=b2-2ab+a2+ 2ab
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
该图2002年8月在北京召开的国际数学家大会的会标示意图,取材于我国古代数学著作《勾股圆方图》。
勾股定理
证明1:
答案
求证过程
证法2
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 =
a2+2ab+b2 = 2ab +C2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
C2
C2
勾股定理
证明2:
答案
求证过程
a
b
c
a
b
c
a
b
c
b
a
c
b
a
c
b
c
a
b
c
a
b
c
a
证法3
a
b
c
b
a
c
A
B
C
D
E
这一证法称为“总统证法”
你能只用这两个直角三角形说明a2+b2=c2吗?
拼一拼 试一试
勾股定理
证明3:
求证过程
总统证法
1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。
1881年,伽菲尔德就任美国第20任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”。
返回
答案
P
625
400
2
6
x
P的面积 =______________
X=____________
225
B
A
C
AB=__________
AC=__________
BC=__________
25
15
20
做一做
1.
下一题
比一比看看谁算得快!
2.求下列直角三角形中未知边的长:
8
x
17
16
20
x
12
5
x
做一做
下一题
答案
1、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为 ( )
A.3 米 B.4 米 C.5米 D.6米
C
3
4
解决问题
下一题
答案
2、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为 ( )
A
B
C
A.50米 B.120米 C.100米 D.130米
130
120
?
A
解决问题
下一题
演示
如图,大风将一根木制旗杆吹裂,随时都可能倒下,十分危急。接警后“119”迅速赶到现场,并决定从断裂处将旗杆折断。现在需要划出一个安全警戒区域,那么你能确定这个安全区域的半径至少是多少米吗?
9m
24m
?
解决问题
下一题
拓展题:对比两个图形,你能直接观察验证出勾股定理吗?
两幅图中彩色的四个直角三角形总面积呢?
提示:图中的两个大正方形面积相等吗?
空白部分的面积呢?那剩余的
返回
课堂总结
①本节课学到了什么数学知识?
②你了解了勾股定理的发现方法了吗?
③你还有什么困惑?
返回
学习目标
课堂导入
探索过程
巩固练习
课堂总结
课后作业
勾股定理
中国勾股
一、学习目标
1.了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
2.培养在实际生活中发现问题总结规律的意识和能力。?
3.介绍我国古代在勾股定理研究方面所取得的成就,激发学生的爱国热情,促其勤奋学习。
返回
2002年,在北京召开的国际数学家大会(TCM-2002),大会的会标图案就是“弦图”,“弦图”最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的. 它标志着中国古代的数学成就.
返回
毕达哥拉斯
他的发现
:
继续
A
B
C
(图中每个小方格边长为1厘米)
图1
观察图1
正方形A中含有 个小方格,即A的面积是
平方厘米。
正方形B的面积是
平方厘米。
正方形C的面积是
平方厘米。
答案
A
B
C
(图中每个小方格边长为1厘米)
图1
观察图1
正方形A中含有 个小方格,即A的面积是
平方厘米。
正方形B的面积是
平方厘米。
正方形C的面积是
平方厘米。
9
9
9
?
继续
正方形C的面积是多少?你是怎样想的?与同伴交流交流想法。
A
B
C
(图中每个小方格边长为1厘米)
图1
分“割”成若干个直角边为整数的直角三角形
(平方厘米)
c
S
正方形
= ×3×3×4
= 18
1
2
继续
A
B
C
(图中每个小方格边长为1厘米)
图1
S正方形C
=S正方形A+ S正方形B
= 9+9=18(平方厘米)
你能发现图1中三个正方形A,B,C的面积之间有什么关系吗?
继续
A
B
C
(图中每个小方格边长为1厘米)
图1
你能发现图1中三个正方形A,B,C的面积之间有什么关系吗?
继续
SA+SB=SC
小结:等腰三角形两条直角边上的正方形面积之和等于斜边上的正方形的面积。
A
B
那么一般的直角三角形中,三条边为边所形成的正方形中,有这样的规律吗??
SA+SB=SC
A
B
图2
A
B
C
图3
C
继续
C
图2
SA+SB=SC
一般的直角三角形三边为边作正方形
c
S
正方形
= ×4×3×4+1
= 25
1
2
(平方厘米)
A
B
C
图2
继续
小组讨论:你能把正方形C分割成若干个直角边为整数的三角形,再求出它的面积吗?
怎样计算正方形C的面积呢??
A
B
C
图2
SA+SB=SC
一般的直角三角形三边为边作正方形
(平方厘米)
=16+9=25(平方厘米)
C
=S
正方形
=4×4
=16
A
S
正方形
(平方厘米)
=3×3
=9
B
S
正方形
B
S
正方形
+
A
S
正方形
C
继续
即:SA+SB=SC
C
SA+SB=SC
A
B
C
图2
议一议
(1)你能用三角形的边长表示正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流。
探究过程
A
B
C
a
c
b
SA+SB=SC
观察所得到的各组数据,你有什么发现?
猜想:两直角边a、b与斜边c 之间的关系?
即:a2+b2=c2
继续
┏
a2+b2=c2
a
c
b
直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
勾股定理
(毕达哥拉斯定理)
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.
继续
下面让我们一起推导勾股定理吧!
c
a
b
c
a
b
c
a
b
c
a
b
∵ c2=
=b2-2ab+a2+ 2ab
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
该图2002年8月在北京召开的国际数学家大会的会标示意图,取材于我国古代数学著作《勾股圆方图》。
勾股定理
证明1:
答案
求证过程
证法2
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 =
a2+2ab+b2 = 2ab +C2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
C2
C2
勾股定理
证明2:
答案
求证过程
a
b
c
a
b
c
a
b
c
b
a
c
b
a
c
b
c
a
b
c
a
b
c
a
证法3
a
b
c
b
a
c
A
B
C
D
E
这一证法称为“总统证法”
你能只用这两个直角三角形说明a2+b2=c2吗?
拼一拼 试一试
勾股定理
证明3:
求证过程
总统证法
1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。
1881年,伽菲尔德就任美国第20任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”。
返回
答案
P
625
400
2
6
x
P的面积 =______________
X=____________
225
B
A
C
AB=__________
AC=__________
BC=__________
25
15
20
做一做
1.
下一题
比一比看看谁算得快!
2.求下列直角三角形中未知边的长:
8
x
17
16
20
x
12
5
x
做一做
下一题
答案
1、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为 ( )
A.3 米 B.4 米 C.5米 D.6米
C
3
4
解决问题
下一题
答案
2、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为 ( )
A
B
C
A.50米 B.120米 C.100米 D.130米
130
120
?
A
解决问题
下一题
演示
如图,大风将一根木制旗杆吹裂,随时都可能倒下,十分危急。接警后“119”迅速赶到现场,并决定从断裂处将旗杆折断。现在需要划出一个安全警戒区域,那么你能确定这个安全区域的半径至少是多少米吗?
9m
24m
?
解决问题
下一题
拓展题:对比两个图形,你能直接观察验证出勾股定理吗?
两幅图中彩色的四个直角三角形总面积呢?
提示:图中的两个大正方形面积相等吗?
空白部分的面积呢?那剩余的
返回
课堂总结
①本节课学到了什么数学知识?
②你了解了勾股定理的发现方法了吗?
③你还有什么困惑?
返回
