人教版八年级数学下册课件-18.1.2 平行四边形的判定(17张)
文档属性
| 名称 | 人教版八年级数学下册课件-18.1.2 平行四边形的判定(17张) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-06 21:04:46 | ||
图片预览




文档简介
三角形的中位线定理
难点名称:三角形中位线定理证明及其应用
人教版八年级下册数学第18章
目录
CONTENTS
导入
知识讲解
学以致用
小结
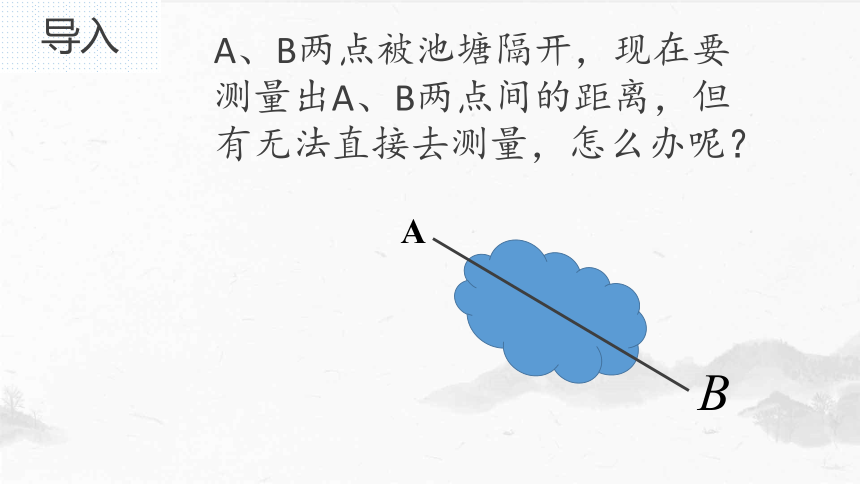
A、B两点被池塘隔开,现在要测量出A、B两点间的距离,但有无法直接去测量,怎么办呢?
导入
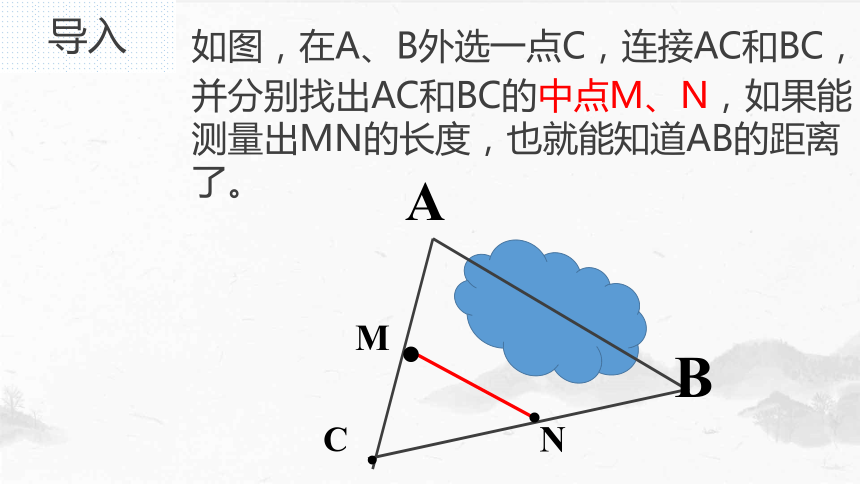
如图,在A、B外选一点C,连接AC和BC,
并分别找出AC和BC的中点M、N,如果能测量出MN的长度,也就能知道AB的距离了。
导入
C
B
A
E
D
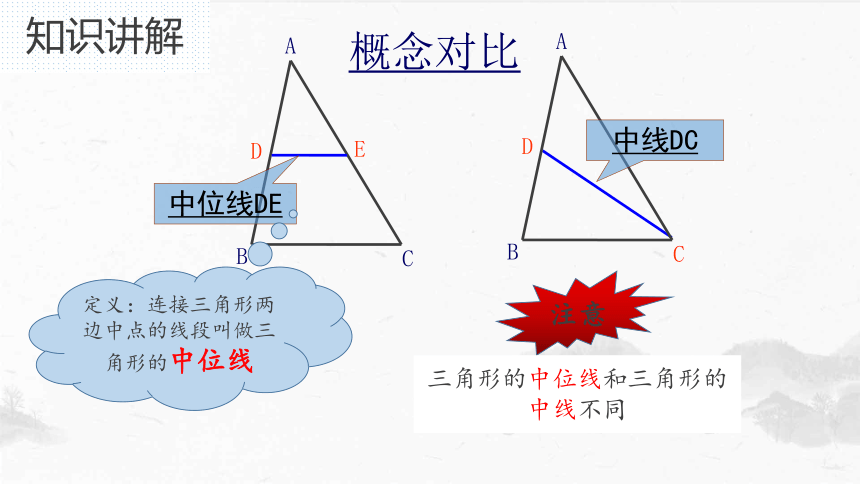
概念对比
C
B
A
D
中线DC
中位线DE
定义:连接三角形两边中点的线段叫做三角形的中位线
注意
三角形的中位线和三角形的中线不同
知识讲解
(1)相同之处——都和边的中点有关;
(2)不同之处:
三角形中位线是连接三角形两边的中点的线段;
三角形中线是连接一个顶点和它对边中点的线段
区分三角形的中位线和中线
三角形的中位线有三条
知识讲解
走进画板演示
A
B
C
D
E
合作探究
观察猜想
在△ABC中,中位线DE和边BC有怎样的位置关系和数量关系?
DE和边BC关系
位置关系:
数量关系:
DE∥BC
DE= BC
知识讲解
已知:如图:在△ABC中,D是AB的中点,E是AC的中点。
求证:
D
A
B
C
E
F
三角形的中位线平行于第三边,且等于第三边的一半
三角形中位线定理
三角形的中位线平行且等于第三边的一半。
几何语言:
∵DE是△ABC的中位线
C
E
D
B
A
①证明平行问题。
②证明一条线段是另一条线段的两倍或一半。
用途
1.已知:如图, E、F分别为AB、AC的中点。
(1)∵ E、F分别为AB、AC的中点。
∴ _____∥____ ,
______=_______ 或______= ______ ? ????
5
12
A
B
C
E
F
EF
EF
BC
BC
2EF
BC
学以致用
(2)若BC =10cm,则EF =____cm
(3)若EF =6cm, 则BC =__ __cm。
A.3cm B.6cm C.9cm D.12cm
B
学以致用
学以致用
3.已知: 如图,△ ABC 的各边分别为6cm,9cm, 10cm,则连结△ABC 各边中点所成的三角形的周长为_____cm。
12.5
如图,顺次连结四边形ABCD各边中点E,F,H,M,得到的四边形EFGH是平行四边形吗?为什么?
A
B
C
D
E
F
G
H
能力提升
∴EF∥HG,且EF=HG.
所以四边形EFGH是平行四边形.
解:连结AC.
∵EF是△ABC的一条中位线,
又∵HG是△DAC的一条中位线,
∴EF∥AC,且
∴HG∥AC,且
A
B
C
D
E
F
G
H
小结
三角形中位线定义:连接三角形两边中点的线段叫做三角形的中位线。
三角形中位线性质:三角形的中位线平行于第三边,且等于第三边的一半。
任意四边形四边中点连线所组成的四边形是:平行四边行
谢谢指导!
学 习 名 言
构成我们学习最大障碍的是已知的东西,而不是未知的东西。
—贝尔纳
难点名称:三角形中位线定理证明及其应用
人教版八年级下册数学第18章
目录
CONTENTS
导入
知识讲解
学以致用
小结
A、B两点被池塘隔开,现在要测量出A、B两点间的距离,但有无法直接去测量,怎么办呢?
导入
如图,在A、B外选一点C,连接AC和BC,
并分别找出AC和BC的中点M、N,如果能测量出MN的长度,也就能知道AB的距离了。
导入
C
B
A
E
D
概念对比
C
B
A
D
中线DC
中位线DE
定义:连接三角形两边中点的线段叫做三角形的中位线
注意
三角形的中位线和三角形的中线不同
知识讲解
(1)相同之处——都和边的中点有关;
(2)不同之处:
三角形中位线是连接三角形两边的中点的线段;
三角形中线是连接一个顶点和它对边中点的线段
区分三角形的中位线和中线
三角形的中位线有三条
知识讲解
走进画板演示
A
B
C
D
E
合作探究
观察猜想
在△ABC中,中位线DE和边BC有怎样的位置关系和数量关系?
DE和边BC关系
位置关系:
数量关系:
DE∥BC
DE= BC
知识讲解
已知:如图:在△ABC中,D是AB的中点,E是AC的中点。
求证:
D
A
B
C
E
F
三角形的中位线平行于第三边,且等于第三边的一半
三角形中位线定理
三角形的中位线平行且等于第三边的一半。
几何语言:
∵DE是△ABC的中位线
C
E
D
B
A
①证明平行问题。
②证明一条线段是另一条线段的两倍或一半。
用途
1.已知:如图, E、F分别为AB、AC的中点。
(1)∵ E、F分别为AB、AC的中点。
∴ _____∥____ ,
______=_______ 或______= ______ ? ????
5
12
A
B
C
E
F
EF
EF
BC
BC
2EF
BC
学以致用
(2)若BC =10cm,则EF =____cm
(3)若EF =6cm, 则BC =__ __cm。
A.3cm B.6cm C.9cm D.12cm
B
学以致用
学以致用
3.已知: 如图,△ ABC 的各边分别为6cm,9cm, 10cm,则连结△ABC 各边中点所成的三角形的周长为_____cm。
12.5
如图,顺次连结四边形ABCD各边中点E,F,H,M,得到的四边形EFGH是平行四边形吗?为什么?
A
B
C
D
E
F
G
H
能力提升
∴EF∥HG,且EF=HG.
所以四边形EFGH是平行四边形.
解:连结AC.
∵EF是△ABC的一条中位线,
又∵HG是△DAC的一条中位线,
∴EF∥AC,且
∴HG∥AC,且
A
B
C
D
E
F
G
H
小结
三角形中位线定义:连接三角形两边中点的线段叫做三角形的中位线。
三角形中位线性质:三角形的中位线平行于第三边,且等于第三边的一半。
任意四边形四边中点连线所组成的四边形是:平行四边行
谢谢指导!
学 习 名 言
构成我们学习最大障碍的是已知的东西,而不是未知的东西。
—贝尔纳
