2020-2021学年高一数学人教A版必修2第1章1.1 柱、锥、台、球的结构特征 课件(共36张PPT)
文档属性
| 名称 | 2020-2021学年高一数学人教A版必修2第1章1.1 柱、锥、台、球的结构特征 课件(共36张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-06 21:53:21 | ||
图片预览








文档简介
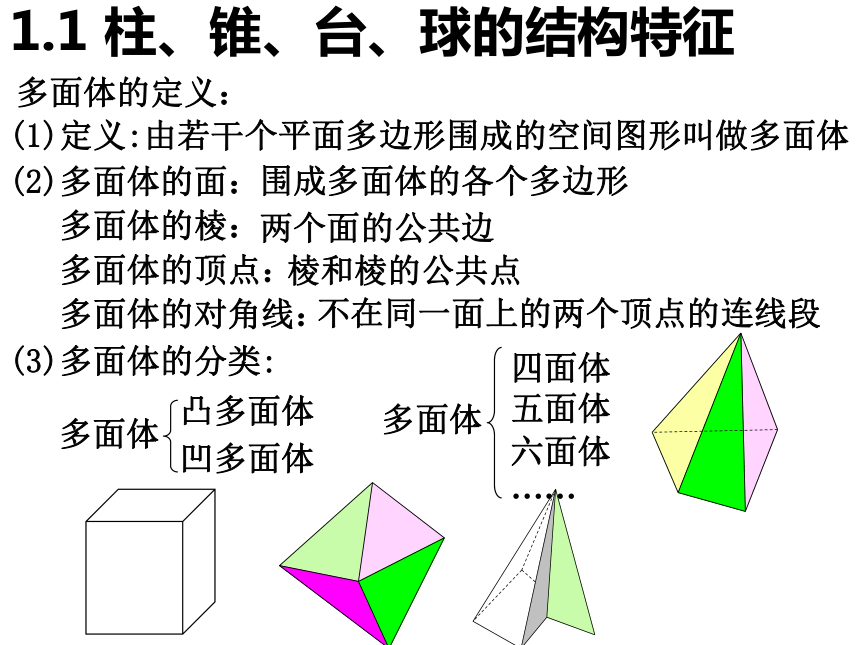
1.在初中,我们已经直观地认识了一些简单的几何体,如正方体、长方体、圆锥、圆柱、球等,仔细观察这些几何体的结构特征,通过总结,我们可以将正方体、长方体作为一类几何体,它们都是由平面多边形围成的几何体,称为多面体;圆锥、圆柱、球作为另一类几何体,它们是由平面图形旋转而成的几何体,称为旋转体.
2.我们看到的各种各样的建筑物,大都是由我们熟悉的几何体组成的.如国家游泳中心是2008年北京奥运会的标志性建筑之一,它的外观是长方体形状;国家奥林匹克主体育场“鸟巢”内部是半球形碗状坐席,如图.
[归纳总结] 对多面体概念的理解,注意以下几个方面:
(1)多面体是由平面多边形围成的,不是由圆面或其它曲面围成,也不是由空间多边形围成.
(2)本章所说的多边形,一般包括它内部的平面部分,故多面体是一个“封闭”的几何体.
(3)围成一个多面体至少要四个面.
(4)规定:在多面体中,不在同一面上的两个顶点的连线叫做多面体的对角线,不在同一面上的两条侧棱称为多面体的不相邻侧棱,侧棱和底面多边形的边统称为棱.
(5)一个多面体是由几个面围成,那么这个多面体称为几面体.
●知识衔接
我要问
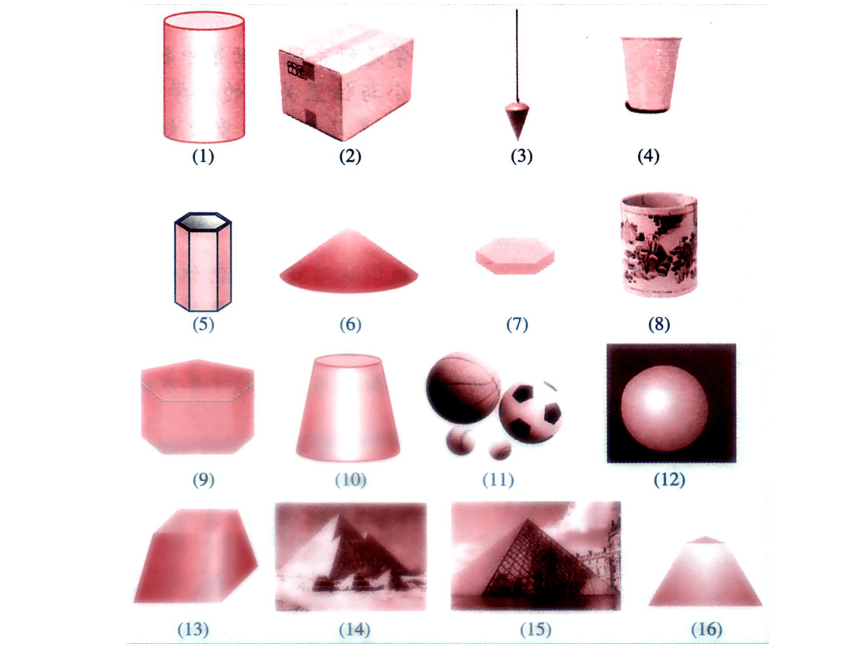
这些图片中的物体具有什么样的几何
结构特征?你能对它们进行分类吗?
我来答
上图中的物体大体可分为两大类.
其中(2),(5),(7),(9),(13),(14),(15),(16)
具有相同的特点:组成几何体的每个面都是平面图形,并且都是平面多边形;
(1),(3),(4),(6),(8),(10),(11),(12)
具有相同的特点:组成它们的面不全是平面图形.
想一想?
我们应该给上述两大类几何
体取个什么名字才好呢?
自主预习
我们把由一个平面图形绕它所在平面内的一条定____旋转所形成的____________叫做旋转体,这条定直线叫做旋转体的_______
旋转体
一般地,我们把由若干个____________围成的几何体叫做多面体,围成多面体的各个多边形叫做多面体的_____;相邻两个面的__________叫做多面体的棱;棱与棱的__________ 叫做多面体的顶点
多面体
在我们周围存在着各种各样的物体,它们都占据着空间的一部分.如果我们只考虑物体的_____和_____,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体
空间几
何体
定义
名称
形状
大小
平面多边形
面
公共边
公共点
直线
封闭几何体
轴
1.1 柱、锥、台、球的结构特征
多面体的定义:
(1)定义:由若干个平面多边形围成的空间图形叫做多面体
(2)多面体的面:
多面体的棱:
多面体的顶点:
多面体的对角线:
围成多面体的各个多边形
两个面的公共边
棱和棱的公共点
不在同一面上的两个顶点的连线段
(3)多面体的分类:
凸多面体
凹多面体
多面体
四面体
多面体
五面体
六面体
……
D
A
B
C
E
F
F’
A’
E’
D’
B’
C’
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
结构特征
有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行。
侧棱
侧面
底面
顶点
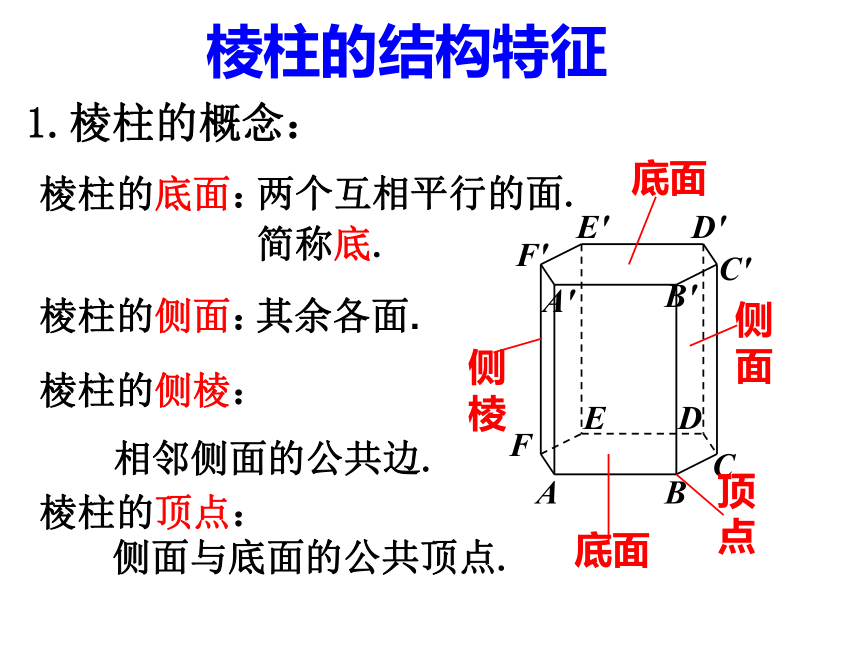
棱柱的结构特征
1.棱柱的概念:
A
B
C
D
E
F
A'
B'
C'
D'
E'
F'
棱柱的底面:
两个互相平行的面.
简称底.
底面
底面
棱柱的侧面:
其余各面.
棱柱的侧棱:
相邻侧面的公共边.
棱柱的顶点:
侧面与底面的公共顶点.
侧
面
侧
棱
顶
点
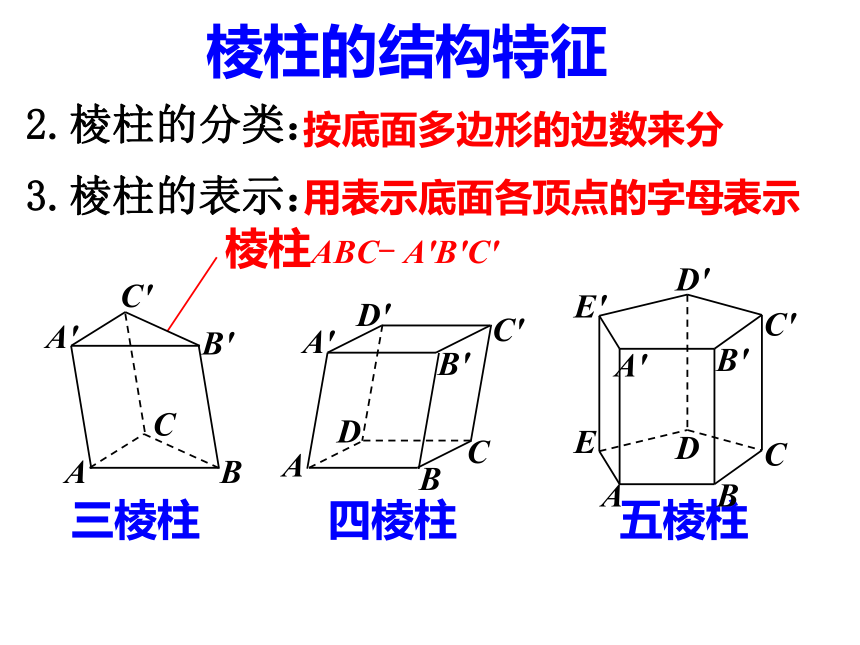
棱柱的结构特征
2.棱柱的分类:
按底面多边形的边数来分
三棱柱
四棱柱
五棱柱
3.棱柱的表示:
棱柱ABC- A'B'C'
用表示底面各顶点的字母表示
D'
A
B
C
D
E
A'
B'
C'
E'
A
B
C
D
A'
B'
C'
D'
A
B
C
A'
B'
C'
棱柱的结构特征
A
B
C
D
E
F
A'
B'
C'
D'
E'
F'
思考:对于棱柱,
1.侧棱长相等吗?
侧面是什么四边形?
平行四边形
相等
2.两个底面多边形是什么关系?
与平行于底面的截面呢?
全等
3.过不相邻的两条侧棱的截面是什么四边形?
平行四边形
棱柱的结构特征
4.棱柱的性质:
(1)侧棱相等,侧面都是平行四边形;
(2)两个底面与平行于底面的截面是全等多边形;
(3)过不相邻的两条侧棱的截面是平行四边形.
A
B
C
D
E
F
A'
B'
C'
D'
E'
F'
例2.有两个面互相平行,其余各面都是
平行四边形的几何体是不是棱柱?
长方体:
侧面和底面都是矩形的棱柱.
正方体:
侧面和底面都是正方形的棱柱.
典型例题
例1 下列几何体是棱柱的有( )
A.5个 B.4个 C.3个 D.2个
D
①过BC的截面截去长方体的一角,截去的几何体是不是棱柱,余下的几何体是不是棱柱?
棱柱定义的理解
②观察长方体,共有多少对平行平面?能作为棱柱的底面的有几对?
答:三对平行平面;这三对都可以作为棱柱的底面.
答:都是棱柱.
③观察右边的棱柱,共有多少对平行平面?能作为棱柱的底面的有几对?
答:四对平行平面;只有一对可以作为棱柱的底面.
棱柱定义的理解
④为什么定义中要说“其余各面都是四边形,并且相邻两个四边形的公共边都互相平行,”而不简单的只说“其余各面是平行四边形呢”?
答:满足“有两个面互相平行,其余各面都是平行四边形的几何体”这样说法的还有右图情况,如图所示.所以定义中不能简单描述成“其余各面都是平行四边形”.
棱柱定义的理解
巩固提高
1.下列说法正确的是( )
A棱柱的面中,至少有两个面互相平行
B棱柱中两个互相平行的面一定是棱柱的底面
C棱柱中一条侧棱就是棱柱的高
D棱柱的侧面一定是平行四边形,但它的底面一定不是平行四边形
A
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
S
A
B
C
D
顶点
侧面
侧棱
底面
结构特征
有一个面是多边形,其余各面都是有一个公共顶点的三角形。
棱锥的结构特征
1.棱锥的概念:
一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥.
棱锥的结构特征
1.棱锥的概念:
棱锥的底面:
多边形面.
简称底.
底面
顶点
棱锥的侧面:
有公共顶点的
各个三角形面.
棱锥的侧棱:
相邻侧面的公共边.
棱锥的顶点:
各侧面的公共顶点.
侧
棱
侧
面
棱锥的结构特征
2.棱锥的分类:
按底面多边形的边数来分
三棱锥
四棱锥
五棱锥
3.棱锥的表示:
棱锥S-ABC
用顶点各底面各顶点的字母表示
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
结构特征
A
B
C
D
A’
B’
C’
D’
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分是棱台.
棱台的结构特征
1.棱台的概念:
棱台的底面:
原棱锥的底面和截面分别叫做棱台的下底面和上底面。
下底面
侧
棱
顶
点
侧
面
上底面
棱台的结构特征
1.棱台的概念:
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台.
2.棱台的分类:
由三棱锥、四棱锥、五棱锥……截得的棱台分别叫做三棱台、四棱台、五棱台……
三棱台
四棱台
五棱台
3.棱台的表示:
棱台ABCD-A‘B’C‘D’
用顶点各底面各顶点的字母表示
B’
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
A
A’
O
B
O’
轴
底面
侧面
母线
结构特征
以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱。
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
S
顶点
A
B
O
底面
轴
侧面
母线
结构特征
以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫做圆锥。
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
结构特征
O
O’
用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分是圆台.
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
结构特征
O
半径
球心
以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体.
球的结构特征
球:以半圆的直径所在的直线为旋转轴,半圆面旋转一周形成的几何体叫做球体。
直径
O
A
B
C
球心
大圆
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
(1)棱柱与圆柱统称为柱体。
(2)棱锥与圆锥统称为锥体。
旋转体
(2)棱台与圆台统称为台体。
多面体
巩固提高
2.如图,观察四个几何体,其中判断正确的是( )
A.(1)是棱台 B.(2)是圆台
C.(3)是棱锥 D.(4)不是棱柱
C
巩固提高
3.有下列四种说法:
①圆柱是将矩形旋转一周所得的几何体;
②以直角三角形的一直角边为旋转轴,旋转所得的几何体是圆锥;
③圆台的任意两条母线的延长线,可能相交也可能不相交;
④圆锥的底面是圆面,侧面是曲面;
其中错误的有( )
A 1个 B 2个 C 3个 D 4个
C
巩固提高
4.下列说法
①圆柱的轴截面是过母线的截面中最大的一个;
②用任意一个平面去截球体得到的截面一定是一个圆面;
③用任意一个平面去截圆锥得到的截面一定是一个圆;
其中正确的个数是( )
A 0个 B 1个 C 2个 D 3个
C
巩固提高
5.设圆锥的母线长为,高为,过圆锥的两条母线作一个截面,则截面面积的最大值为
____________________。
巩固提高
6.以直角边为3 cm和4 cm的直角三角形绕其直角边旋转而形成的圆锥,母线长为
______________.
5 cm
典型例题
例2,圆台的一个底面周长是另一个底面周长的3倍,轴截面的面积等于 ,母线与轴的夹角是45°,求这个圆台的高、母线长和底面半径。
典型例题
解:圆台的轴截面如图所示:
设圆台上、下底面半径分别为x cm和3x cm,延长 交 的延长线于S.在Rt△SOA中,∠ASO=45°,则∠SAO=45°.所SO=AO=3x.所以 =2x.又(6x+2x)·x=392,解得x=7,所以圆台的高 =14 cm,母线长l= cm,而底面半径分别为7 cm和21 cm,
即圆台的高14 cm,母线长 cm,底面半径分别为7 cm和21 cm.
巩固提高
1.下列命题中正确的是
A.有两个面平行,其余各面都是四边形的几何体叫棱柱
B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱
C.有一个面是多边形,其余各面都是三角形的几何体叫棱锥
D.棱台各侧棱的延长线交于一点
D
巩固提高
2.下列命题中正确的是
A.以直角三角形的一直角边为轴旋转所得的旋转体是圆锥
B.以直角梯形的一腰为轴旋转所得的旋转体是圆台
C.圆柱、圆锥、圆台都有两个底面
D.圆锥的侧面展开图为扇形,这个扇形所在圆的半径等于圆锥底面圆的半径
A
巩固提高
3.下面几何体中,过轴的截面一定是圆面的是
A.圆柱 B.圆锥
C.球 D.圆台
C
巩固提高
4.一个无盖的正方体盒子展开后的平面图,如图所示,A、B、C是展开图上的三点,则在正方体盒子中∠ABC=____________.
巩固提高
解:如下图所示,折成正方体,很明显点A、B、C是上底面正方形的三个顶点,
则∠ABC=90°。
锥
体
柱
体
台
体
柱、锥、台体的关系
棱柱、棱锥、棱台之间有什么关系?圆柱、圆锥、圆台之间呢?柱、锥、台体之间有什么关系?
上底扩大
上底缩小
上底缩小
上底扩大
几何体的分类
柱体
锥体
台体
球
多面体
旋转体
练习:
1、下列命题是真命题的是( )
A 以直角三角形的一直角边所在的直线为轴旋转所得的几何体为圆锥;
B 以直角梯形的一腰所在的直线为轴旋转所得的旋转体为圆柱;
C 圆柱、圆锥、棱锥的底面都是圆;
D 有一个面为多边形,其他各面都是三角形的几何体是棱锥。
A
2、过球面上的两点作球的大圆,可以作( )个。
1或无数多
3.下图中不可能围成正方体的是( )
A
D
C
B
B
4.在棱柱中………………..( )
A . 只有两个面平行
B . 所有的棱都相等
C . 所有的面都是平行四边形
D . 两底面平行,并且各侧棱也平行
D
知识小结
简单几何体的结构特征
柱体
锥体
台体
球
棱柱
圆柱
棱锥
圆锥
棱台
圆台
2.我们看到的各种各样的建筑物,大都是由我们熟悉的几何体组成的.如国家游泳中心是2008年北京奥运会的标志性建筑之一,它的外观是长方体形状;国家奥林匹克主体育场“鸟巢”内部是半球形碗状坐席,如图.
[归纳总结] 对多面体概念的理解,注意以下几个方面:
(1)多面体是由平面多边形围成的,不是由圆面或其它曲面围成,也不是由空间多边形围成.
(2)本章所说的多边形,一般包括它内部的平面部分,故多面体是一个“封闭”的几何体.
(3)围成一个多面体至少要四个面.
(4)规定:在多面体中,不在同一面上的两个顶点的连线叫做多面体的对角线,不在同一面上的两条侧棱称为多面体的不相邻侧棱,侧棱和底面多边形的边统称为棱.
(5)一个多面体是由几个面围成,那么这个多面体称为几面体.
●知识衔接
我要问
这些图片中的物体具有什么样的几何
结构特征?你能对它们进行分类吗?
我来答
上图中的物体大体可分为两大类.
其中(2),(5),(7),(9),(13),(14),(15),(16)
具有相同的特点:组成几何体的每个面都是平面图形,并且都是平面多边形;
(1),(3),(4),(6),(8),(10),(11),(12)
具有相同的特点:组成它们的面不全是平面图形.
想一想?
我们应该给上述两大类几何
体取个什么名字才好呢?
自主预习
我们把由一个平面图形绕它所在平面内的一条定____旋转所形成的____________叫做旋转体,这条定直线叫做旋转体的_______
旋转体
一般地,我们把由若干个____________围成的几何体叫做多面体,围成多面体的各个多边形叫做多面体的_____;相邻两个面的__________叫做多面体的棱;棱与棱的__________ 叫做多面体的顶点
多面体
在我们周围存在着各种各样的物体,它们都占据着空间的一部分.如果我们只考虑物体的_____和_____,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体
空间几
何体
定义
名称
形状
大小
平面多边形
面
公共边
公共点
直线
封闭几何体
轴
1.1 柱、锥、台、球的结构特征
多面体的定义:
(1)定义:由若干个平面多边形围成的空间图形叫做多面体
(2)多面体的面:
多面体的棱:
多面体的顶点:
多面体的对角线:
围成多面体的各个多边形
两个面的公共边
棱和棱的公共点
不在同一面上的两个顶点的连线段
(3)多面体的分类:
凸多面体
凹多面体
多面体
四面体
多面体
五面体
六面体
……
D
A
B
C
E
F
F’
A’
E’
D’
B’
C’
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
结构特征
有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行。
侧棱
侧面
底面
顶点
棱柱的结构特征
1.棱柱的概念:
A
B
C
D
E
F
A'
B'
C'
D'
E'
F'
棱柱的底面:
两个互相平行的面.
简称底.
底面
底面
棱柱的侧面:
其余各面.
棱柱的侧棱:
相邻侧面的公共边.
棱柱的顶点:
侧面与底面的公共顶点.
侧
面
侧
棱
顶
点
棱柱的结构特征
2.棱柱的分类:
按底面多边形的边数来分
三棱柱
四棱柱
五棱柱
3.棱柱的表示:
棱柱ABC- A'B'C'
用表示底面各顶点的字母表示
D'
A
B
C
D
E
A'
B'
C'
E'
A
B
C
D
A'
B'
C'
D'
A
B
C
A'
B'
C'
棱柱的结构特征
A
B
C
D
E
F
A'
B'
C'
D'
E'
F'
思考:对于棱柱,
1.侧棱长相等吗?
侧面是什么四边形?
平行四边形
相等
2.两个底面多边形是什么关系?
与平行于底面的截面呢?
全等
3.过不相邻的两条侧棱的截面是什么四边形?
平行四边形
棱柱的结构特征
4.棱柱的性质:
(1)侧棱相等,侧面都是平行四边形;
(2)两个底面与平行于底面的截面是全等多边形;
(3)过不相邻的两条侧棱的截面是平行四边形.
A
B
C
D
E
F
A'
B'
C'
D'
E'
F'
例2.有两个面互相平行,其余各面都是
平行四边形的几何体是不是棱柱?
长方体:
侧面和底面都是矩形的棱柱.
正方体:
侧面和底面都是正方形的棱柱.
典型例题
例1 下列几何体是棱柱的有( )
A.5个 B.4个 C.3个 D.2个
D
①过BC的截面截去长方体的一角,截去的几何体是不是棱柱,余下的几何体是不是棱柱?
棱柱定义的理解
②观察长方体,共有多少对平行平面?能作为棱柱的底面的有几对?
答:三对平行平面;这三对都可以作为棱柱的底面.
答:都是棱柱.
③观察右边的棱柱,共有多少对平行平面?能作为棱柱的底面的有几对?
答:四对平行平面;只有一对可以作为棱柱的底面.
棱柱定义的理解
④为什么定义中要说“其余各面都是四边形,并且相邻两个四边形的公共边都互相平行,”而不简单的只说“其余各面是平行四边形呢”?
答:满足“有两个面互相平行,其余各面都是平行四边形的几何体”这样说法的还有右图情况,如图所示.所以定义中不能简单描述成“其余各面都是平行四边形”.
棱柱定义的理解
巩固提高
1.下列说法正确的是( )
A棱柱的面中,至少有两个面互相平行
B棱柱中两个互相平行的面一定是棱柱的底面
C棱柱中一条侧棱就是棱柱的高
D棱柱的侧面一定是平行四边形,但它的底面一定不是平行四边形
A
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
S
A
B
C
D
顶点
侧面
侧棱
底面
结构特征
有一个面是多边形,其余各面都是有一个公共顶点的三角形。
棱锥的结构特征
1.棱锥的概念:
一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥.
棱锥的结构特征
1.棱锥的概念:
棱锥的底面:
多边形面.
简称底.
底面
顶点
棱锥的侧面:
有公共顶点的
各个三角形面.
棱锥的侧棱:
相邻侧面的公共边.
棱锥的顶点:
各侧面的公共顶点.
侧
棱
侧
面
棱锥的结构特征
2.棱锥的分类:
按底面多边形的边数来分
三棱锥
四棱锥
五棱锥
3.棱锥的表示:
棱锥S-ABC
用顶点各底面各顶点的字母表示
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
结构特征
A
B
C
D
A’
B’
C’
D’
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分是棱台.
棱台的结构特征
1.棱台的概念:
棱台的底面:
原棱锥的底面和截面分别叫做棱台的下底面和上底面。
下底面
侧
棱
顶
点
侧
面
上底面
棱台的结构特征
1.棱台的概念:
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台.
2.棱台的分类:
由三棱锥、四棱锥、五棱锥……截得的棱台分别叫做三棱台、四棱台、五棱台……
三棱台
四棱台
五棱台
3.棱台的表示:
棱台ABCD-A‘B’C‘D’
用顶点各底面各顶点的字母表示
B’
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
A
A’
O
B
O’
轴
底面
侧面
母线
结构特征
以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱。
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
S
顶点
A
B
O
底面
轴
侧面
母线
结构特征
以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫做圆锥。
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
结构特征
O
O’
用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分是圆台.
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
结构特征
O
半径
球心
以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体.
球的结构特征
球:以半圆的直径所在的直线为旋转轴,半圆面旋转一周形成的几何体叫做球体。
直径
O
A
B
C
球心
大圆
棱柱
棱锥
圆柱
圆锥
圆台
棱台
球
(1)棱柱与圆柱统称为柱体。
(2)棱锥与圆锥统称为锥体。
旋转体
(2)棱台与圆台统称为台体。
多面体
巩固提高
2.如图,观察四个几何体,其中判断正确的是( )
A.(1)是棱台 B.(2)是圆台
C.(3)是棱锥 D.(4)不是棱柱
C
巩固提高
3.有下列四种说法:
①圆柱是将矩形旋转一周所得的几何体;
②以直角三角形的一直角边为旋转轴,旋转所得的几何体是圆锥;
③圆台的任意两条母线的延长线,可能相交也可能不相交;
④圆锥的底面是圆面,侧面是曲面;
其中错误的有( )
A 1个 B 2个 C 3个 D 4个
C
巩固提高
4.下列说法
①圆柱的轴截面是过母线的截面中最大的一个;
②用任意一个平面去截球体得到的截面一定是一个圆面;
③用任意一个平面去截圆锥得到的截面一定是一个圆;
其中正确的个数是( )
A 0个 B 1个 C 2个 D 3个
C
巩固提高
5.设圆锥的母线长为,高为,过圆锥的两条母线作一个截面,则截面面积的最大值为
____________________。
巩固提高
6.以直角边为3 cm和4 cm的直角三角形绕其直角边旋转而形成的圆锥,母线长为
______________.
5 cm
典型例题
例2,圆台的一个底面周长是另一个底面周长的3倍,轴截面的面积等于 ,母线与轴的夹角是45°,求这个圆台的高、母线长和底面半径。
典型例题
解:圆台的轴截面如图所示:
设圆台上、下底面半径分别为x cm和3x cm,延长 交 的延长线于S.在Rt△SOA中,∠ASO=45°,则∠SAO=45°.所SO=AO=3x.所以 =2x.又(6x+2x)·x=392,解得x=7,所以圆台的高 =14 cm,母线长l= cm,而底面半径分别为7 cm和21 cm,
即圆台的高14 cm,母线长 cm,底面半径分别为7 cm和21 cm.
巩固提高
1.下列命题中正确的是
A.有两个面平行,其余各面都是四边形的几何体叫棱柱
B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱
C.有一个面是多边形,其余各面都是三角形的几何体叫棱锥
D.棱台各侧棱的延长线交于一点
D
巩固提高
2.下列命题中正确的是
A.以直角三角形的一直角边为轴旋转所得的旋转体是圆锥
B.以直角梯形的一腰为轴旋转所得的旋转体是圆台
C.圆柱、圆锥、圆台都有两个底面
D.圆锥的侧面展开图为扇形,这个扇形所在圆的半径等于圆锥底面圆的半径
A
巩固提高
3.下面几何体中,过轴的截面一定是圆面的是
A.圆柱 B.圆锥
C.球 D.圆台
C
巩固提高
4.一个无盖的正方体盒子展开后的平面图,如图所示,A、B、C是展开图上的三点,则在正方体盒子中∠ABC=____________.
巩固提高
解:如下图所示,折成正方体,很明显点A、B、C是上底面正方形的三个顶点,
则∠ABC=90°。
锥
体
柱
体
台
体
柱、锥、台体的关系
棱柱、棱锥、棱台之间有什么关系?圆柱、圆锥、圆台之间呢?柱、锥、台体之间有什么关系?
上底扩大
上底缩小
上底缩小
上底扩大
几何体的分类
柱体
锥体
台体
球
多面体
旋转体
练习:
1、下列命题是真命题的是( )
A 以直角三角形的一直角边所在的直线为轴旋转所得的几何体为圆锥;
B 以直角梯形的一腰所在的直线为轴旋转所得的旋转体为圆柱;
C 圆柱、圆锥、棱锥的底面都是圆;
D 有一个面为多边形,其他各面都是三角形的几何体是棱锥。
A
2、过球面上的两点作球的大圆,可以作( )个。
1或无数多
3.下图中不可能围成正方体的是( )
A
D
C
B
B
4.在棱柱中………………..( )
A . 只有两个面平行
B . 所有的棱都相等
C . 所有的面都是平行四边形
D . 两底面平行,并且各侧棱也平行
D
知识小结
简单几何体的结构特征
柱体
锥体
台体
球
棱柱
圆柱
棱锥
圆锥
棱台
圆台
