1.1.1 棱柱、棱锥、棱台的结构特征(课件)-2020-2021学年高一数学精品备课课件资源(人教A版必修2)(28张PPT)
文档属性
| 名称 | 1.1.1 棱柱、棱锥、棱台的结构特征(课件)-2020-2021学年高一数学精品备课课件资源(人教A版必修2)(28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-09 13:28:47 | ||
图片预览



文档简介
§1.1.1
棱柱、棱锥、棱台的结构特征
人教A版数学必修2第一章《空间几何体》
【学习目标】
1.通过观察实例,认识棱柱、棱锥、棱台的结构特征.
2.理解棱柱、棱锥、棱台之间的关系.
3.能运用棱柱、棱锥、棱台的结构特征描述现实生活中简单物体的结构.
形状
大小
空间图形
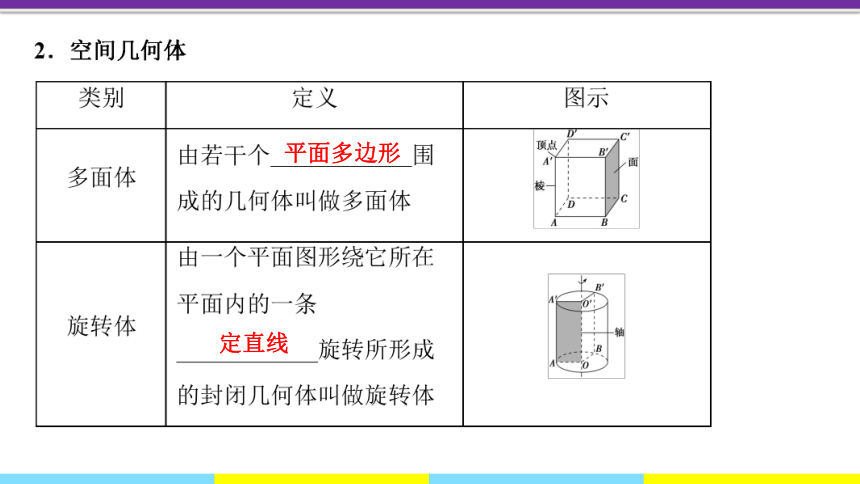
自主预面多边形
定直线
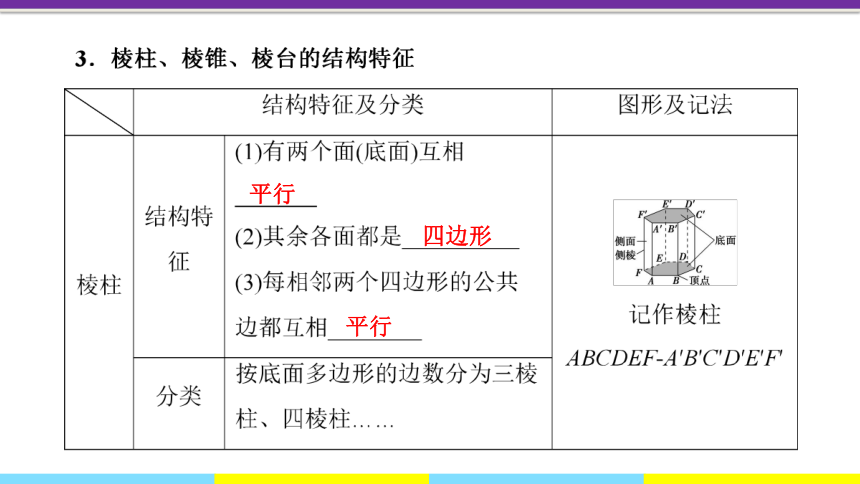
平行
四边形
平行
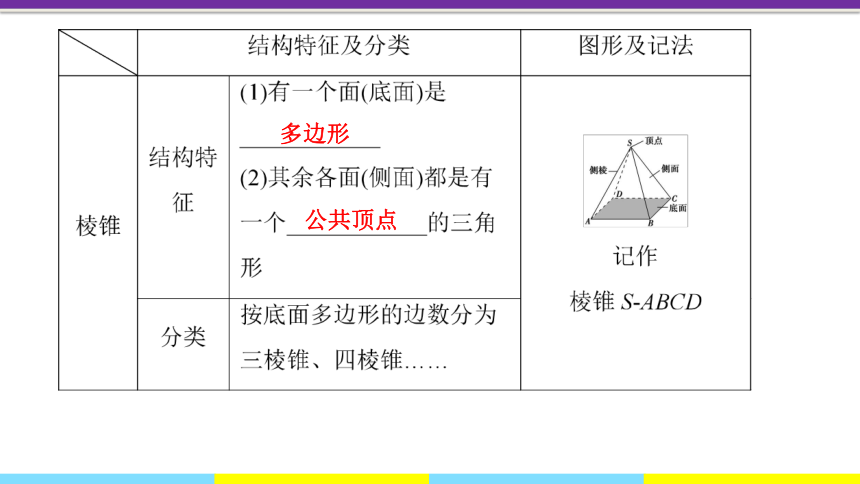
多边形
公共顶点
知识点一
棱柱、棱锥、棱台的结构特征
2
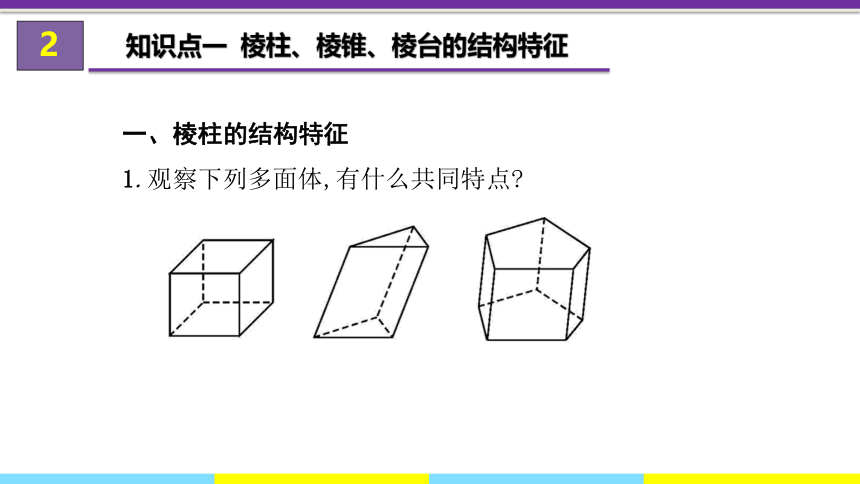
一、棱柱的结构特征
1.观察下列多面体,有什么共同特点?
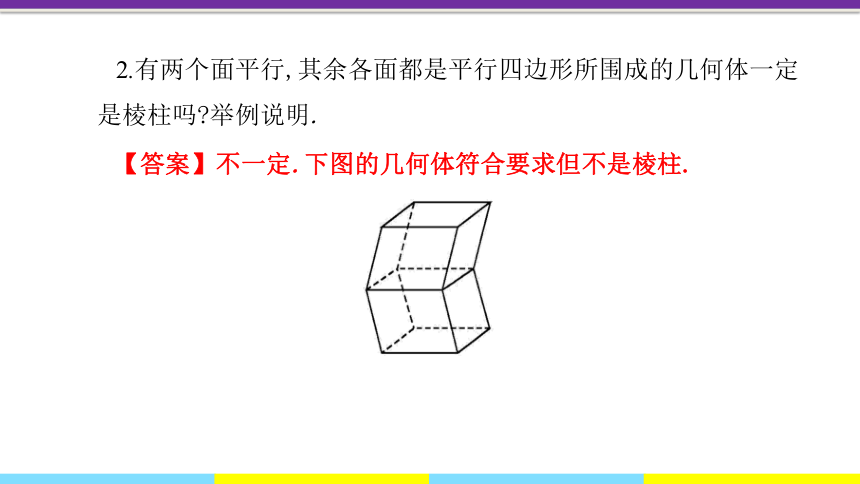
2.有两个面平行,其余各面都是平行四边形所围成的几何体一定是棱柱吗?举例说明.
【答案】不一定.下图的几何体符合要求但不是棱柱.
3.关于棱柱的定义、分类、图示及其表示
定义:有两个面
,其余各面都是
,并且每相邻两个四边形的公共边都
,由这些面所围成的多面体叫做棱柱.
相关概念:底面(底):两个互相
的面;侧面:
;
侧棱:相邻侧面的
;顶点:
的公共顶点
分类:①依据:底面多边形的
;
②举例:
(底面是三角形)、
(底面是四边形)……
图形及表示:
如图棱柱可记作:棱柱ABCDEF-A'B'C'D'E'F'
互相平行
互相平行
四边形
平行
其余各面
公共边
侧面和底面
边数
三棱柱
四棱柱
二、棱锥的结构特征
1.观察下列多面体,有什么共同特点?
【回答】(1)有一个面是多边形;(2)其余各面都是有一个公共顶点的三角形.
2.关于棱锥的定义、分类、图形及表示
定义:有一个面是
,其余各面都是
的三角形,由这些面所围成的多面体叫做棱锥
相关概念:底面(底):
面;侧面:有
的各个三角形面;侧棱:相邻侧面的
;顶点:各侧面的公共顶点
分类:①依据:底面多边形的边数;②举例:
(底面是三角形)、四棱锥(底面是四边形)……
如图棱锥可记作:棱锥S-ABCD
图形及表示:
多边形
有一个公共定点
多边形
公共顶点
公共边
三棱锥
三、棱台的结构特征
1.观察下列多面体,分析其与棱锥有何区别与联系?
【答案】(1)区别:该几何体有两个面相互平行而棱锥没有.
(2)联系:用平行于棱锥底面的平面去截棱锥,其底面和截面之间的
部分即为该几何体.
2.观察下面的几何体是否为棱台?为什么?
【答案】不是.因为延长各侧棱不能还原成棱锥.
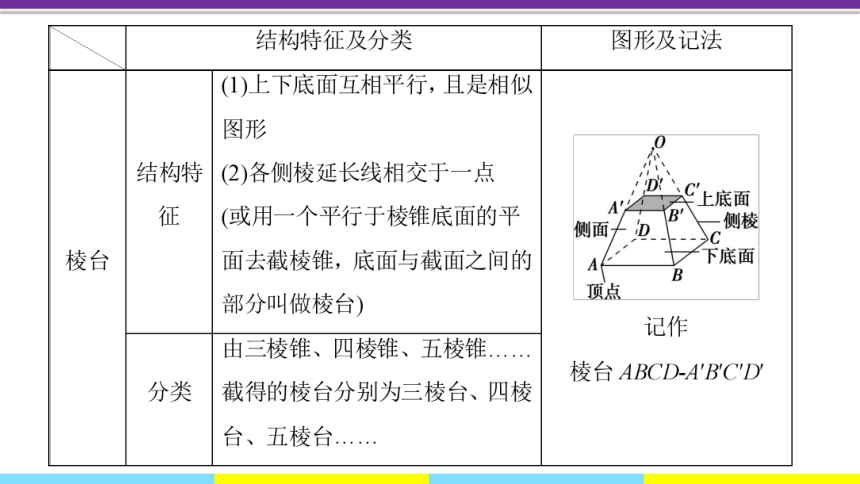
3.关于棱台的定义、分类、图形及表示
定义:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台
相关概念:上底面:原棱锥的截面;下底面:原棱锥的底面;侧面:其余各面;侧棱:相邻侧面的公共边;顶点:侧面与上(下)底面的公共顶点.
分类:①依据:由几棱锥截得;
②举例:三棱台(由三棱锥截得)、_______(由四棱锥截得)……
图形及表示:
如图棱台可记作:棱台ABCD-A'B'C'D'
四棱台
【例题1】下面的几何体中是棱柱的有( )
A
.
3个
B
.4个
C
.5个
D.6个
【解析】棱柱有三个特征:(1)有两个面相互平行;(2)其余各面是四边形;(3)侧棱相互平行.本题所给几何体中⑥⑦不符合棱柱的三个特征,而①②③④⑤符合,故选C.
【答案】C
【例题2】下面图形中,为棱锥的是( )
A.①③
B.①③④
C.①②④
D.①②
【解析】根据棱锥的定义和结构特征可以判断,①②是棱锥,③不是棱锥,④是棱锥.故选C.
【答案】C
【例题3】下列图形中,是棱台的是( )
【解析】由棱台的定义知,A、D的侧棱延长线不交于一点,所以不是棱台;B中两个面不平行,不是棱台,只有C符合棱台的定义,故选C.
【答案】C
【例题4】下列几个命题:
①棱柱的底面一定是平行四边形;
②棱锥的底面一定是三角形;
③棱柱被平面分成的两部分可以都是棱柱.
其中正确的是________.(填序号)
【解析】①棱柱的底面可以为任意多边形.②棱锥的底面可以为四边形、五边形等.
【答案】③
【例6】长方体ABCD-A1B1C1D1中,AB=4,BC=3,BB1=5,一只蚂蚁从点A出发沿表面爬行到点C1,求蚂蚁爬行的最短路线.
1.棱柱、棱锥定义的关注点
(1)棱柱的定义有以下两个要点,缺一不可:
①有两个平面(底面)互相平行;
②其余各面(侧面)每相邻两个面的公共边(侧棱)都互相平行.
(2)棱锥的定义有以下两个要点,缺一不可:
①有一个面(底面)是多边形;
②其余各面(侧面)是有一个公共顶点的三角形.
2.根据几何体的结构特点判定几何体的类型,首先要熟练掌握各几何体的概念,把握好各类几何体的性质,其次要有一定的空间想象能力.
课堂小结
棱柱、棱锥、棱台的结构特征
人教A版数学必修2第一章《空间几何体》
【学习目标】
1.通过观察实例,认识棱柱、棱锥、棱台的结构特征.
2.理解棱柱、棱锥、棱台之间的关系.
3.能运用棱柱、棱锥、棱台的结构特征描述现实生活中简单物体的结构.
形状
大小
空间图形
自主预面多边形
定直线
平行
四边形
平行
多边形
公共顶点
知识点一
棱柱、棱锥、棱台的结构特征
2
一、棱柱的结构特征
1.观察下列多面体,有什么共同特点?
2.有两个面平行,其余各面都是平行四边形所围成的几何体一定是棱柱吗?举例说明.
【答案】不一定.下图的几何体符合要求但不是棱柱.
3.关于棱柱的定义、分类、图示及其表示
定义:有两个面
,其余各面都是
,并且每相邻两个四边形的公共边都
,由这些面所围成的多面体叫做棱柱.
相关概念:底面(底):两个互相
的面;侧面:
;
侧棱:相邻侧面的
;顶点:
的公共顶点
分类:①依据:底面多边形的
;
②举例:
(底面是三角形)、
(底面是四边形)……
图形及表示:
如图棱柱可记作:棱柱ABCDEF-A'B'C'D'E'F'
互相平行
互相平行
四边形
平行
其余各面
公共边
侧面和底面
边数
三棱柱
四棱柱
二、棱锥的结构特征
1.观察下列多面体,有什么共同特点?
【回答】(1)有一个面是多边形;(2)其余各面都是有一个公共顶点的三角形.
2.关于棱锥的定义、分类、图形及表示
定义:有一个面是
,其余各面都是
的三角形,由这些面所围成的多面体叫做棱锥
相关概念:底面(底):
面;侧面:有
的各个三角形面;侧棱:相邻侧面的
;顶点:各侧面的公共顶点
分类:①依据:底面多边形的边数;②举例:
(底面是三角形)、四棱锥(底面是四边形)……
如图棱锥可记作:棱锥S-ABCD
图形及表示:
多边形
有一个公共定点
多边形
公共顶点
公共边
三棱锥
三、棱台的结构特征
1.观察下列多面体,分析其与棱锥有何区别与联系?
【答案】(1)区别:该几何体有两个面相互平行而棱锥没有.
(2)联系:用平行于棱锥底面的平面去截棱锥,其底面和截面之间的
部分即为该几何体.
2.观察下面的几何体是否为棱台?为什么?
【答案】不是.因为延长各侧棱不能还原成棱锥.
3.关于棱台的定义、分类、图形及表示
定义:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台
相关概念:上底面:原棱锥的截面;下底面:原棱锥的底面;侧面:其余各面;侧棱:相邻侧面的公共边;顶点:侧面与上(下)底面的公共顶点.
分类:①依据:由几棱锥截得;
②举例:三棱台(由三棱锥截得)、_______(由四棱锥截得)……
图形及表示:
如图棱台可记作:棱台ABCD-A'B'C'D'
四棱台
【例题1】下面的几何体中是棱柱的有( )
A
.
3个
B
.4个
C
.5个
D.6个
【解析】棱柱有三个特征:(1)有两个面相互平行;(2)其余各面是四边形;(3)侧棱相互平行.本题所给几何体中⑥⑦不符合棱柱的三个特征,而①②③④⑤符合,故选C.
【答案】C
【例题2】下面图形中,为棱锥的是( )
A.①③
B.①③④
C.①②④
D.①②
【解析】根据棱锥的定义和结构特征可以判断,①②是棱锥,③不是棱锥,④是棱锥.故选C.
【答案】C
【例题3】下列图形中,是棱台的是( )
【解析】由棱台的定义知,A、D的侧棱延长线不交于一点,所以不是棱台;B中两个面不平行,不是棱台,只有C符合棱台的定义,故选C.
【答案】C
【例题4】下列几个命题:
①棱柱的底面一定是平行四边形;
②棱锥的底面一定是三角形;
③棱柱被平面分成的两部分可以都是棱柱.
其中正确的是________.(填序号)
【解析】①棱柱的底面可以为任意多边形.②棱锥的底面可以为四边形、五边形等.
【答案】③
【例6】长方体ABCD-A1B1C1D1中,AB=4,BC=3,BB1=5,一只蚂蚁从点A出发沿表面爬行到点C1,求蚂蚁爬行的最短路线.
1.棱柱、棱锥定义的关注点
(1)棱柱的定义有以下两个要点,缺一不可:
①有两个平面(底面)互相平行;
②其余各面(侧面)每相邻两个面的公共边(侧棱)都互相平行.
(2)棱锥的定义有以下两个要点,缺一不可:
①有一个面(底面)是多边形;
②其余各面(侧面)是有一个公共顶点的三角形.
2.根据几何体的结构特点判定几何体的类型,首先要熟练掌握各几何体的概念,把握好各类几何体的性质,其次要有一定的空间想象能力.
课堂小结
