1.4.2 角平分线的性质与判定 课件(共19张PPT)
文档属性
| 名称 | 1.4.2 角平分线的性质与判定 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-06 18:29:09 | ||
图片预览






文档简介
第4节 角平分线的性质与判定
(第2课时)
第一章 三角形的证明
2020-2021北师大版八年级数学下册
1 证明三角形的三条角平分线交于一点.
2 应用角平分线定理解决数学问题.
学习目标
角平分线的性质与判定的内容是什么?
定理 角平分线上的点到这个角的两边的距离相等.
定理 在一个角的内部,到角的两边距离相等的点在这个角的 平分线上.
新课导入
角平分线的性质
知识点一
作三角形的三个内角的角平分线,你发现了什么?
发现:三角形的三个内角的角平分线交于一点,并且这一点到三角形三边的距离相等.
探究新知
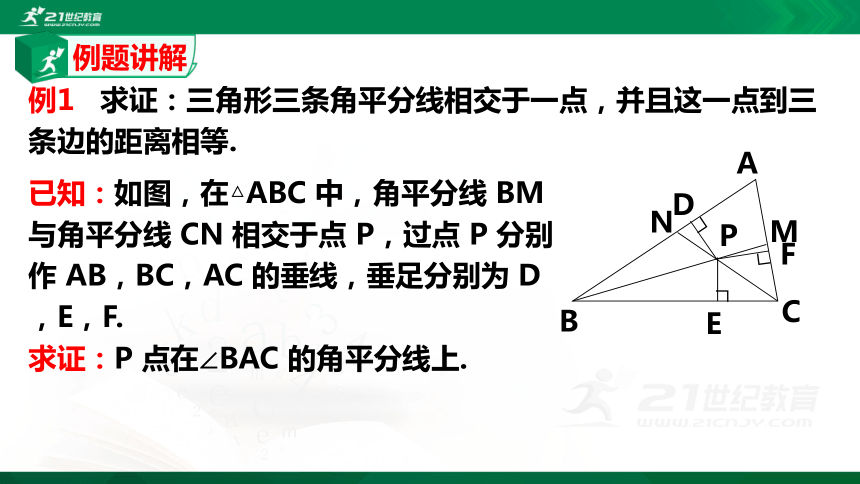
例1 求证:三角形三条角平分线相交于一点,并且这一点到三条边的距离相等.
已知:如图,在△ABC 中,角平分线 BM 与角平分线 CN 相交于点 P,过点 P 分别作 AB,BC,AC 的垂线,垂足分别为 D,E,F.
求证:P 点在∠BAC 的角平分线上.
A
B
C
P
E
F
M
D
N
例题讲解
证明∵BM是△ABC的角平分线,点P在BM上,且
PD丄AB,PE丄BC,垂足分别为D,E,
∴PD=PE (角平分线上的点到这个角的两边的距离相等).
同理,PE=PF.
∴PD=PE=PF.
∴点P在∠A的平分线上(在一个角的内部,到角的两边距离相等的点在这个角的平分线上),
即∠A的平分线经过点P.
三角形的三条角平分线相交于一点,并且这一点到三角形三条边的距离相等.
三边垂直平分线
三条角平分线
三角形
锐角三角形
交于三角形内一点
交于三角形内一点
钝角三角形
交于三角形外一点
直角三角形
交于斜边的中点
交点性质
到三角形三个顶点的距离相等
到三角形三边的距离相等
例2 如图,在△ABC中,∠ABC与∠ACB的平分线相交于点O,过点O作DE∥BC,分别交AB,AC于点D,E.
求证:DE=BD+CE.
例题讲解
证明:∵BO平分∠ABC,
∴∠ABO=∠CBO.
∵DE∥BC,
∴∠CBO=∠DOB.
∴∠ABO=∠DOB.∴BD=OD.
同理可证OE=CE,
∴DE=OD+OE=BD+CE.
三角形的角平分线的应用
知识点二
例3 如图,在△ABC 中. AC = BC,∠C = 90°,AD 是△ABC 的角平分线,DE⊥AB,垂足为 E.
(1)已知 CD = 4 cm,求 AC 的长;
(2)求证:AB = AC + CD.
A
C
B
E
D
解(1):∵AD是△ABC的角平分线,DC丄AC,DE丄AB垂足为E,
∴ DE=CD=4 cm (角平分线上的点到这个角的两边的距离相等).
∵AC=BC,
∴ ∠B=∠BAC, (等边对等角).
∵ ∠C=90°,
∴∠BDE=90°-45°=45° .
∴ BE=DE(等角对等边). 在等腰直角三角形BDE中,
∴ AC=BC=CD+BD=
(2)证明:由(1)的求解过程可知,
Rt△ACD ≌ Rt△AED(HL)
∴AC = AE(全等三角形的对应边相等).
∵BE = DE = CD,
∴AB = AE + BE = AC + CD.
1 在△ABC内到三条边距离相等的点是△ABC的( )
A.三条中线的交点 B.三条角平分线的交点
C.三条高的交点 D.以上均不对
课堂练习
2 到三角形三边距离相等的点的个数是( )
A.1 B.2
C.3 D.4
3 已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB.下列确定P点的方法正确的是( )
A.P为∠A与∠B的平分线的交点
B.P为∠A的平分线与AB的垂直平分线的交点
C.P为AC,AB两边上的高的交点
D.P为AC,AB两边的垂直平分线的交点
4 已知:如图,在 Rt△ACB 中,∠ACB =90°, ∠B = 40°, AD 平分∠CAB 交 BC 于 D 点, DE⊥AB 于 E,则∠CAD = ________.
A
C
B
D
E
E
D
A
B
C
5 如图,在△ABC中,已知AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)如果CD=4cm,AC的长;
(2)求证:AB=AC+CD.
本节课我们利用角平分线的性质和判定定理证明了三角形三条角平分线交于一点,且这一点到三角形各边的距离相等.并综合运用我们前面学过的性质定理等解决了几何中的计算和证明问题.
课堂小结
谢谢聆听
(第2课时)
第一章 三角形的证明
2020-2021北师大版八年级数学下册
1 证明三角形的三条角平分线交于一点.
2 应用角平分线定理解决数学问题.
学习目标
角平分线的性质与判定的内容是什么?
定理 角平分线上的点到这个角的两边的距离相等.
定理 在一个角的内部,到角的两边距离相等的点在这个角的 平分线上.
新课导入
角平分线的性质
知识点一
作三角形的三个内角的角平分线,你发现了什么?
发现:三角形的三个内角的角平分线交于一点,并且这一点到三角形三边的距离相等.
探究新知
例1 求证:三角形三条角平分线相交于一点,并且这一点到三条边的距离相等.
已知:如图,在△ABC 中,角平分线 BM 与角平分线 CN 相交于点 P,过点 P 分别作 AB,BC,AC 的垂线,垂足分别为 D,E,F.
求证:P 点在∠BAC 的角平分线上.
A
B
C
P
E
F
M
D
N
例题讲解
证明∵BM是△ABC的角平分线,点P在BM上,且
PD丄AB,PE丄BC,垂足分别为D,E,
∴PD=PE (角平分线上的点到这个角的两边的距离相等).
同理,PE=PF.
∴PD=PE=PF.
∴点P在∠A的平分线上(在一个角的内部,到角的两边距离相等的点在这个角的平分线上),
即∠A的平分线经过点P.
三角形的三条角平分线相交于一点,并且这一点到三角形三条边的距离相等.
三边垂直平分线
三条角平分线
三角形
锐角三角形
交于三角形内一点
交于三角形内一点
钝角三角形
交于三角形外一点
直角三角形
交于斜边的中点
交点性质
到三角形三个顶点的距离相等
到三角形三边的距离相等
例2 如图,在△ABC中,∠ABC与∠ACB的平分线相交于点O,过点O作DE∥BC,分别交AB,AC于点D,E.
求证:DE=BD+CE.
例题讲解
证明:∵BO平分∠ABC,
∴∠ABO=∠CBO.
∵DE∥BC,
∴∠CBO=∠DOB.
∴∠ABO=∠DOB.∴BD=OD.
同理可证OE=CE,
∴DE=OD+OE=BD+CE.
三角形的角平分线的应用
知识点二
例3 如图,在△ABC 中. AC = BC,∠C = 90°,AD 是△ABC 的角平分线,DE⊥AB,垂足为 E.
(1)已知 CD = 4 cm,求 AC 的长;
(2)求证:AB = AC + CD.
A
C
B
E
D
解(1):∵AD是△ABC的角平分线,DC丄AC,DE丄AB垂足为E,
∴ DE=CD=4 cm (角平分线上的点到这个角的两边的距离相等).
∵AC=BC,
∴ ∠B=∠BAC, (等边对等角).
∵ ∠C=90°,
∴∠BDE=90°-45°=45° .
∴ BE=DE(等角对等边). 在等腰直角三角形BDE中,
∴ AC=BC=CD+BD=
(2)证明:由(1)的求解过程可知,
Rt△ACD ≌ Rt△AED(HL)
∴AC = AE(全等三角形的对应边相等).
∵BE = DE = CD,
∴AB = AE + BE = AC + CD.
1 在△ABC内到三条边距离相等的点是△ABC的( )
A.三条中线的交点 B.三条角平分线的交点
C.三条高的交点 D.以上均不对
课堂练习
2 到三角形三边距离相等的点的个数是( )
A.1 B.2
C.3 D.4
3 已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB.下列确定P点的方法正确的是( )
A.P为∠A与∠B的平分线的交点
B.P为∠A的平分线与AB的垂直平分线的交点
C.P为AC,AB两边上的高的交点
D.P为AC,AB两边的垂直平分线的交点
4 已知:如图,在 Rt△ACB 中,∠ACB =90°, ∠B = 40°, AD 平分∠CAB 交 BC 于 D 点, DE⊥AB 于 E,则∠CAD = ________.
A
C
B
D
E
E
D
A
B
C
5 如图,在△ABC中,已知AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)如果CD=4cm,AC的长;
(2)求证:AB=AC+CD.
本节课我们利用角平分线的性质和判定定理证明了三角形三条角平分线交于一点,且这一点到三角形各边的距离相等.并综合运用我们前面学过的性质定理等解决了几何中的计算和证明问题.
课堂小结
谢谢聆听
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
