北师大版六年级下册数学:1.3圆柱的体积(含答案)
文档属性
| 名称 | 北师大版六年级下册数学:1.3圆柱的体积(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 52.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-07 14:13:37 | ||
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
1.3圆柱的体积
一、单选题
1.计算做一个圆柱形烟囱需要多少铁皮,就是求它的(?
?)。
A.?底面积???????????????????????????????B.?侧面积???????????????????????????????C.?底面积和侧面积之和
2.求做一个圆柱形铁皮油桶要用多少铁皮,需要计算这个圆柱的(??
)
A.?体积???????????????????????????????????????B.?表面积???????????????????????????????????????C.?侧面积
3.下面圆柱体(单位:厘米)的侧面积是(??
)
A.?72.8平方厘米?????????????????B.?62.8平方厘米?????????????????C.?75.36平方厘米?????????????????D.?125.6平方厘米
4.下面的说法错误的有(???
)句。
①圆柱的底面积与高都扩大3倍,它的体积就扩大6倍。
②既是2的倍数又是5的倍数的数的特征是个位必须是0。
③一条线段绕着它的一个端点旋转120°,形成的图形是
圆。
④在长方体上,我们找不到两条既不平行也不相交的线段。
⑤公式S梯=(a+b)h÷2,当a=b时,就是平行四边形的面积计算公式。
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
5.做一个底面半径10cm,高30cm的圆柱形纸盒,至少需要用多大面积的纸板?(接口处不计)(??
)
A.?1884平方厘米??????????????????????????B.?2512平方厘米??????????????????????????C.?628平方厘米
二、判断题
6.圆柱的体积一般比它的表面积大。
7.把一个棱长6cm正方体切成两个同样的长方体,表面积增加12平方厘米。
8.圆柱的底面积扩大3倍,体积就扩大3倍。
9.一个圆柱,底面半径为r,高是2πr.这个圆柱的侧面展开图是一个正方形.
三、填空题
10.计算出下列圆柱的侧面积.
侧面积是________?
?
11.填空
圆柱的表面积=________×2+________.
圆柱的侧面积=________×________.
12.体育馆里的圆柱形状的柱子,底面周长2.5米,高5.2米.如果在柱子的侧面涂上油漆,每根柱子涂油漆的面积是________平方米?
13.有一根粗细均匀的圆柱形木料,长2米,根据需要,现把它锯成长1米的两根圆柱形木料后,表面积增加了628平方厘米.这根木料原来的体积是________立方厘米.
14.把一张长6分米、宽4分米的长方形纸片卷成一个圆柱,这个圆柱的最大容积是________。(π取3)
四、解答题
15.计算下面圆柱的表面积.
16.如下图所示,把底面直径为8厘米的圆柱切成若干等份,拼成一个近似的长方体。这个长方体的表面积比原来增加80平方厘米,那么圆柱的体积是多少立方厘米?
五、综合题
17.一个圆柱形游泳池,底面周长为62.8米,深2米。
(1)在池内侧面和池底抹上水泥,抹水泥的面积多少平方米?
(2)水面离池口0.5米,这时池里的水有多少立方米?
六、应用题
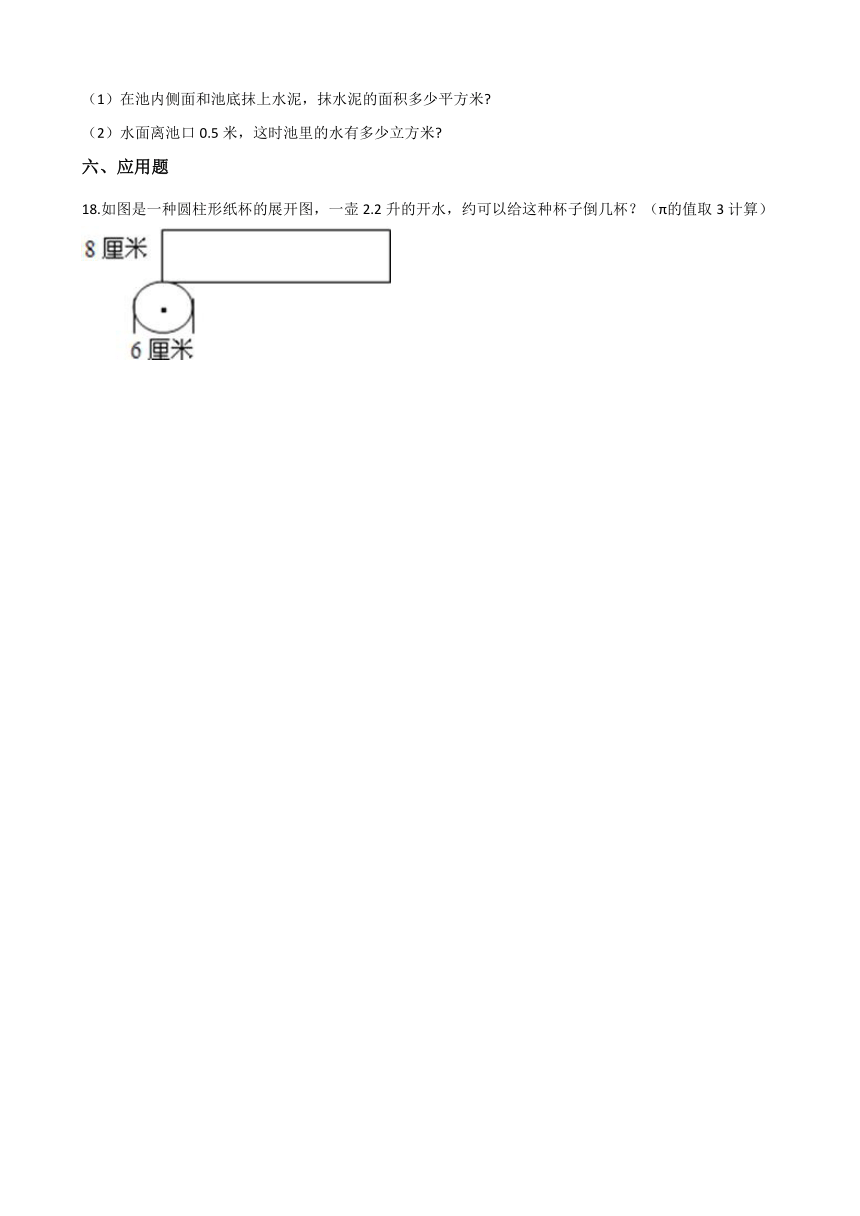
18.如图是一种圆柱形纸杯的展开图,一壶2.2升的开水,约可以给这种杯子倒几杯?(π的值取3计算)
参考答案
一、单选题
1.【答案】B
【解析】【解答】解:烟囱是不需要两个底的,所以计算做一个圆柱形烟囱需要多少铁皮,就是求它的侧面积。
故答案为:B。
【分析】烟囱是不需要两个底的。
2.【答案】B
【解析】【解答】根据圆柱的表面积知识可知,求做一个圆柱形铁皮油桶要用的铁皮面积就是求这个圆柱的表面积.
故答案为:B
【分析】求需要铁皮的面积就是这个油桶的两个底面积与侧面积的和,也就是圆柱形油桶的表面积.
3.【答案】
B
【解析】【解答】3.14×10×2
=3.14×20
=62.8(平方厘米)
故答案为:B
【分析】圆柱的侧面展开后是一个长方形或正方形,长方形或正方形的一条边与圆柱的底面周长相等,相邻的另一条边与高相等,用底面周长乘高即可求出圆柱的侧面积.
4.【答案】
B
【解析】【解答】解:①圆柱的底面积与高都扩大3倍,它的体积就扩大9倍;原来说法错误;
②既是2的倍数又是5的倍数的数的特征是个位必须是0。原来说法正确;
③120÷360=,
原来说法正确;
④在长方体上,例如前面长方形下面的长与后面长方形的宽就不平行也不相交。原来说法错误;
⑤a=b时,说明上底和下底相等,那么这个图形实际就是一个平行四边形,就是平行四边形的面积计算公式。原来说法正确。
故答案为:B。
【分析】①圆柱的体积=底面积×高,因此体积扩大的倍数是3×3=9;
④长方体相对面不对应的长和宽既不平行也不相交。
5.【答案】
B
【解析】【解答】需要纸板的面积就是圆柱形纸盒的侧面积+2个底面面积之和,即:
2×3.14×10×30+3.14×10?×2
=1884+628
=2512(平方厘米)
故选:B
【分析】需要纸板的面积就是圆柱形纸盒的表面积,求表面积可用S=2πr
h+2πr?解答。
二、判断题
6.【答案】
错误
【解析】【解答】解:圆柱的体积和表面积无法比较大小,原题说法错误。
故答案为:错误。
【分析】体积是物体所占空间的大小,表面积是物体表面的面积之和,体积和表面积的意义不同,无法比较大小。
7.【答案】
错误
【解析】【解答】6×6×2=72(平方厘米)
答:表面积将增加72平方厘米.
故答案为:错误
【分析】把正方体切成完全一样的两个长方体后,它的表面积比原来增加了2个正方体的面的面积,由此即可解答问题。
8.【答案】
错误
【解析】【解答】如果高不变,则圆柱的体积与底面积成正比例,底面积扩大3倍,则体积扩大3倍,但是原题没有说明圆柱的高,所以原题说法错误。
故答案为:错误
【分析】圆柱的体积=底面积×高,如果高不变,则圆柱的体积与底面积成正比例,底面积扩大3倍,则体积扩大3倍,由此即可判断.
9.【答案】
正确
【解析】【解答】圆柱的底面周长是:C=2πr,高也是2πr,当底面周长和高相等时,侧面展开图是一个正方形,原题说法正确.
故答案为:正确.
【分析】已知圆柱的底面半径是r,圆柱的底面周长是:C=2πr,然后对比底面周长和高,据此解答.
三、填空题
10.【答案】
301.44
【解析】【解答】3.14×24×4
=3.14×96
=301.44(cm?)
故答案为:301.44
【分析】圆柱的侧面积=底面周长×高,由此根据圆柱的侧面积公式计算侧面积即可.
11.【答案】
底面的面积;圆柱的侧面积;底面周长;高
【解析】【解答】根据圆柱的组成可知,圆柱的表面积=底面的面积×2+圆柱的侧面积;圆柱的侧面积=底面周长×高.
故答案为:底面的面积;圆柱的侧面积;底面周长;高
【分析】圆柱由两个相同的圆形的面和一个曲面组成,两个圆形的底面就是底面积,一个曲面是圆柱的侧面;圆柱的表面积就是两个底面的面积之和加上侧面的面积.
12.【答案】
13
【解析】【解答】2.5×5.2=13(平方米)
【分析】此题重点考查圆柱体的侧面积公式s=ch的掌握与运用情况,解答此题应注意分清求的是几个面的面积,据此列式计算即可。
13.【答案】
62800
【解析】【解答】解:2米=200厘米,
628÷2×200,
=314×200,
=62800(立方厘米).
答:这根木料的体积是62800立方厘米.
故答案为:62800.
【分析】把一根长2米的圆柱形木料截成两段,表面积比原来增加了2个横截面,求出横截面,再根据圆柱的体积公式求出它的体积.据此解答.本题的关键是把圆柱形木料截成两段,表面积比原来增加了2个横截面.
14.【答案】
12立方分米
【解析】【解答】解:(6÷3÷2)2×3×4=12立方分米;(4÷3÷2)2×3×6=8立方分米,所以这个圆柱的最大容积是12立方分米。
故答案为:12立方分米。
【分析】将这张纸卷成一个圆柱有2种情况,一种情况就是长做底边,那么圆柱的容积=(长方形的长÷π÷2)2×π×长方形的宽;另一种情况就是宽做底边,那么圆柱的容积=(长方形的宽÷π÷2)2×π×长方形的长。然后进行比较即可。
四、解答题
15.【答案】解:3.14×4×10+3.14×(4÷2)2×2
=125.6+25.12
=150.72(平方厘米)
答:圆柱的表面积是150.72平方厘米。
【解析】【分析】根据圆柱的表面积=侧面积+底面积×2=2πrh+2πr2
,
据此代入数据即可解答。
16.【答案】
解:高:80÷2÷(8÷2)=10(厘米)
体积:3.14×(8÷2)2×10=502.4(立方厘米)
答:那么圆柱的体积是502.4立方厘米。
【解析】【分析】根据题意可知,把底面直径为8厘米的圆柱切成若干等份,拼成一个近似的长方体,这个长方体的表面积比原来增加两个面的面积,这两个面的长是圆柱的高,宽是圆柱的底面半径,要求圆柱的高,用增加的表面积÷2÷圆柱的底面半径=圆柱的高;然后用公式:圆柱的体积V=πr2h,据此列式解答.
五、综合题
17.【答案】(1)解:62.8÷3.14÷2=10(米)
3.14×10?+62.8×2
=314+125.6
=439.6(平方米)
答:抹水泥的面积是439.6平方米。
(2)解:3.14×10?×(2-0.5)
=314×1.95
=612.3(立方米)
答:这时池里的水有612.3立方米。
【解析】【分析】(1)用底面周长除以3.14再除以2求出底面半径,用底面积加上侧面积就是抹水泥部分的面积;(2)用底面积乘水面的高度即可求出水的体积。
六、应用题
18.【答案】解:纸杯的底面半径为:6÷2=3(厘米),
纸杯的容积为:3×32×8
=27×8,
=216(立方厘米),
216立方厘米=0.216立方分米=0.216升,
2.2÷0.216≈10(杯);
答:约可以给这种杯子倒10杯水。
【解析】【分析】根据题意,可根据圆柱的体积公式V=底面积×高计算出这个纸杯的容积,然后再用2.2升的水除以杯子的容积即可得到可用倒的杯数,列式解答即可得到答案。
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
1.3圆柱的体积
一、单选题
1.计算做一个圆柱形烟囱需要多少铁皮,就是求它的(?
?)。
A.?底面积???????????????????????????????B.?侧面积???????????????????????????????C.?底面积和侧面积之和
2.求做一个圆柱形铁皮油桶要用多少铁皮,需要计算这个圆柱的(??
)
A.?体积???????????????????????????????????????B.?表面积???????????????????????????????????????C.?侧面积
3.下面圆柱体(单位:厘米)的侧面积是(??
)
A.?72.8平方厘米?????????????????B.?62.8平方厘米?????????????????C.?75.36平方厘米?????????????????D.?125.6平方厘米
4.下面的说法错误的有(???
)句。
①圆柱的底面积与高都扩大3倍,它的体积就扩大6倍。
②既是2的倍数又是5的倍数的数的特征是个位必须是0。
③一条线段绕着它的一个端点旋转120°,形成的图形是
圆。
④在长方体上,我们找不到两条既不平行也不相交的线段。
⑤公式S梯=(a+b)h÷2,当a=b时,就是平行四边形的面积计算公式。
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
5.做一个底面半径10cm,高30cm的圆柱形纸盒,至少需要用多大面积的纸板?(接口处不计)(??
)
A.?1884平方厘米??????????????????????????B.?2512平方厘米??????????????????????????C.?628平方厘米
二、判断题
6.圆柱的体积一般比它的表面积大。
7.把一个棱长6cm正方体切成两个同样的长方体,表面积增加12平方厘米。
8.圆柱的底面积扩大3倍,体积就扩大3倍。
9.一个圆柱,底面半径为r,高是2πr.这个圆柱的侧面展开图是一个正方形.
三、填空题
10.计算出下列圆柱的侧面积.
侧面积是________?
?
11.填空
圆柱的表面积=________×2+________.
圆柱的侧面积=________×________.
12.体育馆里的圆柱形状的柱子,底面周长2.5米,高5.2米.如果在柱子的侧面涂上油漆,每根柱子涂油漆的面积是________平方米?
13.有一根粗细均匀的圆柱形木料,长2米,根据需要,现把它锯成长1米的两根圆柱形木料后,表面积增加了628平方厘米.这根木料原来的体积是________立方厘米.
14.把一张长6分米、宽4分米的长方形纸片卷成一个圆柱,这个圆柱的最大容积是________。(π取3)
四、解答题
15.计算下面圆柱的表面积.
16.如下图所示,把底面直径为8厘米的圆柱切成若干等份,拼成一个近似的长方体。这个长方体的表面积比原来增加80平方厘米,那么圆柱的体积是多少立方厘米?
五、综合题
17.一个圆柱形游泳池,底面周长为62.8米,深2米。
(1)在池内侧面和池底抹上水泥,抹水泥的面积多少平方米?
(2)水面离池口0.5米,这时池里的水有多少立方米?
六、应用题
18.如图是一种圆柱形纸杯的展开图,一壶2.2升的开水,约可以给这种杯子倒几杯?(π的值取3计算)
参考答案
一、单选题
1.【答案】B
【解析】【解答】解:烟囱是不需要两个底的,所以计算做一个圆柱形烟囱需要多少铁皮,就是求它的侧面积。
故答案为:B。
【分析】烟囱是不需要两个底的。
2.【答案】B
【解析】【解答】根据圆柱的表面积知识可知,求做一个圆柱形铁皮油桶要用的铁皮面积就是求这个圆柱的表面积.
故答案为:B
【分析】求需要铁皮的面积就是这个油桶的两个底面积与侧面积的和,也就是圆柱形油桶的表面积.
3.【答案】
B
【解析】【解答】3.14×10×2
=3.14×20
=62.8(平方厘米)
故答案为:B
【分析】圆柱的侧面展开后是一个长方形或正方形,长方形或正方形的一条边与圆柱的底面周长相等,相邻的另一条边与高相等,用底面周长乘高即可求出圆柱的侧面积.
4.【答案】
B
【解析】【解答】解:①圆柱的底面积与高都扩大3倍,它的体积就扩大9倍;原来说法错误;
②既是2的倍数又是5的倍数的数的特征是个位必须是0。原来说法正确;
③120÷360=,
原来说法正确;
④在长方体上,例如前面长方形下面的长与后面长方形的宽就不平行也不相交。原来说法错误;
⑤a=b时,说明上底和下底相等,那么这个图形实际就是一个平行四边形,就是平行四边形的面积计算公式。原来说法正确。
故答案为:B。
【分析】①圆柱的体积=底面积×高,因此体积扩大的倍数是3×3=9;
④长方体相对面不对应的长和宽既不平行也不相交。
5.【答案】
B
【解析】【解答】需要纸板的面积就是圆柱形纸盒的侧面积+2个底面面积之和,即:
2×3.14×10×30+3.14×10?×2
=1884+628
=2512(平方厘米)
故选:B
【分析】需要纸板的面积就是圆柱形纸盒的表面积,求表面积可用S=2πr
h+2πr?解答。
二、判断题
6.【答案】
错误
【解析】【解答】解:圆柱的体积和表面积无法比较大小,原题说法错误。
故答案为:错误。
【分析】体积是物体所占空间的大小,表面积是物体表面的面积之和,体积和表面积的意义不同,无法比较大小。
7.【答案】
错误
【解析】【解答】6×6×2=72(平方厘米)
答:表面积将增加72平方厘米.
故答案为:错误
【分析】把正方体切成完全一样的两个长方体后,它的表面积比原来增加了2个正方体的面的面积,由此即可解答问题。
8.【答案】
错误
【解析】【解答】如果高不变,则圆柱的体积与底面积成正比例,底面积扩大3倍,则体积扩大3倍,但是原题没有说明圆柱的高,所以原题说法错误。
故答案为:错误
【分析】圆柱的体积=底面积×高,如果高不变,则圆柱的体积与底面积成正比例,底面积扩大3倍,则体积扩大3倍,由此即可判断.
9.【答案】
正确
【解析】【解答】圆柱的底面周长是:C=2πr,高也是2πr,当底面周长和高相等时,侧面展开图是一个正方形,原题说法正确.
故答案为:正确.
【分析】已知圆柱的底面半径是r,圆柱的底面周长是:C=2πr,然后对比底面周长和高,据此解答.
三、填空题
10.【答案】
301.44
【解析】【解答】3.14×24×4
=3.14×96
=301.44(cm?)
故答案为:301.44
【分析】圆柱的侧面积=底面周长×高,由此根据圆柱的侧面积公式计算侧面积即可.
11.【答案】
底面的面积;圆柱的侧面积;底面周长;高
【解析】【解答】根据圆柱的组成可知,圆柱的表面积=底面的面积×2+圆柱的侧面积;圆柱的侧面积=底面周长×高.
故答案为:底面的面积;圆柱的侧面积;底面周长;高
【分析】圆柱由两个相同的圆形的面和一个曲面组成,两个圆形的底面就是底面积,一个曲面是圆柱的侧面;圆柱的表面积就是两个底面的面积之和加上侧面的面积.
12.【答案】
13
【解析】【解答】2.5×5.2=13(平方米)
【分析】此题重点考查圆柱体的侧面积公式s=ch的掌握与运用情况,解答此题应注意分清求的是几个面的面积,据此列式计算即可。
13.【答案】
62800
【解析】【解答】解:2米=200厘米,
628÷2×200,
=314×200,
=62800(立方厘米).
答:这根木料的体积是62800立方厘米.
故答案为:62800.
【分析】把一根长2米的圆柱形木料截成两段,表面积比原来增加了2个横截面,求出横截面,再根据圆柱的体积公式求出它的体积.据此解答.本题的关键是把圆柱形木料截成两段,表面积比原来增加了2个横截面.
14.【答案】
12立方分米
【解析】【解答】解:(6÷3÷2)2×3×4=12立方分米;(4÷3÷2)2×3×6=8立方分米,所以这个圆柱的最大容积是12立方分米。
故答案为:12立方分米。
【分析】将这张纸卷成一个圆柱有2种情况,一种情况就是长做底边,那么圆柱的容积=(长方形的长÷π÷2)2×π×长方形的宽;另一种情况就是宽做底边,那么圆柱的容积=(长方形的宽÷π÷2)2×π×长方形的长。然后进行比较即可。
四、解答题
15.【答案】解:3.14×4×10+3.14×(4÷2)2×2
=125.6+25.12
=150.72(平方厘米)
答:圆柱的表面积是150.72平方厘米。
【解析】【分析】根据圆柱的表面积=侧面积+底面积×2=2πrh+2πr2
,
据此代入数据即可解答。
16.【答案】
解:高:80÷2÷(8÷2)=10(厘米)
体积:3.14×(8÷2)2×10=502.4(立方厘米)
答:那么圆柱的体积是502.4立方厘米。
【解析】【分析】根据题意可知,把底面直径为8厘米的圆柱切成若干等份,拼成一个近似的长方体,这个长方体的表面积比原来增加两个面的面积,这两个面的长是圆柱的高,宽是圆柱的底面半径,要求圆柱的高,用增加的表面积÷2÷圆柱的底面半径=圆柱的高;然后用公式:圆柱的体积V=πr2h,据此列式解答.
五、综合题
17.【答案】(1)解:62.8÷3.14÷2=10(米)
3.14×10?+62.8×2
=314+125.6
=439.6(平方米)
答:抹水泥的面积是439.6平方米。
(2)解:3.14×10?×(2-0.5)
=314×1.95
=612.3(立方米)
答:这时池里的水有612.3立方米。
【解析】【分析】(1)用底面周长除以3.14再除以2求出底面半径,用底面积加上侧面积就是抹水泥部分的面积;(2)用底面积乘水面的高度即可求出水的体积。
六、应用题
18.【答案】解:纸杯的底面半径为:6÷2=3(厘米),
纸杯的容积为:3×32×8
=27×8,
=216(立方厘米),
216立方厘米=0.216立方分米=0.216升,
2.2÷0.216≈10(杯);
答:约可以给这种杯子倒10杯水。
【解析】【分析】根据题意,可根据圆柱的体积公式V=底面积×高计算出这个纸杯的容积,然后再用2.2升的水除以杯子的容积即可得到可用倒的杯数,列式解答即可得到答案。
