5.1.1 相交线 课件(共17张PPT)
文档属性
| 名称 | 5.1.1 相交线 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-06 00:00:00 | ||
图片预览





文档简介
5.1.1 相交线
第五章 相交线与平行线
2021年春人教版七年级数学下册
1、在具体的情境和图片中找出相交线。
2、理解邻补角和对顶角的概念。
3、探索相交线对顶角之间的关系。
理解邻补角和对顶角的概念。(重点)
探索相交线对顶角之间的关系。(难点)
学习目标
新课导入
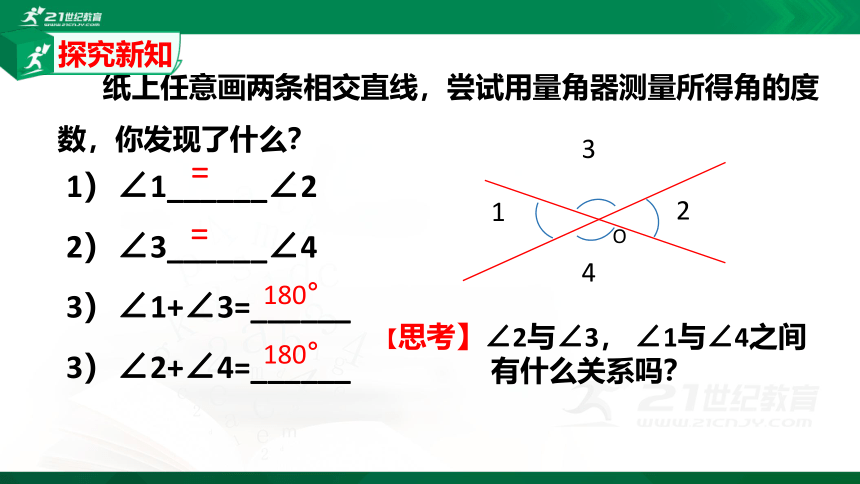
纸上任意画两条相交直线,尝试用量角器测量所得角的度数,你发现了什么?
1
2
3
4
1)∠1______∠2
2)∠3______∠4
3)∠1+∠3=______
3)∠2+∠4=______
=
=
180°
180°
O
【思考】∠2与∠3, ∠1与∠4之间有什么关系吗?
探究新知
如果两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角。
1
2
3
4
【想一想】∠1与那个角互为邻补角?∠2呢?
探究新知
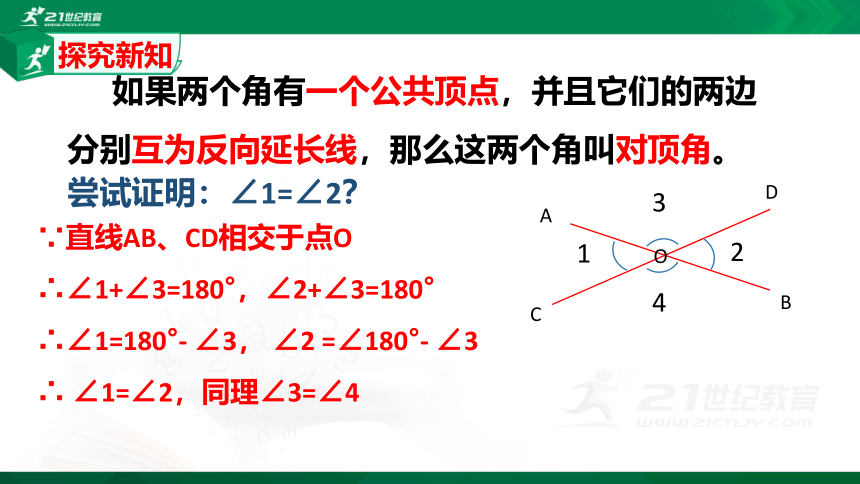
如果两个角有一个公共顶点,并且它们的两边分别互为反向延长线,那么这两个角叫对顶角。
尝试证明:∠1=∠2?
∵直线AB、CD相交于点O
∴∠1+∠3=180°,∠2+∠3=180°
∴∠1=180°- ∠3, ∠2 =∠180°- ∠3
∴ ∠1=∠2,同理∠3=∠4
1
2
3
4
D
A
B
C
对顶角的性质:对顶角相等
O
探究新知
名称
特征
性质
相同点
不同点
对顶角
邻补角
1.两条直线相交而成的角
2.有一个公共顶点
3.没有公共边
1.两条直线相交而成的角
2.有一个公共顶点
3.有一条公共边
对顶角
相等
邻补角
互补
由两条直线相交
而成的角,
都有一个
公共顶点,
他们都成
对出现
1.对顶角没有公共边,邻补角有一条公共边。
2.两条直线相交时,一个角的对顶角有一个,而一个角的邻补角有两个。
总结归纳
1、当∠1=35°时,求∠2,∠3,∠ 4的度数;
1
2
3
4
解:1)由邻补角的定义,得
∠3=180°-∠1=180°-35°=145°
由对顶角的性质,得
∠2 =∠1 =35°
∠3 =∠4 =145°
课堂练习
2.当∠1=n°时,求∠2,∠3,∠4的度数;
1
2
3
4
解:由邻补角的定义,得
∠3=180°-∠1=180°- n°
由对顶角的性质,得
∠2 =∠1 = n°
∠3 =∠4 =180°- n°
3.当∠3是∠1的5倍时, 求∠1,∠2,∠3,∠4的度数;
1
2
3
4
解:由邻补角的定义,得
∠3+∠1=180°而∠3是∠1的5倍
解得,∠1=30°,∠3=150°
由对顶角的性质,得
∠2 =∠1 =30°
∠3 =∠4 =150°
4.如图,直线AC和直线BD相交于点O,若∠1+∠2=90°,则∠BOC的度数是( ??)
A.100° B.115°
C.135° D.145°
【答案】C
【详解】
解:∵∠1=∠2,∠1+∠2=90°,
∴∠1=∠2=45°,
∴∠BOC=135°,
故选C.
5.如图,直线AB、CD相交于点O,OE平分∠DOB,若∠AOC=40?,求∠AOE的度数.
解:∵∠AOC=40°,
∴∠AOD=180°?∠AOC=140°,∠DOB=∠AOC=40°,
∵OE平分∠DOB,
∴∠DOE=12∠DOB=20°,
∴∠AOE=∠AOD+∠DOE=140°+20°=160°.
?
6.直线AB、CD、EF交于点O,则∠1+∠2+∠3=_____度.
【答案】180
【详解】
解:如图,∠BOD=∠1,
∵∠2+∠3+∠BOD=180°,
∴∠1+∠2+∠3=180°.
故答案为:180
7.直线AB、CD相交于点O,OE⊥AB于O,且∠DOB=2∠COE,求∠AOD的度数.
解:∵∠EOB=90°
∴∠DOB+∠COE=90°
又∵∠DOB是∠EOC的两倍,
∴∠EOC=30°
∴∠AOD=∠BOC=∠EOC+∠BOE=30°+90°=120°
8.如图所示,已知直线AB和CD相交于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°.
(1)求∠AON的度数.
(2)写出∠DON的余角.
(1)∵∠AOC+∠AOD=∠AOD+∠BOD=180°,∴∠BOD=∠AOC=50°,
∵OM平分∠BOD,∴∠BOM=∠DOM=25°,又由∠MON=90°,
∴∠AON=180°﹣(∠MON+∠BOM)=180°﹣(90°+25°)=65°;
(2)由∠DON+∠DOM=∠MON=90°知∠DOM为∠DON的余角,
∵∠AON+∠BOM=90°,∠DOM=∠MOB,
∴∠AON+∠DOM=90°,
∴∠NOD+∠BOM=90°,
故∠DON的余角为:∠DOM,∠BOM.
谢谢聆听
第五章 相交线与平行线
2021年春人教版七年级数学下册
1、在具体的情境和图片中找出相交线。
2、理解邻补角和对顶角的概念。
3、探索相交线对顶角之间的关系。
理解邻补角和对顶角的概念。(重点)
探索相交线对顶角之间的关系。(难点)
学习目标
新课导入
纸上任意画两条相交直线,尝试用量角器测量所得角的度数,你发现了什么?
1
2
3
4
1)∠1______∠2
2)∠3______∠4
3)∠1+∠3=______
3)∠2+∠4=______
=
=
180°
180°
O
【思考】∠2与∠3, ∠1与∠4之间有什么关系吗?
探究新知
如果两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角。
1
2
3
4
【想一想】∠1与那个角互为邻补角?∠2呢?
探究新知
如果两个角有一个公共顶点,并且它们的两边分别互为反向延长线,那么这两个角叫对顶角。
尝试证明:∠1=∠2?
∵直线AB、CD相交于点O
∴∠1+∠3=180°,∠2+∠3=180°
∴∠1=180°- ∠3, ∠2 =∠180°- ∠3
∴ ∠1=∠2,同理∠3=∠4
1
2
3
4
D
A
B
C
对顶角的性质:对顶角相等
O
探究新知
名称
特征
性质
相同点
不同点
对顶角
邻补角
1.两条直线相交而成的角
2.有一个公共顶点
3.没有公共边
1.两条直线相交而成的角
2.有一个公共顶点
3.有一条公共边
对顶角
相等
邻补角
互补
由两条直线相交
而成的角,
都有一个
公共顶点,
他们都成
对出现
1.对顶角没有公共边,邻补角有一条公共边。
2.两条直线相交时,一个角的对顶角有一个,而一个角的邻补角有两个。
总结归纳
1、当∠1=35°时,求∠2,∠3,∠ 4的度数;
1
2
3
4
解:1)由邻补角的定义,得
∠3=180°-∠1=180°-35°=145°
由对顶角的性质,得
∠2 =∠1 =35°
∠3 =∠4 =145°
课堂练习
2.当∠1=n°时,求∠2,∠3,∠4的度数;
1
2
3
4
解:由邻补角的定义,得
∠3=180°-∠1=180°- n°
由对顶角的性质,得
∠2 =∠1 = n°
∠3 =∠4 =180°- n°
3.当∠3是∠1的5倍时, 求∠1,∠2,∠3,∠4的度数;
1
2
3
4
解:由邻补角的定义,得
∠3+∠1=180°而∠3是∠1的5倍
解得,∠1=30°,∠3=150°
由对顶角的性质,得
∠2 =∠1 =30°
∠3 =∠4 =150°
4.如图,直线AC和直线BD相交于点O,若∠1+∠2=90°,则∠BOC的度数是( ??)
A.100° B.115°
C.135° D.145°
【答案】C
【详解】
解:∵∠1=∠2,∠1+∠2=90°,
∴∠1=∠2=45°,
∴∠BOC=135°,
故选C.
5.如图,直线AB、CD相交于点O,OE平分∠DOB,若∠AOC=40?,求∠AOE的度数.
解:∵∠AOC=40°,
∴∠AOD=180°?∠AOC=140°,∠DOB=∠AOC=40°,
∵OE平分∠DOB,
∴∠DOE=12∠DOB=20°,
∴∠AOE=∠AOD+∠DOE=140°+20°=160°.
?
6.直线AB、CD、EF交于点O,则∠1+∠2+∠3=_____度.
【答案】180
【详解】
解:如图,∠BOD=∠1,
∵∠2+∠3+∠BOD=180°,
∴∠1+∠2+∠3=180°.
故答案为:180
7.直线AB、CD相交于点O,OE⊥AB于O,且∠DOB=2∠COE,求∠AOD的度数.
解:∵∠EOB=90°
∴∠DOB+∠COE=90°
又∵∠DOB是∠EOC的两倍,
∴∠EOC=30°
∴∠AOD=∠BOC=∠EOC+∠BOE=30°+90°=120°
8.如图所示,已知直线AB和CD相交于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°.
(1)求∠AON的度数.
(2)写出∠DON的余角.
(1)∵∠AOC+∠AOD=∠AOD+∠BOD=180°,∴∠BOD=∠AOC=50°,
∵OM平分∠BOD,∴∠BOM=∠DOM=25°,又由∠MON=90°,
∴∠AON=180°﹣(∠MON+∠BOM)=180°﹣(90°+25°)=65°;
(2)由∠DON+∠DOM=∠MON=90°知∠DOM为∠DON的余角,
∵∠AON+∠BOM=90°,∠DOM=∠MOB,
∴∠AON+∠DOM=90°,
∴∠NOD+∠BOM=90°,
故∠DON的余角为:∠DOM,∠BOM.
谢谢聆听
