七年级数学角的比较和运算
文档属性
| 名称 | 七年级数学角的比较和运算 |  | |
| 格式 | zip | ||
| 文件大小 | 688.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-14 19:51:20 | ||
图片预览









文档简介
(共38张PPT)
你选择从哪一面上山呢?
成功永远属于肯攀高峰的人
D
A
B
C
∠ABC>∠DCB
4.3.2
我们清晰的记得怎么样比较两条线段的长短方法?
即用刻度尺测量线段的
即将其中一条线段移到
3、重叠比较法
2、度量法
1、观察法
长度的方法。
另一条上作比较。
思 考
如何比较下列两个角的大小?
A
O
B
A′
O′
B′
活动一:
请每个学习小组的同学每人任意画出两个角 ,比较这两个角的大小,并
讨论你们的比较方法:
锐角:00<∠β<900
钝角:900< ∠α<1800
1周角>1平角>钝角>1直角>锐角
1平角=1800
1直角=900
1周角=3600
一:观察法
A
B
O
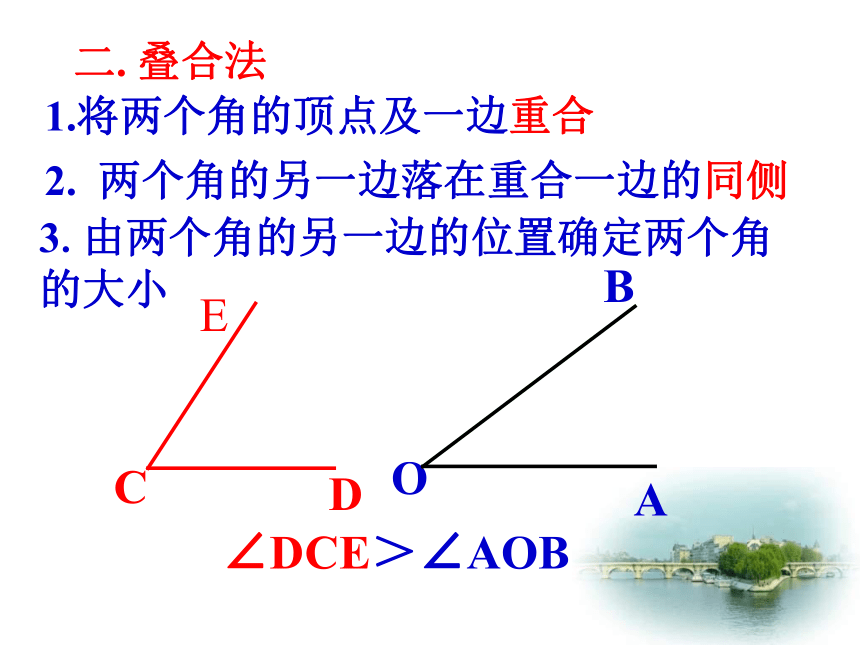
1.将两个角的顶点及一边重合
2. 两个角的另一边落在重合一边的同侧
3.由两个角的另一边的位置确定两个角的大小
二. 叠合法
C
D
E
∠DCE>∠AOB
O
A
B
D
C
E
A
O
B
C
D
E
∠DCE<∠AOB
∠ DCE =∠AOB
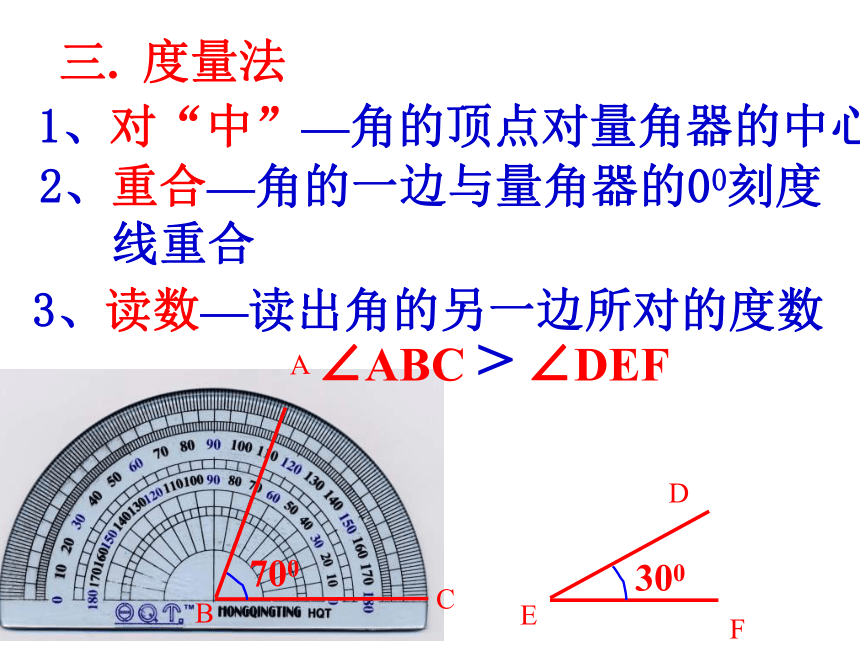
三. 度量法
1、对“中”—角的顶点对量角器的中心
3、读数—读出角的另一边所对的度数
2、重合—角的一边与量角器的00刻度
线重合
B
C
A
F
E
D
700
∠ABC > ∠DEF
300
比较两个角的大小的方法有三种:
观察法
叠合法
度量法
小结:
角的分类
角 锐 角 直角 钝 角 平角 周角
范围
∠β
0°<∠β<90°
90°
90 °<∠β<180 ° 180° 360°
图示
┓
记一记
两个角的大小关系有三种,记作:
(1) ∠ABC > ∠DEF
(2)∠ABC< ∠DEF
(3)∠ABC = ∠DEF
A
D
(E)
(F)
C
B
D
(E)
(F)
A
A
B
C
(E)
(D)
(F)
B
C
估计图中∠1与∠2的大小关系,
1
2
2
1
(1)
(2)
练习:
并用适当的方法检验.
返回
下一张
上一张
退出
观察与思考
角的大小与角的两边画出的长短有关吗?
(1)角的大小与角的两边画出的
长短没有关系。
(2)角张开的程度越小,角度
就越小
结论:
迷人数学世界
用放大镜看蚂蚁,用放大镜看自己的手,用放大镜看精致的邮票,用放大镜从太阳光里取火等 等,都会得到令人开心的结果。那么,有没有放大镜放不大的事物呢?
你知道放大镜不能“放大”角
的度数的原因吗?
三. 角的和与差
B
C
A
700
F
E
D
300
因为∠ABC = 700 ,∠DEF=300,
所以∠ABC —∠DEF
=700—300
=400
所以∠ABC — ∠DEF
=∠ABD
⌒
2
⌒
1
∠2= ∠1+∠3
∠3= ∠2- ∠1
∠1= ∠2-∠3
三. 角的和差
3
⌒
观 察
如图,
O
A
B
C
∠AOC是 ∠AOB与 ∠BOC的和
∠AOB是∠AOC与∠BOC的差
记作:∠AOC= ∠AOB+ ∠BOC
记作:∠AOB=∠AOC—∠BOC
类似有∠BOC= ∠AOC—∠AOB
图中共有几个角?它们之间有什么关系?
D
O
B
C
A
练习2, 如图:
∠ AOC = ( ) + ( )
= ( ) - ( )
∠ BOC=( ) - ( )
= ( ) - ( )
∠ AOB
∠ BOC
∠ AOD
∠ COD
∠ COD
∠ BOD
∠ AOC
∠ AOB
如图∠ AOB= ∠ COD=900,
∠ AOD=1460, ∠ BOC= ;
340
D
练习3
A
B
C
D
E
1
2
⌒
⌒
图中∠1= ∠2, 试判断∠BAD和∠EAC的大小, 并说明理由.
冲击
解: ∠BAD= ∠2+ ∠DCA
∠EAC= ∠1+∠DCA
做一做
在纸上任意画一个角∠AOB,
把它对折,使角的两边OA与
OB重合,然后展开、铺平,
画出折痕OC。
则∠AOC与∠BOC有什么大小
关系?
A
O
B
C
角的平分线:从一个角的顶点引出的一条射线,
把这个角分成两个相等的角。
这条射线叫这个角的平分线。
如果给你任意一个角∠AOB,
你有什么方法画出它的平分线?
想一想
A
O
B
学一学
D
P
例2 如图 ∠ABC=90°,∠CBD=30°,
BP平分∠ABD。求∠ABP的度数。
A
B
C
探究:
借助一个三角尺可以画出哪些度数的角,用一副三角尺你还能画出哪些度数的角 上台来展示你的结果。
75°
15°
105 °
15°
120°
小结:
1、角的大小比较方法:
4、三角板可拼出哪些角?
3、角的和差计算
2、角的大小关系有哪些?
数一数:图中共有几个小于平角的角,找出规律。
O
A
B
C
D
O
B
C
A
(1)
(2)
1
2
3
O
A
B
C
D
E
F
O
A
B
C
D
E
(3)
(4)
……
如果以o为端点,有n条射线,那么组
成的角有多少个?
共有(n-1)+(n-2)+(n-3)+…+3+2+1=
n(n-1)/2
已知∠AOB=145°和∠AOC=25°
则∠BOC= 。
练一练
分类
思想
★★
练一练
2. 如图,OC是∠AOB的任意一条射线,
OD平分∠AOC,OE平分∠BOC。
问∠DOE与∠AOB有什么关系?
C
D
E
★★
A
B
O
3. 如图,∠AOB=64°,
OA1平分∠AOB,
OA2平分∠AOA1,
OA3平分∠AOA2,
OA4平分∠AOA3,
则∠AOA4= .
A
O
B
A1
A2
A3
A4
★★
练一练
如图所示的正方形网格中, ∠ 1 + ∠ 2 + ∠ 3+ ∠ 4+ ∠ 5+ ∠ 6+ ∠ 7= 。
1
2
3
4
5
6
7
试一试
作业:
课本144页10题
谢谢!!!!
你选择从哪一面上山呢?
成功永远属于肯攀高峰的人
D
A
B
C
∠ABC>∠DCB
4.3.2
我们清晰的记得怎么样比较两条线段的长短方法?
即用刻度尺测量线段的
即将其中一条线段移到
3、重叠比较法
2、度量法
1、观察法
长度的方法。
另一条上作比较。
思 考
如何比较下列两个角的大小?
A
O
B
A′
O′
B′
活动一:
请每个学习小组的同学每人任意画出两个角 ,比较这两个角的大小,并
讨论你们的比较方法:
锐角:00<∠β<900
钝角:900< ∠α<1800
1周角>1平角>钝角>1直角>锐角
1平角=1800
1直角=900
1周角=3600
一:观察法
A
B
O
1.将两个角的顶点及一边重合
2. 两个角的另一边落在重合一边的同侧
3.由两个角的另一边的位置确定两个角的大小
二. 叠合法
C
D
E
∠DCE>∠AOB
O
A
B
D
C
E
A
O
B
C
D
E
∠DCE<∠AOB
∠ DCE =∠AOB
三. 度量法
1、对“中”—角的顶点对量角器的中心
3、读数—读出角的另一边所对的度数
2、重合—角的一边与量角器的00刻度
线重合
B
C
A
F
E
D
700
∠ABC > ∠DEF
300
比较两个角的大小的方法有三种:
观察法
叠合法
度量法
小结:
角的分类
角 锐 角 直角 钝 角 平角 周角
范围
∠β
0°<∠β<90°
90°
90 °<∠β<180 ° 180° 360°
图示
┓
记一记
两个角的大小关系有三种,记作:
(1) ∠ABC > ∠DEF
(2)∠ABC< ∠DEF
(3)∠ABC = ∠DEF
A
D
(E)
(F)
C
B
D
(E)
(F)
A
A
B
C
(E)
(D)
(F)
B
C
估计图中∠1与∠2的大小关系,
1
2
2
1
(1)
(2)
练习:
并用适当的方法检验.
返回
下一张
上一张
退出
观察与思考
角的大小与角的两边画出的长短有关吗?
(1)角的大小与角的两边画出的
长短没有关系。
(2)角张开的程度越小,角度
就越小
结论:
迷人数学世界
用放大镜看蚂蚁,用放大镜看自己的手,用放大镜看精致的邮票,用放大镜从太阳光里取火等 等,都会得到令人开心的结果。那么,有没有放大镜放不大的事物呢?
你知道放大镜不能“放大”角
的度数的原因吗?
三. 角的和与差
B
C
A
700
F
E
D
300
因为∠ABC = 700 ,∠DEF=300,
所以∠ABC —∠DEF
=700—300
=400
所以∠ABC — ∠DEF
=∠ABD
⌒
2
⌒
1
∠2= ∠1+∠3
∠3= ∠2- ∠1
∠1= ∠2-∠3
三. 角的和差
3
⌒
观 察
如图,
O
A
B
C
∠AOC是 ∠AOB与 ∠BOC的和
∠AOB是∠AOC与∠BOC的差
记作:∠AOC= ∠AOB+ ∠BOC
记作:∠AOB=∠AOC—∠BOC
类似有∠BOC= ∠AOC—∠AOB
图中共有几个角?它们之间有什么关系?
D
O
B
C
A
练习2, 如图:
∠ AOC = ( ) + ( )
= ( ) - ( )
∠ BOC=( ) - ( )
= ( ) - ( )
∠ AOB
∠ BOC
∠ AOD
∠ COD
∠ COD
∠ BOD
∠ AOC
∠ AOB
如图∠ AOB= ∠ COD=900,
∠ AOD=1460, ∠ BOC= ;
340
D
练习3
A
B
C
D
E
1
2
⌒
⌒
图中∠1= ∠2, 试判断∠BAD和∠EAC的大小, 并说明理由.
冲击
解: ∠BAD= ∠2+ ∠DCA
∠EAC= ∠1+∠DCA
做一做
在纸上任意画一个角∠AOB,
把它对折,使角的两边OA与
OB重合,然后展开、铺平,
画出折痕OC。
则∠AOC与∠BOC有什么大小
关系?
A
O
B
C
角的平分线:从一个角的顶点引出的一条射线,
把这个角分成两个相等的角。
这条射线叫这个角的平分线。
如果给你任意一个角∠AOB,
你有什么方法画出它的平分线?
想一想
A
O
B
学一学
D
P
例2 如图 ∠ABC=90°,∠CBD=30°,
BP平分∠ABD。求∠ABP的度数。
A
B
C
探究:
借助一个三角尺可以画出哪些度数的角,用一副三角尺你还能画出哪些度数的角 上台来展示你的结果。
75°
15°
105 °
15°
120°
小结:
1、角的大小比较方法:
4、三角板可拼出哪些角?
3、角的和差计算
2、角的大小关系有哪些?
数一数:图中共有几个小于平角的角,找出规律。
O
A
B
C
D
O
B
C
A
(1)
(2)
1
2
3
O
A
B
C
D
E
F
O
A
B
C
D
E
(3)
(4)
……
如果以o为端点,有n条射线,那么组
成的角有多少个?
共有(n-1)+(n-2)+(n-3)+…+3+2+1=
n(n-1)/2
已知∠AOB=145°和∠AOC=25°
则∠BOC= 。
练一练
分类
思想
★★
练一练
2. 如图,OC是∠AOB的任意一条射线,
OD平分∠AOC,OE平分∠BOC。
问∠DOE与∠AOB有什么关系?
C
D
E
★★
A
B
O
3. 如图,∠AOB=64°,
OA1平分∠AOB,
OA2平分∠AOA1,
OA3平分∠AOA2,
OA4平分∠AOA3,
则∠AOA4= .
A
O
B
A1
A2
A3
A4
★★
练一练
如图所示的正方形网格中, ∠ 1 + ∠ 2 + ∠ 3+ ∠ 4+ ∠ 5+ ∠ 6+ ∠ 7= 。
1
2
3
4
5
6
7
试一试
作业:
课本144页10题
谢谢!!!!
