5.2运动的合成与分解—【新教材】人教版(2019)高中物理必修第二册课件
文档属性
| 名称 | 5.2运动的合成与分解—【新教材】人教版(2019)高中物理必修第二册课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 10.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-06 01:15:08 | ||
图片预览





文档简介
第五章 抛体运动
5.2 运动的合成与分解
若人在河中始终保持头朝正前方游向对岸,他会在什么位置靠岸?
教学目标
1.在具体情景中,知道合运动、分运动分别是什么,知道其同时性和独立性.
2.知道运动的合成与分解,理解运动的合成与分解遵循平行四边形定则.
3.会用作图和计算的方法,求解位移和速度的合成与分解问题.
下游。因为水也在流动。
新课导入
若人在河中始终保持头朝前方游向对岸,你认为他会在对岸的正前方达到,还是会偏向上游或下游?为什么?
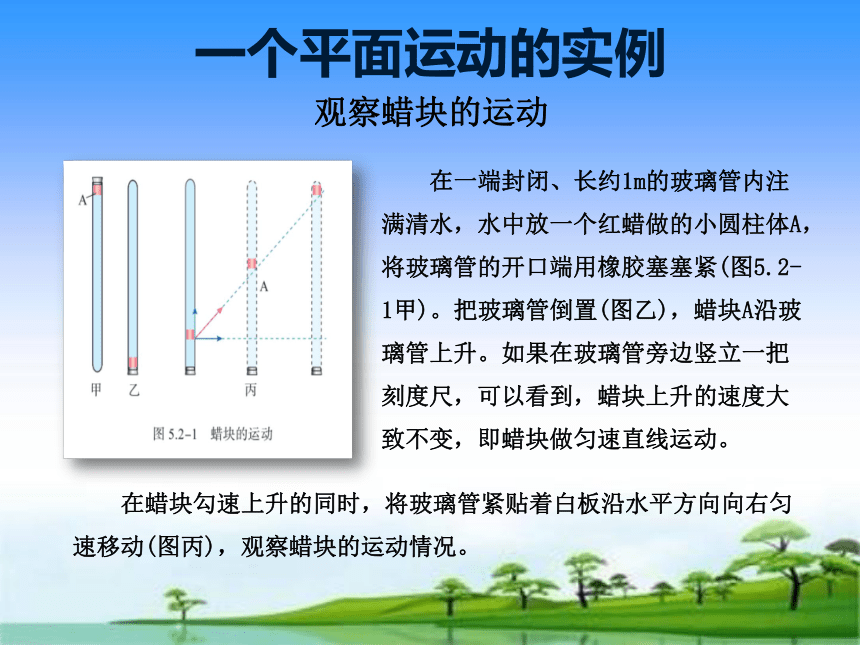
一个平面运动的实例
在一端封闭、长约1m的玻璃管内注满清水,水中放一个红蜡做的小圆柱体A,将玻璃管的开口端用橡胶塞塞紧(图5.2-1甲)。把玻璃管倒置(图乙),蜡块A沿玻璃管上升。如果在玻璃管旁边竖立一把刻度尺,可以看到,蜡块上升的速度大致不变,即蜡块做匀速直线运动。
观察蜡块的运动
在蜡块勾速上升的同时,将玻璃管紧贴着白板沿水平方向向右匀速移动(图丙),观察蜡块的运动情况。
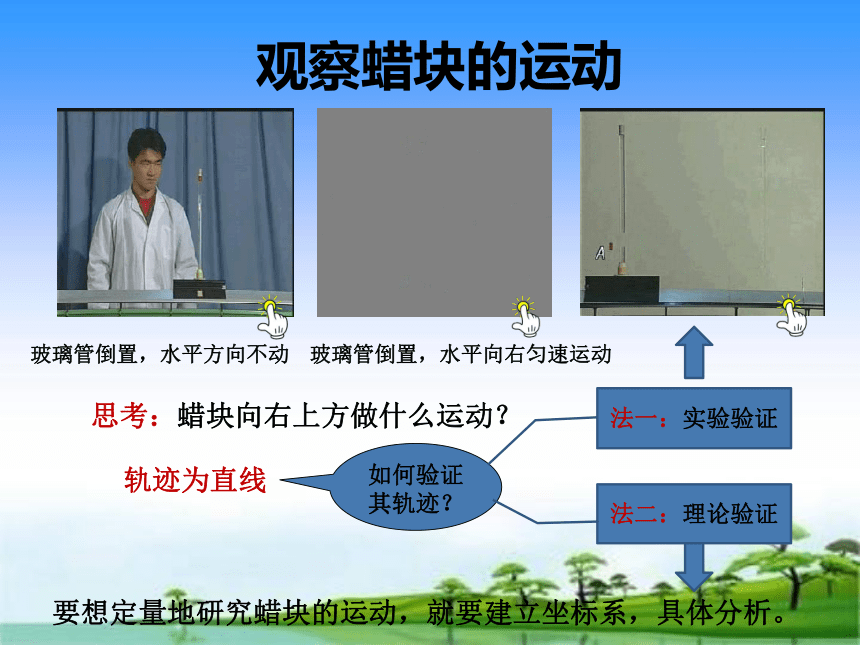
观察蜡块的运动
玻璃管倒置,水平方向不动
玻璃管倒置,水平向右匀速运动
思考:蜡块向右上方做什么运动?
轨迹为直线
要想定量地研究蜡块的运动,就要建立坐标系,具体分析。
如何验证其轨迹?
法一:实验验证
法二:理论验证
1、建立坐标系
以蜡块开始匀速运动的位置为原点O,以水平向右的方向和竖直向上的方向分别为x轴和y轴的方向,建立平面直角坐标系。
蜡块的位置P 的坐标:
x = vx t
y = vy t
理论分析蜡块的运动
蜡块的位置
v
vx
vy
O
P
2、蜡块运动的轨迹
x = vx t
y = vy t
在数学上,关于x、y两个变量的关系式可以 描述一条曲线(包括直线)。
y = —x
vx
vy
上面x、y的表达式中消去变量t,这样就得到:
由于vx和vy都是常量,所以 也是常量
—
vx
vy
代表的是一条过原点的直线,也就是说,蜡块的运动轨迹是直线。
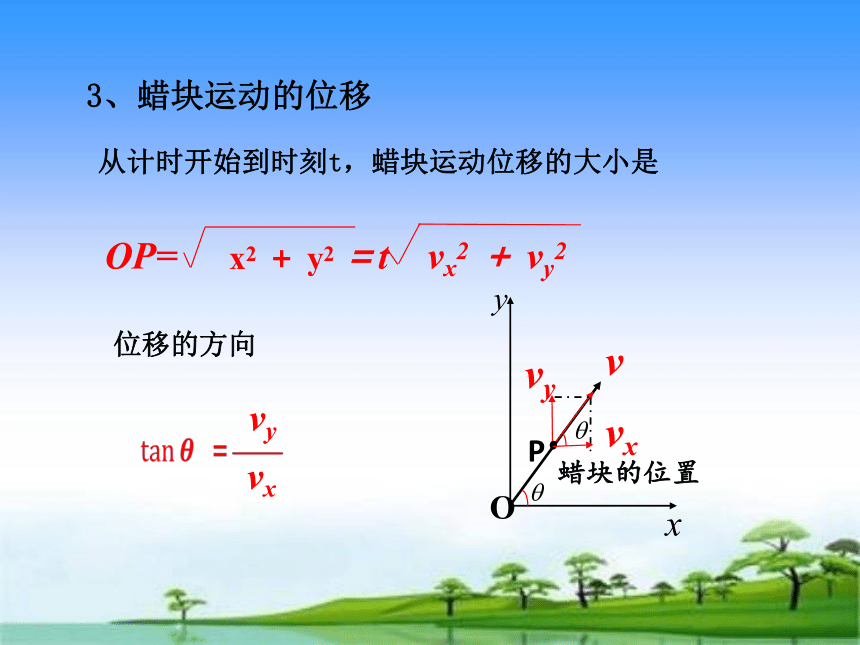
从计时开始到时刻t,蜡块运动位移的大小是
3、蜡块运动的位移
位移的方向
?
vx
vy
OP= =t vx2 + vy2
x2 + y2
蜡块的位置
v
vx
vy
O
P
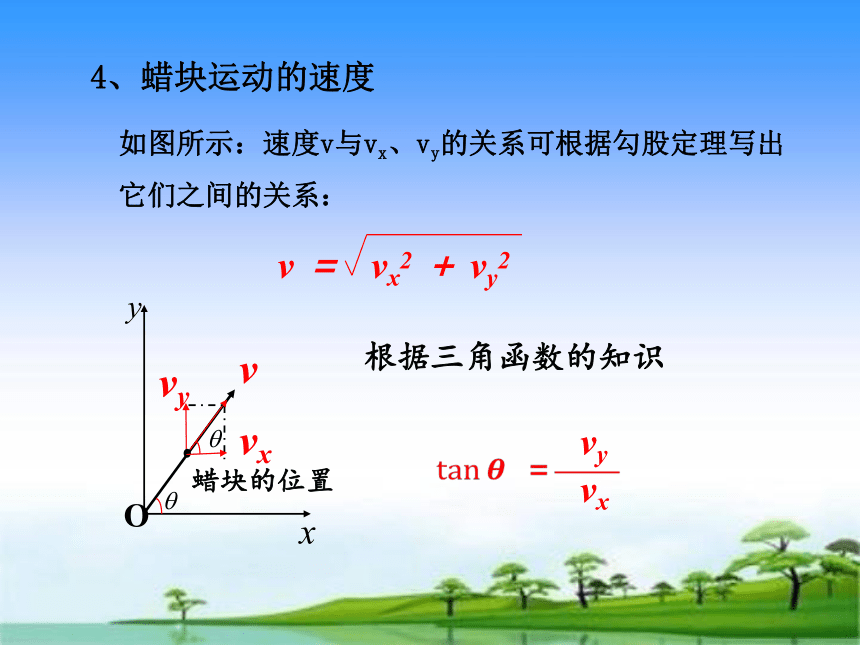
4、蜡块运动的速度
如图所示:速度v与vx、vy的关系可根据勾股定理写出它们之间的关系:
v = vx2 + vy2
?
vx
vy
根据三角函数的知识
蜡块的位置
v
vx
vy
O
1、合运动和分运动
(1)合运动:物体实际的运动叫合运动。
(2)分运动:物体同时参与合成运动的运动叫分运动。
如图:蜡块向右上方的运动可以看成由沿玻璃管向上的运动和水平向右的运动共同构成。蜡块相对于白板向右上方的运动叫作合运动。蜡块沿玻璃管向上的运动和它随着玻璃管向右的运动,都叫作分运动。
运动的合成与分解
2、合运动和分运动的特性
(1)独立性:一个物体同时参与几个分运动,各分运动独立进行,不受其他分运动的影响.
(2)等时性:各分运动经历的时间与合运动经历的时间相等,求物体的运动时间时,可选择一个简单的运动进行求解
(3)等效性:各分运动叠加起来与合运动有相同的效果,即分运动与合运动可以“等效替代"。
(4)同体性:各分运动与合运动是同一个物体的运动。
3、运动的合成与分解
(1)由分运动求合运动的过程叫运动的合成。
(2)由合运动求分运动的过程叫运动的分解。
(1)做曲线运动时,物体相对起始点的位移方向不断变化,在表示物体的位移时,尽量用它的位移在坐标轴方向的分量来表示,而位移分量可用该点的坐标表示.
(2)建立平面直角坐标系时,y轴正方向向下也是可以的,这时处于x轴下方的点的纵坐标不是负值而是正值.
4、曲线运动的合成与分解的注意事项
5、运动的合成与分解即为描述运动的物理量的合成与分解都遵守平行四边形定则。
位移合成与分解
速度合成与分解
加速度合成与分解
x
x2
x1
v
v2
v1
a
a2
a1
6、两个互成角度的直线运动的合运动性质的判断
合运动的性质取决于两个分运动的合初速度和合加速度(合外力)的关系
匀速
v1
匀速
v2
v
a1=0
a2=0
a=0
匀速
v1
匀加速
v2
v
a1=0
a2
(a)
v1=0匀加速
a
a1
a2
v=0
v2=0匀加速
匀速
v=0匀加速
v1
v2
v
a2
a1
a
匀加速
匀加速
匀加速
a2
a1
a
曲线
曲线
(1)两个匀速直线运动的合运动一定是匀速直线运动。
(2)两个初速度均为零的匀加速直线运动的合运动一定是匀加速直线运动
(3)一个匀速直线运动和一个匀变速直线运动的合运动是匀变速运动,当二者速度方向共线时为匀变速直线运动,不共线时为匀变速曲线运动。
(4)两个匀变速直线运动的合运动一定是匀变速运动,可能是直线运动,也可能是曲线运动。若两运动的合初速度方向与合加速度方向在同一条直线上,则合运动是匀变速直线运动,若两运动的合初速度方向与合加速度方向不在同一条直线上,则合运动是匀变速曲线运动。
例1:某商场设有步行楼梯和自动扶梯,步行楼梯每级的高度是0.15m,自动扶梯与水平面的夹角为30°,自动扶梯前进的速度是0.76m/s。有甲、乙两位顾客,分别从自动扶梯和步行楼梯的起点同时上楼,甲在自动扶梯上站立不动,乙在步行
楼梯上以每秒上两个台阶的
速度匀速上楼(如图所示)。
哪位顾客先到达楼上?如果
该楼层高4.56m,甲上楼用了
多少时间?
30°
v甲y
?
v甲
解:如图所示,甲在竖直方向的速度
V甲y=V甲sinθ=0.76×sin30°m/s=0.38m/S
乙在竖直方向的速度
V乙=2×0.15m/s=0.3m/s
因此V甲y > V乙,甲先到楼上。
t甲= = 12s
甲比乙先到达楼上,甲上楼用了12s。
分析:甲、乙两位顾客在竖直方向上的位移相等,可考虑比较他们在竖直方向的分速度。由竖直方向的位移和竖直方向的速度,可求出上楼所用的时间。
在“观察蜡块的运动”的实验中,如果将玻璃管紧贴着白板沿水平方向向右匀加速移动,若玻璃管内壁是光滑的,蜡块的轨迹还是一条直线吗?
不是直线,蜡块的轨迹将是一条曲线
思考与讨论
小船过河问题
小船
过河
分运动1:船随水漂流的运动
v水
分运动2:船相对于静水滑行的运动
v船
船的实际运动:
两个匀速直线运动的合运动
?
1.最短时间渡河
渡河时间取决于河的宽度d及船在垂直河岸方向上分速度的大小。若要渡河时间最短,只要使船头垂直于河岸航行即可,如图所示。这种情况下,小船一定在下游处靠岸。
d
v
v水
v船
?
最短时间:
渡河位移:
位移方向:
?
2.最小位移渡河
(1) v船>v水
d
当小船垂直河岸过河时,渡河位移最小,此时应将船头偏向上游。
v水
v船
?
渡河位移:
渡河时间:
船头与上游夹角:
?
?
2.最小位移渡河
(2) v船d
无论船头指向什么方向都无法使小船垂直渡河,即最小渡河位移不可能等于河宽d。
v水
v船
?
2.最小位移渡河
(3) v船d
以表示水流速度的有向线段的末端A为圆心,以船在静水中的速度大小为半径作圆,过O点作该圆的切线,与圆相切于B点,当v船与半径AB平行时,渡河位移最小。
v水
v船
A
O
B
v合
?
?
最短位移:
渡河时间:
船头与河岸夹角:
【例2】小船横渡200 m宽的河,水流速度为3 m/s,船在静水中的航速是5 m/s.
(1)当小船的船头始终正对对岸行驶时,它将经过多长时间在何处到达对岸?
(2)要使小船到达河的正对岸,应如何行驶?多长时间能到达对岸?(sin 37°=0.6)
答案:(1)40 s 在河的正对岸下游120 m处靠岸
(2)船头与河岸上游的夹角为53° 50 s
课堂小结
5.2 运动的合成与分解
若人在河中始终保持头朝正前方游向对岸,他会在什么位置靠岸?
教学目标
1.在具体情景中,知道合运动、分运动分别是什么,知道其同时性和独立性.
2.知道运动的合成与分解,理解运动的合成与分解遵循平行四边形定则.
3.会用作图和计算的方法,求解位移和速度的合成与分解问题.
下游。因为水也在流动。
新课导入
若人在河中始终保持头朝前方游向对岸,你认为他会在对岸的正前方达到,还是会偏向上游或下游?为什么?
一个平面运动的实例
在一端封闭、长约1m的玻璃管内注满清水,水中放一个红蜡做的小圆柱体A,将玻璃管的开口端用橡胶塞塞紧(图5.2-1甲)。把玻璃管倒置(图乙),蜡块A沿玻璃管上升。如果在玻璃管旁边竖立一把刻度尺,可以看到,蜡块上升的速度大致不变,即蜡块做匀速直线运动。
观察蜡块的运动
在蜡块勾速上升的同时,将玻璃管紧贴着白板沿水平方向向右匀速移动(图丙),观察蜡块的运动情况。
观察蜡块的运动
玻璃管倒置,水平方向不动
玻璃管倒置,水平向右匀速运动
思考:蜡块向右上方做什么运动?
轨迹为直线
要想定量地研究蜡块的运动,就要建立坐标系,具体分析。
如何验证其轨迹?
法一:实验验证
法二:理论验证
1、建立坐标系
以蜡块开始匀速运动的位置为原点O,以水平向右的方向和竖直向上的方向分别为x轴和y轴的方向,建立平面直角坐标系。
蜡块的位置P 的坐标:
x = vx t
y = vy t
理论分析蜡块的运动
蜡块的位置
v
vx
vy
O
P
2、蜡块运动的轨迹
x = vx t
y = vy t
在数学上,关于x、y两个变量的关系式可以 描述一条曲线(包括直线)。
y = —x
vx
vy
上面x、y的表达式中消去变量t,这样就得到:
由于vx和vy都是常量,所以 也是常量
—
vx
vy
代表的是一条过原点的直线,也就是说,蜡块的运动轨迹是直线。
从计时开始到时刻t,蜡块运动位移的大小是
3、蜡块运动的位移
位移的方向
?
vx
vy
OP= =t vx2 + vy2
x2 + y2
蜡块的位置
v
vx
vy
O
P
4、蜡块运动的速度
如图所示:速度v与vx、vy的关系可根据勾股定理写出它们之间的关系:
v = vx2 + vy2
?
vx
vy
根据三角函数的知识
蜡块的位置
v
vx
vy
O
1、合运动和分运动
(1)合运动:物体实际的运动叫合运动。
(2)分运动:物体同时参与合成运动的运动叫分运动。
如图:蜡块向右上方的运动可以看成由沿玻璃管向上的运动和水平向右的运动共同构成。蜡块相对于白板向右上方的运动叫作合运动。蜡块沿玻璃管向上的运动和它随着玻璃管向右的运动,都叫作分运动。
运动的合成与分解
2、合运动和分运动的特性
(1)独立性:一个物体同时参与几个分运动,各分运动独立进行,不受其他分运动的影响.
(2)等时性:各分运动经历的时间与合运动经历的时间相等,求物体的运动时间时,可选择一个简单的运动进行求解
(3)等效性:各分运动叠加起来与合运动有相同的效果,即分运动与合运动可以“等效替代"。
(4)同体性:各分运动与合运动是同一个物体的运动。
3、运动的合成与分解
(1)由分运动求合运动的过程叫运动的合成。
(2)由合运动求分运动的过程叫运动的分解。
(1)做曲线运动时,物体相对起始点的位移方向不断变化,在表示物体的位移时,尽量用它的位移在坐标轴方向的分量来表示,而位移分量可用该点的坐标表示.
(2)建立平面直角坐标系时,y轴正方向向下也是可以的,这时处于x轴下方的点的纵坐标不是负值而是正值.
4、曲线运动的合成与分解的注意事项
5、运动的合成与分解即为描述运动的物理量的合成与分解都遵守平行四边形定则。
位移合成与分解
速度合成与分解
加速度合成与分解
x
x2
x1
v
v2
v1
a
a2
a1
6、两个互成角度的直线运动的合运动性质的判断
合运动的性质取决于两个分运动的合初速度和合加速度(合外力)的关系
匀速
v1
匀速
v2
v
a1=0
a2=0
a=0
匀速
v1
匀加速
v2
v
a1=0
a2
(a)
v1=0匀加速
a
a1
a2
v=0
v2=0匀加速
匀速
v=0匀加速
v1
v2
v
a2
a1
a
匀加速
匀加速
匀加速
a2
a1
a
曲线
曲线
(1)两个匀速直线运动的合运动一定是匀速直线运动。
(2)两个初速度均为零的匀加速直线运动的合运动一定是匀加速直线运动
(3)一个匀速直线运动和一个匀变速直线运动的合运动是匀变速运动,当二者速度方向共线时为匀变速直线运动,不共线时为匀变速曲线运动。
(4)两个匀变速直线运动的合运动一定是匀变速运动,可能是直线运动,也可能是曲线运动。若两运动的合初速度方向与合加速度方向在同一条直线上,则合运动是匀变速直线运动,若两运动的合初速度方向与合加速度方向不在同一条直线上,则合运动是匀变速曲线运动。
例1:某商场设有步行楼梯和自动扶梯,步行楼梯每级的高度是0.15m,自动扶梯与水平面的夹角为30°,自动扶梯前进的速度是0.76m/s。有甲、乙两位顾客,分别从自动扶梯和步行楼梯的起点同时上楼,甲在自动扶梯上站立不动,乙在步行
楼梯上以每秒上两个台阶的
速度匀速上楼(如图所示)。
哪位顾客先到达楼上?如果
该楼层高4.56m,甲上楼用了
多少时间?
30°
v甲y
?
v甲
解:如图所示,甲在竖直方向的速度
V甲y=V甲sinθ=0.76×sin30°m/s=0.38m/S
乙在竖直方向的速度
V乙=2×0.15m/s=0.3m/s
因此V甲y > V乙,甲先到楼上。
t甲= = 12s
甲比乙先到达楼上,甲上楼用了12s。
分析:甲、乙两位顾客在竖直方向上的位移相等,可考虑比较他们在竖直方向的分速度。由竖直方向的位移和竖直方向的速度,可求出上楼所用的时间。
在“观察蜡块的运动”的实验中,如果将玻璃管紧贴着白板沿水平方向向右匀加速移动,若玻璃管内壁是光滑的,蜡块的轨迹还是一条直线吗?
不是直线,蜡块的轨迹将是一条曲线
思考与讨论
小船过河问题
小船
过河
分运动1:船随水漂流的运动
v水
分运动2:船相对于静水滑行的运动
v船
船的实际运动:
两个匀速直线运动的合运动
?
1.最短时间渡河
渡河时间取决于河的宽度d及船在垂直河岸方向上分速度的大小。若要渡河时间最短,只要使船头垂直于河岸航行即可,如图所示。这种情况下,小船一定在下游处靠岸。
d
v
v水
v船
?
最短时间:
渡河位移:
位移方向:
?
2.最小位移渡河
(1) v船>v水
d
当小船垂直河岸过河时,渡河位移最小,此时应将船头偏向上游。
v水
v船
?
渡河位移:
渡河时间:
船头与上游夹角:
?
?
2.最小位移渡河
(2) v船
无论船头指向什么方向都无法使小船垂直渡河,即最小渡河位移不可能等于河宽d。
v水
v船
?
2.最小位移渡河
(3) v船
以表示水流速度的有向线段的末端A为圆心,以船在静水中的速度大小为半径作圆,过O点作该圆的切线,与圆相切于B点,当v船与半径AB平行时,渡河位移最小。
v水
v船
A
O
B
v合
?
?
最短位移:
渡河时间:
船头与河岸夹角:
【例2】小船横渡200 m宽的河,水流速度为3 m/s,船在静水中的航速是5 m/s.
(1)当小船的船头始终正对对岸行驶时,它将经过多长时间在何处到达对岸?
(2)要使小船到达河的正对岸,应如何行驶?多长时间能到达对岸?(sin 37°=0.6)
答案:(1)40 s 在河的正对岸下游120 m处靠岸
(2)船头与河岸上游的夹角为53° 50 s
课堂小结
