5.2 运动的合成和分解(第一课时)—【新教材】人教版(2019)高中物理必修二课件
文档属性
| 名称 | 5.2 运动的合成和分解(第一课时)—【新教材】人教版(2019)高中物理必修二课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 23.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-06 05:55:06 | ||
图片预览





文档简介
人教版 必修 第二册
5.2运动的合成和分解
(第一课时)
问题
思考:若船在河中始终保持船头朝正前方驶向对岸,你认为船会在对岸的正前方到达,还是会偏向上游或下游?生活中类似的运动如何研究?
阅读P6演示实验
蜡块在平面内的运动
观察蜡块的运动
实验一:玻璃管倒置,水平方向不动
蜡块向上匀速运动
实验二:玻璃管倒置,水平向右匀速运动
(1)水平方向:
(2)竖直方向:
(3)以后面白纸为背景:
蜡块随管向右做匀速直线运动。
蜡块沿管向上做匀速直线运动。
蜡块相对白纸是向右上方运动的。
蜡块在平面内的运动
观察蜡块的运动
思考:蜡块向右上方做什么运动?
猜想:蜡块沿右上方运动轨迹如何?
轨迹为直线
如何验证其轨迹?
法一:实验验证
法二:理论验证
蜡块在平面内的运动
思考:如何验证轨迹为直线?
蜡块运动轨迹满足y=kx即可(定量研究蜡块运动)
要想定量地研究蜡块的运动,就要建立坐标系,具体分析。
如何建立作标
阅读P7建立坐标系内容回答
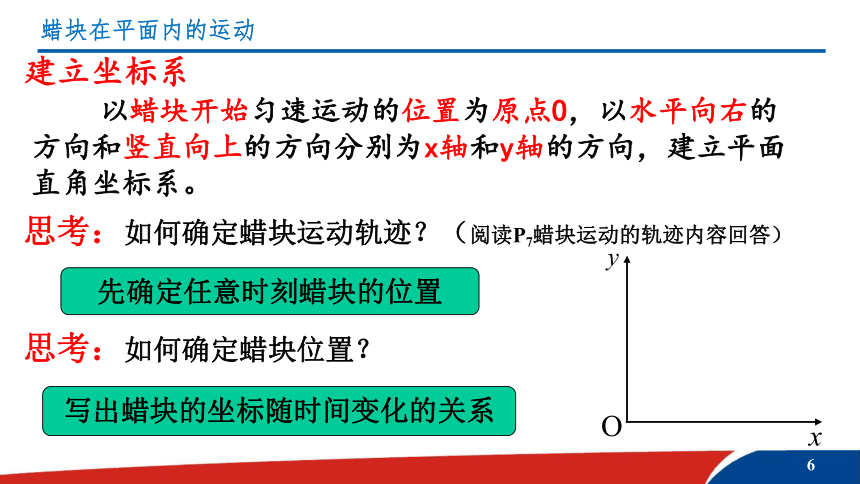
建立坐标系
以蜡块开始匀速运动的位置为原点O,以水平向右的方向和竖直向上的方向分别为x轴和y轴的方向,建立平面直角坐标系。
O
蜡块在平面内的运动
思考:如何确定蜡块运动轨迹?(阅读P7蜡块运动的轨迹内容回答)
先确定任意时刻蜡块的位置
思考:如何确定蜡块位置?
写出蜡块的坐标随时间变化的关系
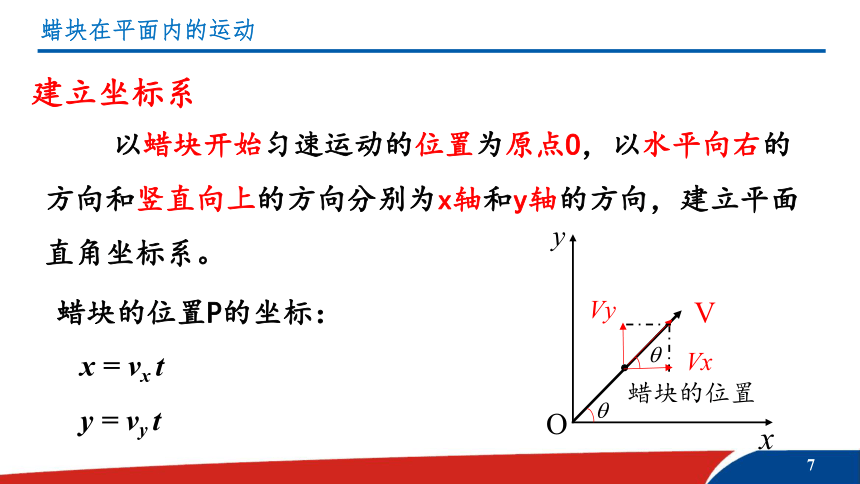
建立坐标系
以蜡块开始匀速运动的位置为原点O,以水平向右的方向和竖直向上的方向分别为x轴和y轴的方向,建立平面直角坐标系。
蜡块的位置
V
Vy
Vx
O
蜡块的位置P的坐标:
x = vx t
y = vy t
蜡块在平面内的运动
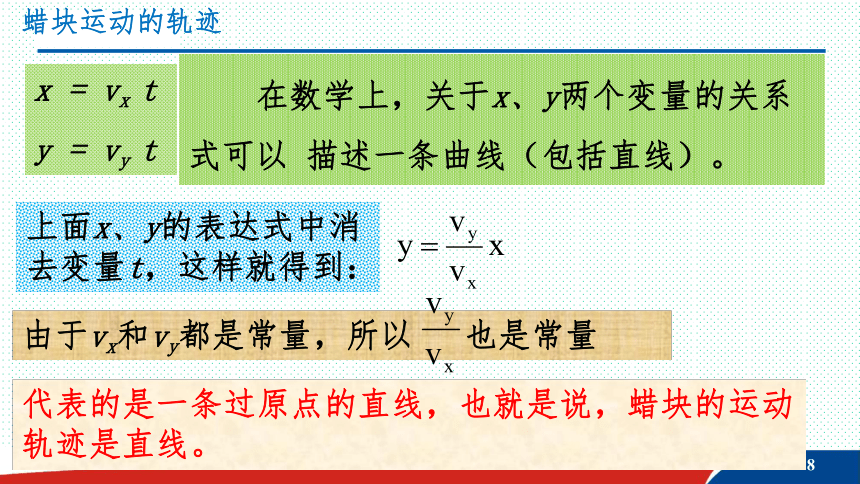
蜡块运动的轨迹
x = vx t
y = vy t
在数学上,关于x、y两个变量的关系式可以 描述一条曲线(包括直线)。
上面x、y的表达式中消去变量t,这样就得到:
由于vx和vy都是常量,所以 也是常量
代表的是一条过原点的直线,也就是说,蜡块的运动轨迹是直线。
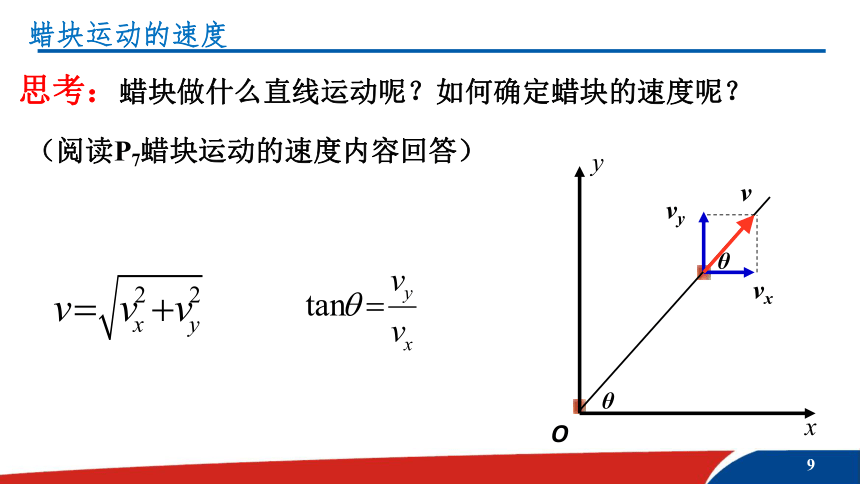
蜡块运动的速度
O
x
y
vx
vy
v
θ
θ
思考:蜡块做什么直线运动呢?如何确定蜡块的速度呢?
(阅读P7蜡块运动的速度内容回答)
我们看到蜡块向右上方的运动可以看成由沿玻璃管向上的运动和水平向右的运动共同构成。蜡块沿玻璃管向上的运动和它随着玻璃管向右的运动,都叫作分运动;而蜡块相对于白纸向右上方的运动叫作合运动。
由分运动求合运动的过程,叫作运动的合成;
由合运动求分运动的过程,叫作运动的分解。
运动的合成与分解
合运动与分运动
在物理学中,如果一个物体实际发生的运动产生的效果跟另外两个运动产生的效果相同,我们就把物体的实际运动叫做这两个运动的合运动,这两个运动叫做这一实际运动的分运动
物体的实际运动的位移、速度、加速度分别叫合位移、合速度、合加速度。
运动的合成与分解即为描述运动的物理量的合成与分解 都遵守平行四边形定则。
位移合成与分解
速度合成与分解
加速度合成与分解
x
x2
x1
v
v2
v1
a
a2
a1
y
合运动
竖直分运动
水平分运动
合运动与分运动的关系
1)等效性:合运动的效果与各分运动共同产生的效果相同。
2)等时性:合运动与分运动所用时间相同。
3)独立性:各分运动各自按自己的规律运动,互不干扰。
合运动与分运动的区分原则:物体实际进行的运动一定是合运动,对应于平行四边形的对角线.
蜡块运动的位移
O
x
y
vx
vy
v
θ
θ
思考:如何求解蜡块的位移呢?
P
物体在一平面直角坐标系内运动,开始时位于坐标原点,物体在x轴和y轴方向运动的速度一时间图像分别如图甲、乙所示。求:(1)t1=2s时物体的速度大小;
(2)前4s内物体的位移大小。
【例】
【例】
某商场设有步行楼梯和自动扶梯,步行楼梯每级的高度是0.15m,自动扶梯与水平面的夹角为30°,自动扶梯前进的速度是0.76m/s。有甲、乙两位顾客,分别从自动扶梯和步行楼梯的起点同时上楼,甲在自动扶梯上站立不动,乙在步行楼梯上以每秒上两个台阶的速度匀速上楼(如图所示)。哪位顾客先到达楼上?如果该楼层高4.56m,甲上楼用了多少时间?
解:如图所示,甲在竖直方向的速度
v甲y=v甲sinθ=0.76×sin30°m/s=0.38m/s
乙在竖直方向的速度
因此v甲y >v乙,甲先到楼上。
甲比乙先到达楼上,甲上楼用了12s。
30°
v甲y
?
v甲
两个直线运动的合运动的运动轨迹可不可能是曲线?
为什么会做曲线运动呢?如何判断?
思考:如何判断是直线运动还是曲线运动?(判断轨迹)
合力F合的方向或加速度a的方向与合速度v合的方向是否同一直线
两个直线运动的合运动的分析
分析思路
先把速度合成
再把加速度合成
然后再看加速度与速度是否在同一条直线上
直线运动
在同一条直线上
不在在同一条直线上
曲线运动
1.两个匀速直线运动的合运动
两个直线运动的合运动的分析
v1
v2
竖直向上做匀速直线运动
水平向右做匀速直线运动
把速度平移到同一起点
v1
v2
v
匀速直线运动
a=0
2.一个匀速直线运动一个匀加速直线运动的合运动
两个直线运动的合运动的分析
v1
v2
水平向右做匀速直线运动
把速度平移到同一起点
v1
v2
v
匀变速直线运动
(1)两速度在同一条直线上
水平向右做匀加速直线运动
a2
=a
加速度与速度在同一条直线上
a2
2.一个匀速直线运动一个匀加速直线运动的合运动
两个直线运动的合运动的分析
v1
v2
把速度平移到同一起点
v1
v2
v
匀变速曲线运动
(2)两速度不在同一条直线上
水平向右做匀加速直线运动
a2
=a
加速度与速度不在同一条直线上
竖直向上做匀速直线运动
a2
两个直线运动的合运动的分析
v1
v2
水平向右做匀加速直线运动
把速度平移到同一起点
v1
v2
v
匀变速直线运动
(1)两速度在同一条直线上
水平向右做匀加速直线运动
a2
a
加速度与速度在同一条直线上
3.两个初匀速均不为零的匀加速直线运动的合运动
a1
a1
a2
3.两个初匀速均不为零的匀加速直线运动的合运动
两个直线运动的合运动的分析
v1
v2
把速度平移到同一起点
v1
v2
v
匀变速直线线运动
(2)两速度不在同一条直线上
水平向右做匀加速直线运动
a2
a
思考:加速度与速度在同一条直线上需满足什么条件?
竖直向上做匀加速直线运动
a1
a1
a2
3.两个初匀速均不为零的匀加速直线运动的合运动
两个直线运动的合运动的分析
v1
v2
把速度平移到同一起点
v1
v2
v
匀变速曲线线运动
(2)两速度不在同一条直线上
水平向右做匀加速直线运动
a2
a
竖直向上做匀加速直线运动
a1
a1
a2
加速度与速度不在同一条直线上
关于两个运动的合运动,下列说法中正确的是( )
A.两个直线运动的合运动一定是直线运动
B.两个互成角度的匀速直线运动的合运动一定是匀速直线运动
C.两个互成角度的匀变速直线运动的合运动一定是匀变速直线运动
D.两个分运动的时间和它们的合运动的时间不相等
B
课堂练习
问题
思考:若船在河中始终保持船头朝正前方驶向对岸,你认为船会在对岸的正前方到达,还是会偏向上游或下游?生活中类似的运动如何研究?
5.2运动的合成和分解
(第一课时)
问题
思考:若船在河中始终保持船头朝正前方驶向对岸,你认为船会在对岸的正前方到达,还是会偏向上游或下游?生活中类似的运动如何研究?
阅读P6演示实验
蜡块在平面内的运动
观察蜡块的运动
实验一:玻璃管倒置,水平方向不动
蜡块向上匀速运动
实验二:玻璃管倒置,水平向右匀速运动
(1)水平方向:
(2)竖直方向:
(3)以后面白纸为背景:
蜡块随管向右做匀速直线运动。
蜡块沿管向上做匀速直线运动。
蜡块相对白纸是向右上方运动的。
蜡块在平面内的运动
观察蜡块的运动
思考:蜡块向右上方做什么运动?
猜想:蜡块沿右上方运动轨迹如何?
轨迹为直线
如何验证其轨迹?
法一:实验验证
法二:理论验证
蜡块在平面内的运动
思考:如何验证轨迹为直线?
蜡块运动轨迹满足y=kx即可(定量研究蜡块运动)
要想定量地研究蜡块的运动,就要建立坐标系,具体分析。
如何建立作标
阅读P7建立坐标系内容回答
建立坐标系
以蜡块开始匀速运动的位置为原点O,以水平向右的方向和竖直向上的方向分别为x轴和y轴的方向,建立平面直角坐标系。
O
蜡块在平面内的运动
思考:如何确定蜡块运动轨迹?(阅读P7蜡块运动的轨迹内容回答)
先确定任意时刻蜡块的位置
思考:如何确定蜡块位置?
写出蜡块的坐标随时间变化的关系
建立坐标系
以蜡块开始匀速运动的位置为原点O,以水平向右的方向和竖直向上的方向分别为x轴和y轴的方向,建立平面直角坐标系。
蜡块的位置
V
Vy
Vx
O
蜡块的位置P的坐标:
x = vx t
y = vy t
蜡块在平面内的运动
蜡块运动的轨迹
x = vx t
y = vy t
在数学上,关于x、y两个变量的关系式可以 描述一条曲线(包括直线)。
上面x、y的表达式中消去变量t,这样就得到:
由于vx和vy都是常量,所以 也是常量
代表的是一条过原点的直线,也就是说,蜡块的运动轨迹是直线。
蜡块运动的速度
O
x
y
vx
vy
v
θ
θ
思考:蜡块做什么直线运动呢?如何确定蜡块的速度呢?
(阅读P7蜡块运动的速度内容回答)
我们看到蜡块向右上方的运动可以看成由沿玻璃管向上的运动和水平向右的运动共同构成。蜡块沿玻璃管向上的运动和它随着玻璃管向右的运动,都叫作分运动;而蜡块相对于白纸向右上方的运动叫作合运动。
由分运动求合运动的过程,叫作运动的合成;
由合运动求分运动的过程,叫作运动的分解。
运动的合成与分解
合运动与分运动
在物理学中,如果一个物体实际发生的运动产生的效果跟另外两个运动产生的效果相同,我们就把物体的实际运动叫做这两个运动的合运动,这两个运动叫做这一实际运动的分运动
物体的实际运动的位移、速度、加速度分别叫合位移、合速度、合加速度。
运动的合成与分解即为描述运动的物理量的合成与分解 都遵守平行四边形定则。
位移合成与分解
速度合成与分解
加速度合成与分解
x
x2
x1
v
v2
v1
a
a2
a1
y
合运动
竖直分运动
水平分运动
合运动与分运动的关系
1)等效性:合运动的效果与各分运动共同产生的效果相同。
2)等时性:合运动与分运动所用时间相同。
3)独立性:各分运动各自按自己的规律运动,互不干扰。
合运动与分运动的区分原则:物体实际进行的运动一定是合运动,对应于平行四边形的对角线.
蜡块运动的位移
O
x
y
vx
vy
v
θ
θ
思考:如何求解蜡块的位移呢?
P
物体在一平面直角坐标系内运动,开始时位于坐标原点,物体在x轴和y轴方向运动的速度一时间图像分别如图甲、乙所示。求:(1)t1=2s时物体的速度大小;
(2)前4s内物体的位移大小。
【例】
【例】
某商场设有步行楼梯和自动扶梯,步行楼梯每级的高度是0.15m,自动扶梯与水平面的夹角为30°,自动扶梯前进的速度是0.76m/s。有甲、乙两位顾客,分别从自动扶梯和步行楼梯的起点同时上楼,甲在自动扶梯上站立不动,乙在步行楼梯上以每秒上两个台阶的速度匀速上楼(如图所示)。哪位顾客先到达楼上?如果该楼层高4.56m,甲上楼用了多少时间?
解:如图所示,甲在竖直方向的速度
v甲y=v甲sinθ=0.76×sin30°m/s=0.38m/s
乙在竖直方向的速度
因此v甲y >v乙,甲先到楼上。
甲比乙先到达楼上,甲上楼用了12s。
30°
v甲y
?
v甲
两个直线运动的合运动的运动轨迹可不可能是曲线?
为什么会做曲线运动呢?如何判断?
思考:如何判断是直线运动还是曲线运动?(判断轨迹)
合力F合的方向或加速度a的方向与合速度v合的方向是否同一直线
两个直线运动的合运动的分析
分析思路
先把速度合成
再把加速度合成
然后再看加速度与速度是否在同一条直线上
直线运动
在同一条直线上
不在在同一条直线上
曲线运动
1.两个匀速直线运动的合运动
两个直线运动的合运动的分析
v1
v2
竖直向上做匀速直线运动
水平向右做匀速直线运动
把速度平移到同一起点
v1
v2
v
匀速直线运动
a=0
2.一个匀速直线运动一个匀加速直线运动的合运动
两个直线运动的合运动的分析
v1
v2
水平向右做匀速直线运动
把速度平移到同一起点
v1
v2
v
匀变速直线运动
(1)两速度在同一条直线上
水平向右做匀加速直线运动
a2
=a
加速度与速度在同一条直线上
a2
2.一个匀速直线运动一个匀加速直线运动的合运动
两个直线运动的合运动的分析
v1
v2
把速度平移到同一起点
v1
v2
v
匀变速曲线运动
(2)两速度不在同一条直线上
水平向右做匀加速直线运动
a2
=a
加速度与速度不在同一条直线上
竖直向上做匀速直线运动
a2
两个直线运动的合运动的分析
v1
v2
水平向右做匀加速直线运动
把速度平移到同一起点
v1
v2
v
匀变速直线运动
(1)两速度在同一条直线上
水平向右做匀加速直线运动
a2
a
加速度与速度在同一条直线上
3.两个初匀速均不为零的匀加速直线运动的合运动
a1
a1
a2
3.两个初匀速均不为零的匀加速直线运动的合运动
两个直线运动的合运动的分析
v1
v2
把速度平移到同一起点
v1
v2
v
匀变速直线线运动
(2)两速度不在同一条直线上
水平向右做匀加速直线运动
a2
a
思考:加速度与速度在同一条直线上需满足什么条件?
竖直向上做匀加速直线运动
a1
a1
a2
3.两个初匀速均不为零的匀加速直线运动的合运动
两个直线运动的合运动的分析
v1
v2
把速度平移到同一起点
v1
v2
v
匀变速曲线线运动
(2)两速度不在同一条直线上
水平向右做匀加速直线运动
a2
a
竖直向上做匀加速直线运动
a1
a1
a2
加速度与速度不在同一条直线上
关于两个运动的合运动,下列说法中正确的是( )
A.两个直线运动的合运动一定是直线运动
B.两个互成角度的匀速直线运动的合运动一定是匀速直线运动
C.两个互成角度的匀变速直线运动的合运动一定是匀变速直线运动
D.两个分运动的时间和它们的合运动的时间不相等
B
课堂练习
问题
思考:若船在河中始终保持船头朝正前方驶向对岸,你认为船会在对岸的正前方到达,还是会偏向上游或下游?生活中类似的运动如何研究?
