5.4 抛体运动的规律—【新教材】人教版(2019)高中物理必修二课件
文档属性
| 名称 | 5.4 抛体运动的规律—【新教材】人教版(2019)高中物理必修二课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-06 06:05:24 | ||
图片预览








文档简介
5.4 抛体运动的规律
平抛运动:
水平方向为匀速直线运动
竖直方向为自由落体运动
一、速度
α
vx
vy
v
O
x
y
v0
P (x,y)
时间为t时,物体运动到点P处
h
【例题 1】将一个物体以 10 m/s 的速度从 10 m 的高度水平抛出,落地时它的速度方向与水平地面的夹角θ是多少?
不计空气阻力,g 取 10 m/s2 。
二、位移
l
O
x
y
P (x,y)
B
A
v0
时间为t时,物体运动到点P处
抛物线
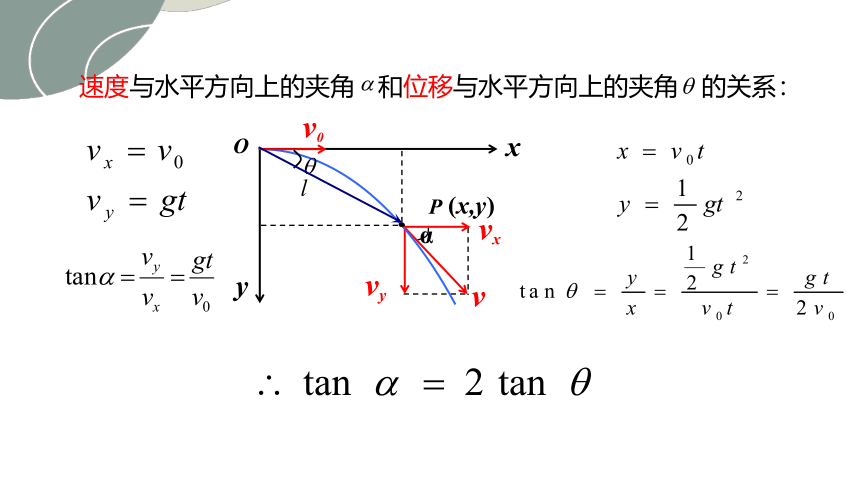
速度与水平方向上的夹角 和位移与水平方向上的夹角 的关系:
α
vx
vy
v
O
x
y
v0
P (x,y)
【例题2】 如图 5.4-3,某同学利用无人机玩“投弹”游戏。无 人机以 v0 = 2 m/s 的速度水平向右匀速飞行,在某时 刻释放了一个小球。此时无人机到水平地面的距离 h = 20 m,空气阻力忽略不计,g 取 10 m/s2 。
(1)求小球下落的时间。
(2)求小球释放点与落地点之间的水平距离。
解:(1)以小球从无人机释放时的位置为原点O建立平面直
角坐标系, x 轴沿初速度方向,y轴竖直向下。
设小球的落地点为P,下落的时间为t,则满足
所以小球落地的时间
(2)因此,小球落地点与释放点之间的水平距离
小球落地的时间为2s,落地点与释放点之间的水平距离为4m
如图所示,以v0的水平初速度抛出的物体,飞行一段时间后,垂直撞在倾角为θ的斜面上。求物体飞行的时间(g取10m/s2)
v0
30o
如图所示,在倾角为θ的斜面上以初速度v0 水平抛出一物体,物体刚好落在斜面上的B点,求物体飞行的时间。
θ
v0
B
A
平抛运动的几个结论
平抛运动的几个结论
1.如图所示,滑板运动员以速度v0从距离地面高度为h的平台末端水平飞出,落在水平地面上.运动员和滑板均可视为质点,忽略空气阻力的影响.下列说法中正确的是( )
A.h一定时,v0越大,运动员在空中运动时间越长
B.h一定时,v0越大,运动员落地瞬间速度越大
C.运动员落地瞬间速度与高度h无关
D.运动员落地位置与v0大小无关
B
根据 知,运动员在空中运动的时间由高度决定,与初速度无关,故A错误;落地时竖直分速度 ,则运动员落地的速度 ,即高度一定时,初速度越大,落地瞬间速度越大,故B正确;运动员落地时速度方向与水平方向夹角的正切值 ,可知落地瞬间速度大小和方向均与高度有关,故C错误;水平位移由初速度和高度共同决定,则运动员落地的位置与初速度有关,故D错误.
2.(多选)平抛物体的初速度为v0,当水平方向分位移与竖直方向分位移相等时,下列说法正确的是( )
A.运动的时间t=2v0/g
B.瞬时速率vt= v0
C.水平分速度与竖直分速度大小相等
D.位移大小等于
ABD
3.如图所示,一架在2 000 m高空中以200 m/s的速度水平匀速飞行的轰炸机,要想用两枚炸弹分别炸山脚和山顶的目标A和B.已知山高为720 m,山脚与山顶的水平距离为1 000 m,若不计空气阻力,g取10 m/s2,则投弹的时间间隔应为( )
A.4 s B.5 s
C.9 s D.16 s
C
第一颗炸弹的飞行时间t1=20 s,轰炸机投第一颗炸弹时离山脚的水平距离x1=vt1=4 000 m.第二颗炸弹的飞行时间t2=16 s,飞行的水平距离x2=vt2=3 200 m,则投弹的时间间隔t=9 s,故选C.
4.如图所示,水平房顶高H=5 m,墙高h=3.2 m,墙到房子的距离l=3 m,墙外马路宽d=10 m.欲使小球从房顶水平飞出落在墙外的马路上,求小球离开房顶时的速度v0应满足的条件.(墙的厚度不计,g取10 m/s2)
如图甲所示,设球刚好触墙而过时小球离开房顶的速度为v1,则小球自房顶飞出后做平抛运动到达墙头时,水平位移大小为l,竖直位移大小为(H-h),则y=H-h=(5-3.2) m=1.8 m,
由 得小球自飞出后运动到墙头所用的时间为
由l=v1t1得小球离开房顶时的速度为
设小球飞出后恰好落在墙外的马路边缘时离开房顶的速度为v2,如图乙所示,此过程水平位移大小为
(l+d),竖直位移大小为H,则小球在空中的飞行时间t2满足 ,则 ,
由l+d=v2t2得 ,
即小球恰好落在马路边缘时从房顶飞出的速度大小为13 m/s.
综上分析知,欲使小球离开房顶后能落在马路上,则小球离开房顶时的速度v0应满足v1≤v0≤v2,即
5 m/s≤v0≤13 m/s.
平抛运动:
水平方向为匀速直线运动
竖直方向为自由落体运动
一、速度
α
vx
vy
v
O
x
y
v0
P (x,y)
时间为t时,物体运动到点P处
h
【例题 1】将一个物体以 10 m/s 的速度从 10 m 的高度水平抛出,落地时它的速度方向与水平地面的夹角θ是多少?
不计空气阻力,g 取 10 m/s2 。
二、位移
l
O
x
y
P (x,y)
B
A
v0
时间为t时,物体运动到点P处
抛物线
速度与水平方向上的夹角 和位移与水平方向上的夹角 的关系:
α
vx
vy
v
O
x
y
v0
P (x,y)
【例题2】 如图 5.4-3,某同学利用无人机玩“投弹”游戏。无 人机以 v0 = 2 m/s 的速度水平向右匀速飞行,在某时 刻释放了一个小球。此时无人机到水平地面的距离 h = 20 m,空气阻力忽略不计,g 取 10 m/s2 。
(1)求小球下落的时间。
(2)求小球释放点与落地点之间的水平距离。
解:(1)以小球从无人机释放时的位置为原点O建立平面直
角坐标系, x 轴沿初速度方向,y轴竖直向下。
设小球的落地点为P,下落的时间为t,则满足
所以小球落地的时间
(2)因此,小球落地点与释放点之间的水平距离
小球落地的时间为2s,落地点与释放点之间的水平距离为4m
如图所示,以v0的水平初速度抛出的物体,飞行一段时间后,垂直撞在倾角为θ的斜面上。求物体飞行的时间(g取10m/s2)
v0
30o
如图所示,在倾角为θ的斜面上以初速度v0 水平抛出一物体,物体刚好落在斜面上的B点,求物体飞行的时间。
θ
v0
B
A
平抛运动的几个结论
平抛运动的几个结论
1.如图所示,滑板运动员以速度v0从距离地面高度为h的平台末端水平飞出,落在水平地面上.运动员和滑板均可视为质点,忽略空气阻力的影响.下列说法中正确的是( )
A.h一定时,v0越大,运动员在空中运动时间越长
B.h一定时,v0越大,运动员落地瞬间速度越大
C.运动员落地瞬间速度与高度h无关
D.运动员落地位置与v0大小无关
B
根据 知,运动员在空中运动的时间由高度决定,与初速度无关,故A错误;落地时竖直分速度 ,则运动员落地的速度 ,即高度一定时,初速度越大,落地瞬间速度越大,故B正确;运动员落地时速度方向与水平方向夹角的正切值 ,可知落地瞬间速度大小和方向均与高度有关,故C错误;水平位移由初速度和高度共同决定,则运动员落地的位置与初速度有关,故D错误.
2.(多选)平抛物体的初速度为v0,当水平方向分位移与竖直方向分位移相等时,下列说法正确的是( )
A.运动的时间t=2v0/g
B.瞬时速率vt= v0
C.水平分速度与竖直分速度大小相等
D.位移大小等于
ABD
3.如图所示,一架在2 000 m高空中以200 m/s的速度水平匀速飞行的轰炸机,要想用两枚炸弹分别炸山脚和山顶的目标A和B.已知山高为720 m,山脚与山顶的水平距离为1 000 m,若不计空气阻力,g取10 m/s2,则投弹的时间间隔应为( )
A.4 s B.5 s
C.9 s D.16 s
C
第一颗炸弹的飞行时间t1=20 s,轰炸机投第一颗炸弹时离山脚的水平距离x1=vt1=4 000 m.第二颗炸弹的飞行时间t2=16 s,飞行的水平距离x2=vt2=3 200 m,则投弹的时间间隔t=9 s,故选C.
4.如图所示,水平房顶高H=5 m,墙高h=3.2 m,墙到房子的距离l=3 m,墙外马路宽d=10 m.欲使小球从房顶水平飞出落在墙外的马路上,求小球离开房顶时的速度v0应满足的条件.(墙的厚度不计,g取10 m/s2)
如图甲所示,设球刚好触墙而过时小球离开房顶的速度为v1,则小球自房顶飞出后做平抛运动到达墙头时,水平位移大小为l,竖直位移大小为(H-h),则y=H-h=(5-3.2) m=1.8 m,
由 得小球自飞出后运动到墙头所用的时间为
由l=v1t1得小球离开房顶时的速度为
设小球飞出后恰好落在墙外的马路边缘时离开房顶的速度为v2,如图乙所示,此过程水平位移大小为
(l+d),竖直位移大小为H,则小球在空中的飞行时间t2满足 ,则 ,
由l+d=v2t2得 ,
即小球恰好落在马路边缘时从房顶飞出的速度大小为13 m/s.
综上分析知,欲使小球离开房顶后能落在马路上,则小球离开房顶时的速度v0应满足v1≤v0≤v2,即
5 m/s≤v0≤13 m/s.
