2020-2021学年人教版 九年级数学下册 27.1 图形的相似 同步练习(Word版 含解析)
文档属性
| 名称 | 2020-2021学年人教版 九年级数学下册 27.1 图形的相似 同步练习(Word版 含解析) | 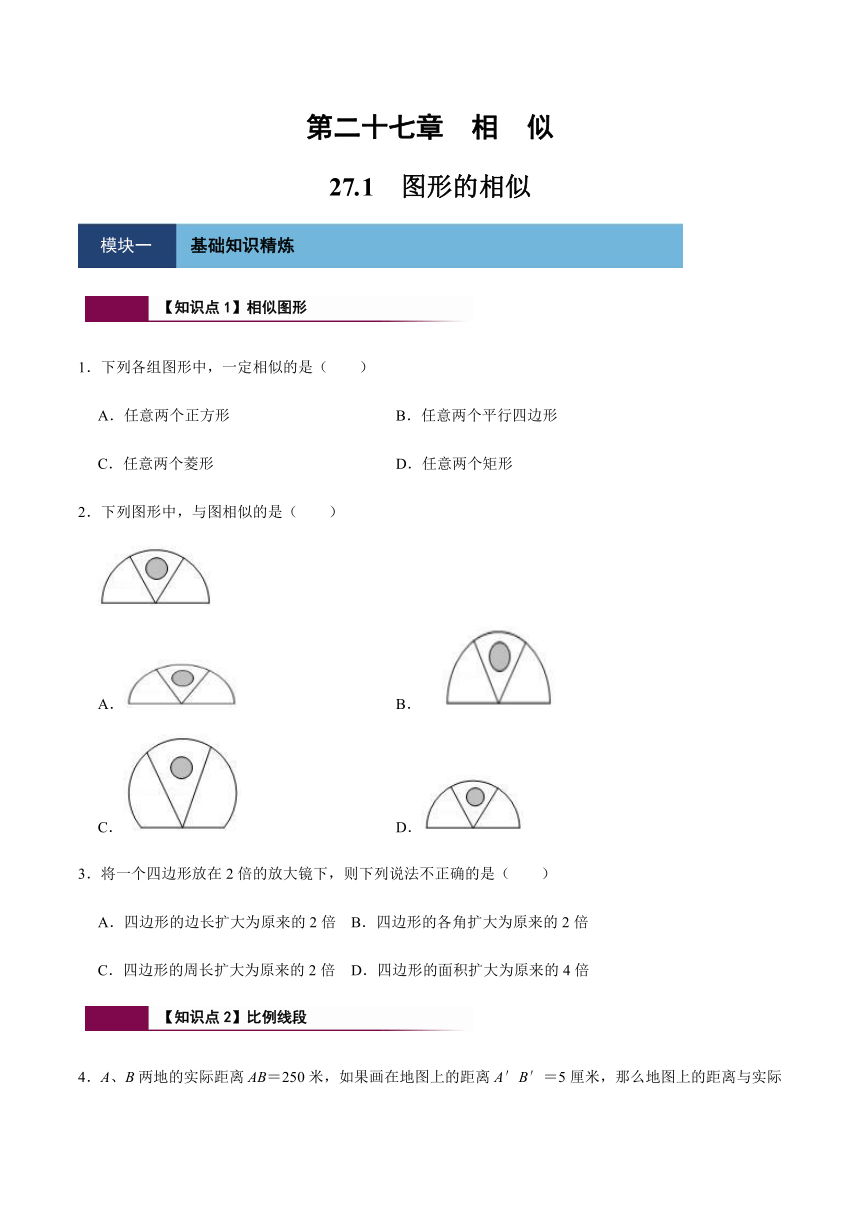 | |
| 格式 | docx | ||
| 文件大小 | 165.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-06 06:06:41 | ||
图片预览




文档简介
第二十七章 相 似
27.1 图形的相似
基础知识精炼
模块一
基础知识精炼
模块一
【知识点1】相似图形
【知识点1】相似图形
1.下列各组图形中,一定相似的是( )
A.任意两个正方形 B.任意两个平行四边形
C.任意两个菱形 D.任意两个矩形
2.下列图形中,与图相似的是( )
A. B.
C. D.
3.将一个四边形放在2倍的放大镜下,则下列说法不正确的是( )
A.四边形的边长扩大为原来的2倍 B.四边形的各角扩大为原来的2倍
C.四边形的周长扩大为原来的2倍 D.四边形的面积扩大为原来的4倍
【知识点2】比例线段
【知识点2】比例线段
4.A、B两地的实际距离AB=250米,如果画在地图上的距离A′B′=5厘米,那么地图上的距离与实际距离的比为( )
A.1:500 B.1:5000 C.500:1 D.5000:1
5.如果C是线段AB延长线上一点,且AC:BC=3:1,那么AB:BC等于( )
A.2:1 B.1:2 C.4:1 D.1:4
6.以下四组线段,成比例的是( )
A.1,2,3,4 B.2,3,4,5 C.3,4,6,8 D.5,6,7,8
7.已知a,d,b,c依次成比例线段,其中a=3cm,b=4cm,c=6cm,则d= cm.
8.若a2=b3=c4,且2a+b+c=33,则a﹣b+c= .
【知识点3】相似多边形与性质
【知识点3】相似多边形与性质
9.两个相似多边形的一组对应边分别是3cm和4.5cm,如果它们的周长之和是80cm,那么较大的多边形的周长是( )
A.16cm B.32cm C.48cm D.52cm
10.两个相似多边形的相似比为4:9,那么它们的周长比为( )
A.2:3 B.4:9 C.2:3 D.16:81
11.如图,四边形ABCD与四边形EFGH相似,则下列角的度数正确的是( )
A.∠D=81° B.∠F=83° C.∠G=78° D.∠H=76°
12.如图,E、F分别为矩形ABCD的边AD,BC的中点.若矩形ABCD与矩形EABF相似,AB=6,则AD的长为 .
综合能力提升
模块二
综合能力提升
模块二
13.下列结论中,错误的有:( )
①所有的菱形都相似;
②放大镜下的图形与原图形不一定相似;
③等边三角形都相似;
④有一个角为110度的两个等腰三角形相似;
⑤所有的矩形不一定相似.
A.1个 B.2个 C.3个 D.4个
14.如果x+32=y-13=z-24,且x+y+z=18,则2x﹣y﹣z的值为( )
A.5 B.﹣15 C.10 D.15
15.已知四条线段a,b,c,d满足ab=cd,则下列等式一定成立的是( )
A.ad=cd B.a+cb+d=ab
C.a2b=c2b D.2a+c2d+b=ab
16.若一个多边形的各边长分别为2,3,4,5,6,另一个和它相似的多边形的最长边长为24,则另一个多边形的最短边长为( )
A.6 B.8 C.10 D.12
17.已知x2=y3=z5,且x+2y+3z=﹣46,求x,y,z的值.
18.如图,四边形ABCD与四边形A'B'C'D'相似的图形,点A与点A′、点B与点B′、点C与点C′、点D与点D′分别是对应顶点,已知数据如图所示,求未知边x、y的长度和角α、β的大小.
19.在AB=20m,AD=30m的矩形花坛四周修筑小路.
(1)如果四周的小路的宽均相等,都是x,如图1,那么小路四周所围成的矩形A1B1C1D1和矩形ABCD相似吗?请说明理由;
(2)如果相对着的两条小路的宽均相等,宽度分别为x、y,如图2,试问小路的宽x与y的比值为多少时,能使得小路四周所围成的矩形A1B1C1D1和矩形ABCD相似?请说明理由.
参考答案与试题解析
1.解:A、任意两个正方形的对应角相等,对应边的比也相等,故一定相似,符合题意;
B、任意两个平行四边形对应边的比不一定相等,对应角也不一定相等,故不一定相似,不符合题意;
C、任意两个菱形的对应边的比相等,但对应角不一定相等,故不一定相似,不符合题意;
D、任意两个矩形对应角相等,但对应边的比不一定相等,故不一定相似,不符合题意,
故选:A.
2.解:观察图形知该图象于D相似,故D符合,
故选:D.
3.解:放大前后的多边形按照比例放大与缩小,因此它们是相似多边形,放大后的倍数就是相似比,
∴选项:A,C,D正确,
故选:B.
4.解:取米作为共同的长度单位,那么AB=250米,A'B'=5厘米=0.05米,
所以A′B′AB=0.05250=15000,
所以地图上的距离与实际距离的比为1:5000.
故选:B.
5.解:∵AC:BC=3:1,
∴设AC=3x,则BC=x,AB=2x,
则AB:BC=2:1.
故选:A.
6.解:A、1:2≠3:4,则不是成比例线段,选项不符合题意;
B、2:3≠4:5,则不是成比例线段,选项不符合题意;
C、3:6=4:8,则是成比例线段,选项符合题意;
D、5:6≠7:8,则是成比例线段,选项不符合题意.
故选:C.
7.解:∵a,d,b,c依次成比例线段,
∴a:d=b:c,
∴d=acb,
∵a=3cm,b=4cm,c=6cm,
∴d=3×64=4.5cm.
故答案为:4.5.
8.解:设a2=b3=c4=k(k≠0),则a=2k,b=3k,c=4k,
∵2a+b+c=33,
∴4k+3k+4k=33,
∴k=3,
∴a﹣b+c=2k﹣3k+4k=3k=3×3=9;
故答案为:9.
9.解:设较大多边形与较小多边形的周长分别是m,n.则nm=34.5=23.
因而n=23m.
根据面积之和是80cm2.得到m+23m=80.
解得:m=48cm.
故选:C.
10.解:∵两个相似多边形的相似比为4:9,
∴两个相似多边形周长的比等于4:9,
故选:B.
11.解:∵四边形ABCD和四边形EFGH相似,
∴∠B=∠F=78°,∠A=∠E=118°,∠C=∠G=88°,
∴∠D=360°﹣78°﹣118°﹣88°=76°.
故选:D.
12.解:∵矩形ABCD与矩形EABF相似,
∴AEAB=ABAD,即12AD6=6AD,
解得,AD=62,
故答案为:62.
13.解:①:菱形的两组对角不一定分别对应相等,故所有的菱形不一定都相似;即:选项①错误.
②:放大镜下的图形与原图形只是大小不相等,但形状相同,所以它们一定相似;即:选项②错误.
③:等边三角形的三个内角相等,三条边都相等,故所有的等边三角形都相似;即:选项③正确
④:有一个角为110度的两个等腰三角形一定相似.因为它们的顶角均为110°,两锐角均为35°,根据“两内角对应相等的两个三角形相似”即可判定.故:选项④正确.
⑤:只有长与宽对应成比例的两个矩形相似,故选项⑤正确
故选:B.
14.解:设x+32=y-13=z-24=k,则x=2k﹣3,y=3k+1,z=4k+2,
∵x+y+z=18,
∴2k﹣3+3k+1+4k+2=18,
∴k=2,
∴x=1,y=7,z=10,
∴2x﹣y﹣z=2﹣7﹣10=﹣15;
故选:B.
15.解:A、由已知ab=cd得ad=bc,故选项不符合题意;
B、根据分式的合比性质,等式一定成立,故选项符合题意;
C、根据分式的性质可知该等式不成立,故选项不符合题意;
D、根据分式的合比性质,等式不一定成立,故选项不符合题意.
故选:B.
16.解:设这个多边形的最短边长为x,
∵两个多边形相似,
∴246=x2,
解得,x=8,
故选:B.
17.解:设x=2k,y=3k,z=5k,(k≠0),
∵x+2y+3z=﹣46,
∴2k+6k+15k=﹣46,
解得:k=﹣2,
∴x=﹣4,y=﹣6,z=﹣10.
18.解:在四边形ABCD中,∠D=∠D'=β=55°,
∠A=α=360°﹣55°﹣90°﹣60°=155°,
∵四边形ABCD∽四边形A'B'C'D',
∴9x=128=y10,
∴x=6,y=15.
19.(1)解:(1)如果四周的小路的宽均相等,那么小路四周所围成的矩形A′B′C′D′和矩形ABCD不相似;
设四周的小路的宽为x,
∵30+2x30=15+x15,20+2x20=10+x10,
∴30+2x30≠20+2x20,
∴小路四周所围成的矩形A′B′C′D′和矩形ABCD不相似;
(2)∵当30+2y30=20+2x20时,小路四周所围成的矩形A′B′C′D′和矩形ABCD相似,
解得:xy=23,
∴路的宽x与y的比值为2:3时,能使小路四周所围成的矩形A′B′C′D′和矩形ABCD相似.
27.1 图形的相似
基础知识精炼
模块一
基础知识精炼
模块一
【知识点1】相似图形
【知识点1】相似图形
1.下列各组图形中,一定相似的是( )
A.任意两个正方形 B.任意两个平行四边形
C.任意两个菱形 D.任意两个矩形
2.下列图形中,与图相似的是( )
A. B.
C. D.
3.将一个四边形放在2倍的放大镜下,则下列说法不正确的是( )
A.四边形的边长扩大为原来的2倍 B.四边形的各角扩大为原来的2倍
C.四边形的周长扩大为原来的2倍 D.四边形的面积扩大为原来的4倍
【知识点2】比例线段
【知识点2】比例线段
4.A、B两地的实际距离AB=250米,如果画在地图上的距离A′B′=5厘米,那么地图上的距离与实际距离的比为( )
A.1:500 B.1:5000 C.500:1 D.5000:1
5.如果C是线段AB延长线上一点,且AC:BC=3:1,那么AB:BC等于( )
A.2:1 B.1:2 C.4:1 D.1:4
6.以下四组线段,成比例的是( )
A.1,2,3,4 B.2,3,4,5 C.3,4,6,8 D.5,6,7,8
7.已知a,d,b,c依次成比例线段,其中a=3cm,b=4cm,c=6cm,则d= cm.
8.若a2=b3=c4,且2a+b+c=33,则a﹣b+c= .
【知识点3】相似多边形与性质
【知识点3】相似多边形与性质
9.两个相似多边形的一组对应边分别是3cm和4.5cm,如果它们的周长之和是80cm,那么较大的多边形的周长是( )
A.16cm B.32cm C.48cm D.52cm
10.两个相似多边形的相似比为4:9,那么它们的周长比为( )
A.2:3 B.4:9 C.2:3 D.16:81
11.如图,四边形ABCD与四边形EFGH相似,则下列角的度数正确的是( )
A.∠D=81° B.∠F=83° C.∠G=78° D.∠H=76°
12.如图,E、F分别为矩形ABCD的边AD,BC的中点.若矩形ABCD与矩形EABF相似,AB=6,则AD的长为 .
综合能力提升
模块二
综合能力提升
模块二
13.下列结论中,错误的有:( )
①所有的菱形都相似;
②放大镜下的图形与原图形不一定相似;
③等边三角形都相似;
④有一个角为110度的两个等腰三角形相似;
⑤所有的矩形不一定相似.
A.1个 B.2个 C.3个 D.4个
14.如果x+32=y-13=z-24,且x+y+z=18,则2x﹣y﹣z的值为( )
A.5 B.﹣15 C.10 D.15
15.已知四条线段a,b,c,d满足ab=cd,则下列等式一定成立的是( )
A.ad=cd B.a+cb+d=ab
C.a2b=c2b D.2a+c2d+b=ab
16.若一个多边形的各边长分别为2,3,4,5,6,另一个和它相似的多边形的最长边长为24,则另一个多边形的最短边长为( )
A.6 B.8 C.10 D.12
17.已知x2=y3=z5,且x+2y+3z=﹣46,求x,y,z的值.
18.如图,四边形ABCD与四边形A'B'C'D'相似的图形,点A与点A′、点B与点B′、点C与点C′、点D与点D′分别是对应顶点,已知数据如图所示,求未知边x、y的长度和角α、β的大小.
19.在AB=20m,AD=30m的矩形花坛四周修筑小路.
(1)如果四周的小路的宽均相等,都是x,如图1,那么小路四周所围成的矩形A1B1C1D1和矩形ABCD相似吗?请说明理由;
(2)如果相对着的两条小路的宽均相等,宽度分别为x、y,如图2,试问小路的宽x与y的比值为多少时,能使得小路四周所围成的矩形A1B1C1D1和矩形ABCD相似?请说明理由.
参考答案与试题解析
1.解:A、任意两个正方形的对应角相等,对应边的比也相等,故一定相似,符合题意;
B、任意两个平行四边形对应边的比不一定相等,对应角也不一定相等,故不一定相似,不符合题意;
C、任意两个菱形的对应边的比相等,但对应角不一定相等,故不一定相似,不符合题意;
D、任意两个矩形对应角相等,但对应边的比不一定相等,故不一定相似,不符合题意,
故选:A.
2.解:观察图形知该图象于D相似,故D符合,
故选:D.
3.解:放大前后的多边形按照比例放大与缩小,因此它们是相似多边形,放大后的倍数就是相似比,
∴选项:A,C,D正确,
故选:B.
4.解:取米作为共同的长度单位,那么AB=250米,A'B'=5厘米=0.05米,
所以A′B′AB=0.05250=15000,
所以地图上的距离与实际距离的比为1:5000.
故选:B.
5.解:∵AC:BC=3:1,
∴设AC=3x,则BC=x,AB=2x,
则AB:BC=2:1.
故选:A.
6.解:A、1:2≠3:4,则不是成比例线段,选项不符合题意;
B、2:3≠4:5,则不是成比例线段,选项不符合题意;
C、3:6=4:8,则是成比例线段,选项符合题意;
D、5:6≠7:8,则是成比例线段,选项不符合题意.
故选:C.
7.解:∵a,d,b,c依次成比例线段,
∴a:d=b:c,
∴d=acb,
∵a=3cm,b=4cm,c=6cm,
∴d=3×64=4.5cm.
故答案为:4.5.
8.解:设a2=b3=c4=k(k≠0),则a=2k,b=3k,c=4k,
∵2a+b+c=33,
∴4k+3k+4k=33,
∴k=3,
∴a﹣b+c=2k﹣3k+4k=3k=3×3=9;
故答案为:9.
9.解:设较大多边形与较小多边形的周长分别是m,n.则nm=34.5=23.
因而n=23m.
根据面积之和是80cm2.得到m+23m=80.
解得:m=48cm.
故选:C.
10.解:∵两个相似多边形的相似比为4:9,
∴两个相似多边形周长的比等于4:9,
故选:B.
11.解:∵四边形ABCD和四边形EFGH相似,
∴∠B=∠F=78°,∠A=∠E=118°,∠C=∠G=88°,
∴∠D=360°﹣78°﹣118°﹣88°=76°.
故选:D.
12.解:∵矩形ABCD与矩形EABF相似,
∴AEAB=ABAD,即12AD6=6AD,
解得,AD=62,
故答案为:62.
13.解:①:菱形的两组对角不一定分别对应相等,故所有的菱形不一定都相似;即:选项①错误.
②:放大镜下的图形与原图形只是大小不相等,但形状相同,所以它们一定相似;即:选项②错误.
③:等边三角形的三个内角相等,三条边都相等,故所有的等边三角形都相似;即:选项③正确
④:有一个角为110度的两个等腰三角形一定相似.因为它们的顶角均为110°,两锐角均为35°,根据“两内角对应相等的两个三角形相似”即可判定.故:选项④正确.
⑤:只有长与宽对应成比例的两个矩形相似,故选项⑤正确
故选:B.
14.解:设x+32=y-13=z-24=k,则x=2k﹣3,y=3k+1,z=4k+2,
∵x+y+z=18,
∴2k﹣3+3k+1+4k+2=18,
∴k=2,
∴x=1,y=7,z=10,
∴2x﹣y﹣z=2﹣7﹣10=﹣15;
故选:B.
15.解:A、由已知ab=cd得ad=bc,故选项不符合题意;
B、根据分式的合比性质,等式一定成立,故选项符合题意;
C、根据分式的性质可知该等式不成立,故选项不符合题意;
D、根据分式的合比性质,等式不一定成立,故选项不符合题意.
故选:B.
16.解:设这个多边形的最短边长为x,
∵两个多边形相似,
∴246=x2,
解得,x=8,
故选:B.
17.解:设x=2k,y=3k,z=5k,(k≠0),
∵x+2y+3z=﹣46,
∴2k+6k+15k=﹣46,
解得:k=﹣2,
∴x=﹣4,y=﹣6,z=﹣10.
18.解:在四边形ABCD中,∠D=∠D'=β=55°,
∠A=α=360°﹣55°﹣90°﹣60°=155°,
∵四边形ABCD∽四边形A'B'C'D',
∴9x=128=y10,
∴x=6,y=15.
19.(1)解:(1)如果四周的小路的宽均相等,那么小路四周所围成的矩形A′B′C′D′和矩形ABCD不相似;
设四周的小路的宽为x,
∵30+2x30=15+x15,20+2x20=10+x10,
∴30+2x30≠20+2x20,
∴小路四周所围成的矩形A′B′C′D′和矩形ABCD不相似;
(2)∵当30+2y30=20+2x20时,小路四周所围成的矩形A′B′C′D′和矩形ABCD相似,
解得:xy=23,
∴路的宽x与y的比值为2:3时,能使小路四周所围成的矩形A′B′C′D′和矩形ABCD相似.
