2020-2021学年人教版 九年级数学下册 27.2.1 平行线分线段成比例 同步练习(Word版 含解析)
文档属性
| 名称 | 2020-2021学年人教版 九年级数学下册 27.2.1 平行线分线段成比例 同步练习(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 284.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-06 06:21:51 | ||
图片预览

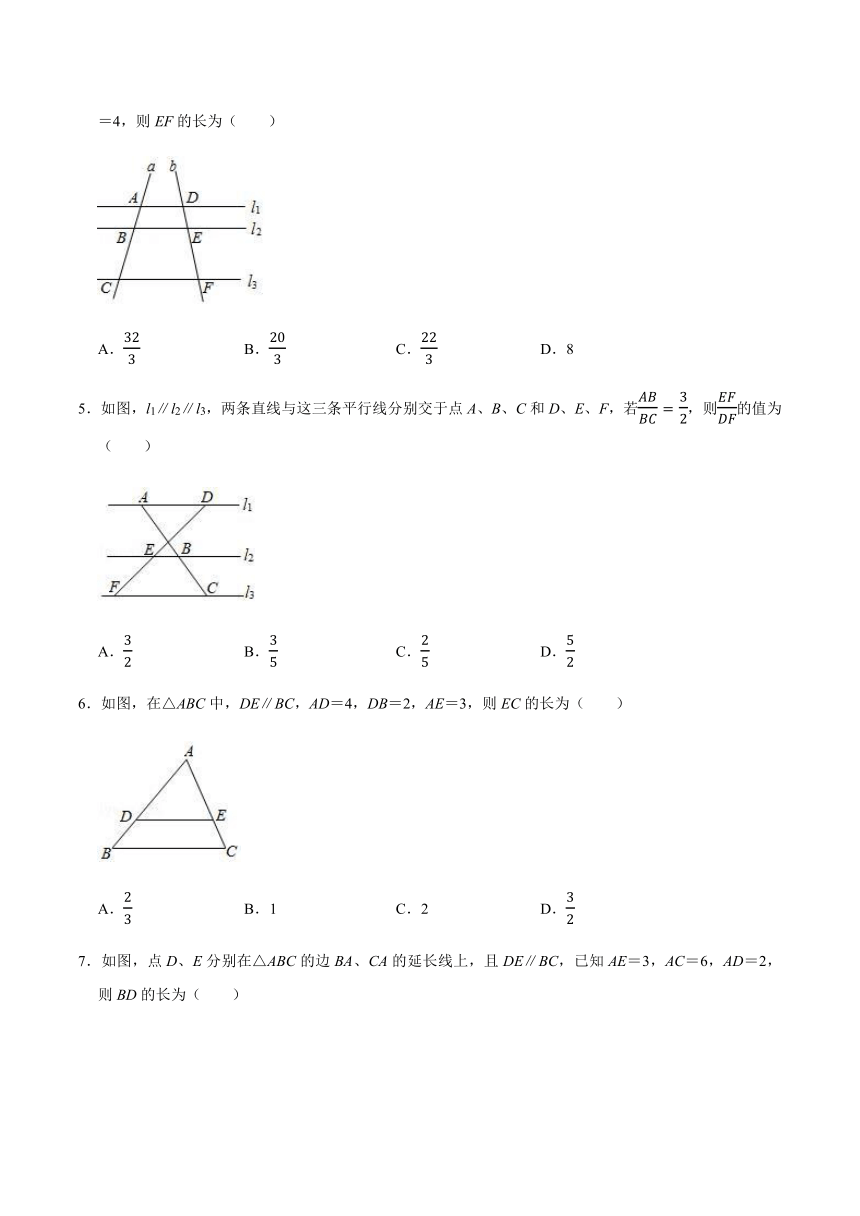

文档简介
106680001212850027.2 相似三角形
27.2.1 相似三角形的判定
第1课时 平行线分线段成比例
基础知识精炼
模块一
基础知识精炼
模块一
【知识点1】相似三角形及其相似比
【知识点1】相似三角形及其相似比
1.若△ABC∽△DEF,相似比为1:2,AB=4,则DE的长为( )
A.2 B.4 C.6 D.8
2.如图,若△ABC∽△DEF,则∠D的度数为( )
A.30° B.50° C.100° D.以上都不对
3.如图,△ABO∽△CDO,若BO=8,DO=4,CD=3,则AB的长是( )
A.2 B.3 C.4 D.6
【知识点2】平行线分线段成比例及其推论
【知识点2】平行线分线段成比例及其推论
4.如图,l1∥l2∥l3,直线a,b分别与l1,l2,l3相交于点A,B,C和点D,E,F,若AB=3,BC=5,DE=4,则EF的长为( )
A.323 B.203 C.223 D.8
5.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F,若ABBC=32,则EFDF的值为( )
A.32 B.35 C.25 D.52
6.如图,在△ABC中,DE∥BC,AD=4,DB=2,AE=3,则EC的长为( )
A.23 B.1 C.2 D.32
7.如图,点D、E分别在△ABC的边BA、CA的延长线上,且DE∥BC,已知AE=3,AC=6,AD=2,则BD的长为( )
A.4 B.6 C.7 D.8
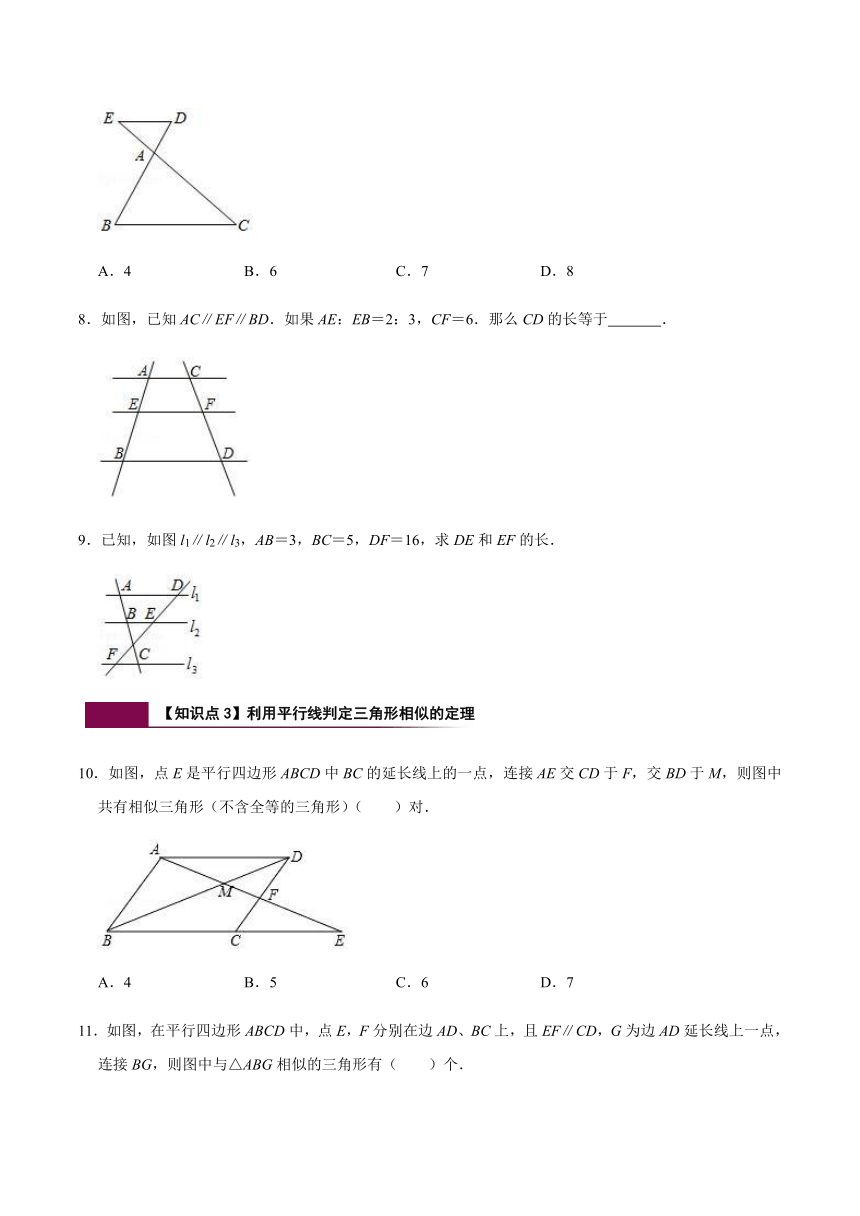
8.如图,已知AC∥EF∥BD.如果AE:EB=2:3,CF=6.那么CD的长等于 .
9.已知,如图l1∥l2∥l3,AB=3,BC=5,DF=16,求DE和EF的长.
【知识点3】利用平行线判定三角形相似的定理
【知识点3】利用平行线判定三角形相似的定理
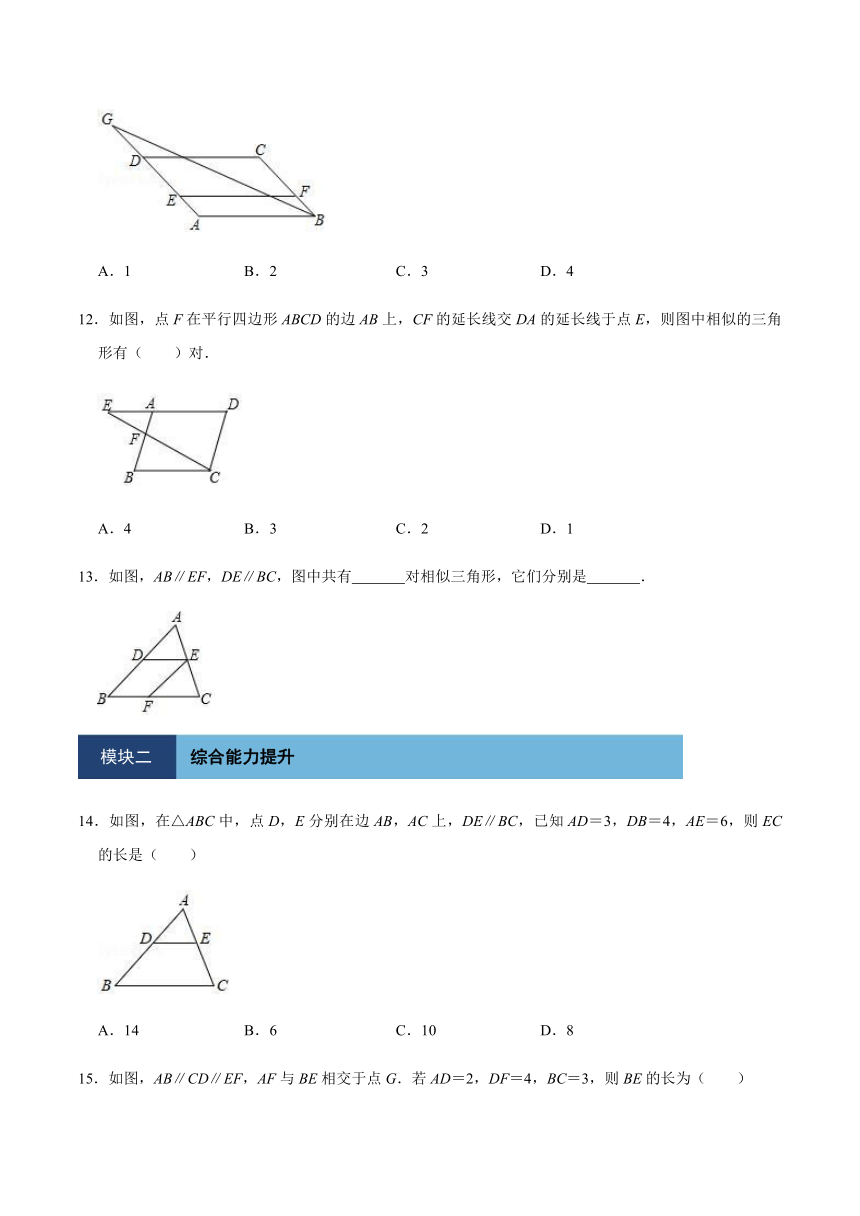
10.如图,点E是平行四边形ABCD中BC的延长线上的一点,连接AE交CD于F,交BD于M,则图中共有相似三角形(不含全等的三角形)( )对.
A.4 B.5 C.6 D.7
11.如图,在平行四边形ABCD中,点E,F分别在边AD、BC上,且EF∥CD,G为边AD延长线上一点,连接BG,则图中与△ABG相似的三角形有( )个.
A.1 B.2 C.3 D.4
12.如图,点F在平行四边形ABCD的边AB上,CF的延长线交DA的延长线于点E,则图中相似的三角形有( )对.
A.4 B.3 C.2 D.1
13.如图,AB∥EF,DE∥BC,图中共有 对相似三角形,它们分别是 .
综合能力提升
模块二
综合能力提升
模块二
14.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AD=3,DB=4,AE=6,则EC的长是( )
A.14 B.6 C.10 D.8
15.如图,AB∥CD∥EF,AF与BE相交于点G.若AD=2,DF=4,BC=3,则BE的长为( )
A.203 B.323 C.12 D.9
16.如图,已知AD∥BE∥CF,那么下列结论正确的是( )
A.BECF=DEDF B.DEEF=ABBC C.BECF=ABAC D.EFDE=ABBC
17.如图,在△ABC中,DE∥AB,且CDBD=32,则CECA的值为( )
A.35 B.23 C.45 D.32
18.如图,a∥b∥c,直线m、n与a、b、c分别相交于点A、B、C和点D、B、F.若AB=3,BC=5,DE=4,则EF的长为 .
19.如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若ABBC=23,DE=6,求EF的长.
20.如图,已知AC∥FE∥BD,求证:AEAD+BEBC=1.
参考答案与试题解析
1.解:∵△ABC∽△DEF,相似比为1:2,AB=4.
∴ABDE=12=4DE,
则DE的长是:8.
故选:D.
2.解:∵△ABC∽△DEF,∠A=30°,
∴∠D=∠A=30°.
故选:A.
3.解:∵△ABO∽△CDO,
∴BODO=ABDC,
∵BO=8,DO=4,CD=3,
∴84=AB3,
解得:AB=6.
故选:D.
4.解:∵l1∥l2∥l3,AB=3,BC=5,DE=4,
∴ABBC=DEEF,即35=4EF,
解得,EF=203,
故选:B.
5.解:∵l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F,
∴EFDF=BCAC,
又∵ABBC=32,
∴EFDF=BCAC=25,
故选:C.
6.解:∵DE∥BC,AD=4,DB=2,AE=3,
∴ADDB=AEEC,即42=3EC,
解得,EC=32,
故选:D.
7.解:∵DE∥BC,
∴EAAC=DAAB,即36=2AB,解得AB=4,
∴BD=AD+AB=2+4=6.
故选:B.
8.解:∵AC∥EF∥BD,
∴AEEB=CFFD=23,
∴FD=32CF=32×6=9,
∴CD=CF+FD=6+9=15.
故答案为15.
9.解:∵l1∥l2∥l3,
∴AB:BC=DE:EF,
∵AB=3,BC=5,DF=16,
∴3:5=DE:(16﹣DE),
∴DE=6,
∴EF=16﹣6=10.
10.解:在?ABCD中,
∵AB∥CD,
∴△ABM∽△FDM,△ABE∽△FCE,
∵AD∥BC,
∴△ADM∽△EBM,△FDA∽△FCE,
∴△ABE∽△FDA,
∴图中相似三角形有5对.
故选:B.
11.解:如图,
∵四边形ABCD为平行四边形,
∴CD∥AB,AD∥BC,
∴△DGM∽△AGB,△DGM∽△CBM,
∵EF∥CD,
∴△DGM∽△EGN,△CBM∽△FBN,
∴△DGM∽△AGB∽△FBN∽△CBM∽△EGN.
故选:D.
12.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
由AF∥CD,可以推出△EAF∽△EDC,
由AE∥BC,可以推出△AEF∽△BCF,
则△EDC∽△CBF,
故图中相似的三角形有3对.
故选:B.
13.解:∵AB∥EF,DE∥BC,
∴△ADE∽△ABC,△CEF∽△CAB,△CEF∽△EAD,
故答案为:3;△ADE∽△ABC,△CEF∽△CAB,△CEF∽△EAD
14.解:∵DE∥BC,
∴AEEC=ADDB,
即6EC=34,
解得:EC=8,
故选:D.
15.解:∵AB∥CD∥EF,
∴ADDF=BCCE,
∴ADAD+DF=BCBE,
∵AD=2,DF=4,BC=3,
∴22+4=3BE,
∴BE=9,
故选:D.
16.解:∵AD∥BE∥CF,
∴EFDE=BCAB,DEDF=ABAC,
故A、D、C错误,B正确.
故选:B.
17.解:∵CDBD=32,
∴CDCB=35,
∵DE∥AB,
∴CECA=CDCB=35,
故选:A.
18.解:∵a∥b∥c,AB=3,BC=5,DE=4,
∴ABBC=DEEF,即35=4EF,
解得,EF=203,
故答案为:203.
19.解:∵l1∥l2∥l3,
∴ABBC=DEEF,
∵ABBC=23,DE=6,
∴23=6EF,
∴EF=9.
20.证明:∵AC∥EF,
∴BEBC=BFBA①,
∵FE∥BD,
∴AEAD=AFAB②,
①+②,得:BEBC+AEAD=BFAB+AFAB=ABAB=1,
即AEAD+BEBC=1.
27.2.1 相似三角形的判定
第1课时 平行线分线段成比例
基础知识精炼
模块一
基础知识精炼
模块一
【知识点1】相似三角形及其相似比
【知识点1】相似三角形及其相似比
1.若△ABC∽△DEF,相似比为1:2,AB=4,则DE的长为( )
A.2 B.4 C.6 D.8
2.如图,若△ABC∽△DEF,则∠D的度数为( )
A.30° B.50° C.100° D.以上都不对
3.如图,△ABO∽△CDO,若BO=8,DO=4,CD=3,则AB的长是( )
A.2 B.3 C.4 D.6
【知识点2】平行线分线段成比例及其推论
【知识点2】平行线分线段成比例及其推论
4.如图,l1∥l2∥l3,直线a,b分别与l1,l2,l3相交于点A,B,C和点D,E,F,若AB=3,BC=5,DE=4,则EF的长为( )
A.323 B.203 C.223 D.8
5.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F,若ABBC=32,则EFDF的值为( )
A.32 B.35 C.25 D.52
6.如图,在△ABC中,DE∥BC,AD=4,DB=2,AE=3,则EC的长为( )
A.23 B.1 C.2 D.32
7.如图,点D、E分别在△ABC的边BA、CA的延长线上,且DE∥BC,已知AE=3,AC=6,AD=2,则BD的长为( )
A.4 B.6 C.7 D.8
8.如图,已知AC∥EF∥BD.如果AE:EB=2:3,CF=6.那么CD的长等于 .
9.已知,如图l1∥l2∥l3,AB=3,BC=5,DF=16,求DE和EF的长.
【知识点3】利用平行线判定三角形相似的定理
【知识点3】利用平行线判定三角形相似的定理
10.如图,点E是平行四边形ABCD中BC的延长线上的一点,连接AE交CD于F,交BD于M,则图中共有相似三角形(不含全等的三角形)( )对.
A.4 B.5 C.6 D.7
11.如图,在平行四边形ABCD中,点E,F分别在边AD、BC上,且EF∥CD,G为边AD延长线上一点,连接BG,则图中与△ABG相似的三角形有( )个.
A.1 B.2 C.3 D.4
12.如图,点F在平行四边形ABCD的边AB上,CF的延长线交DA的延长线于点E,则图中相似的三角形有( )对.
A.4 B.3 C.2 D.1
13.如图,AB∥EF,DE∥BC,图中共有 对相似三角形,它们分别是 .
综合能力提升
模块二
综合能力提升
模块二
14.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AD=3,DB=4,AE=6,则EC的长是( )
A.14 B.6 C.10 D.8
15.如图,AB∥CD∥EF,AF与BE相交于点G.若AD=2,DF=4,BC=3,则BE的长为( )
A.203 B.323 C.12 D.9
16.如图,已知AD∥BE∥CF,那么下列结论正确的是( )
A.BECF=DEDF B.DEEF=ABBC C.BECF=ABAC D.EFDE=ABBC
17.如图,在△ABC中,DE∥AB,且CDBD=32,则CECA的值为( )
A.35 B.23 C.45 D.32
18.如图,a∥b∥c,直线m、n与a、b、c分别相交于点A、B、C和点D、B、F.若AB=3,BC=5,DE=4,则EF的长为 .
19.如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若ABBC=23,DE=6,求EF的长.
20.如图,已知AC∥FE∥BD,求证:AEAD+BEBC=1.
参考答案与试题解析
1.解:∵△ABC∽△DEF,相似比为1:2,AB=4.
∴ABDE=12=4DE,
则DE的长是:8.
故选:D.
2.解:∵△ABC∽△DEF,∠A=30°,
∴∠D=∠A=30°.
故选:A.
3.解:∵△ABO∽△CDO,
∴BODO=ABDC,
∵BO=8,DO=4,CD=3,
∴84=AB3,
解得:AB=6.
故选:D.
4.解:∵l1∥l2∥l3,AB=3,BC=5,DE=4,
∴ABBC=DEEF,即35=4EF,
解得,EF=203,
故选:B.
5.解:∵l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F,
∴EFDF=BCAC,
又∵ABBC=32,
∴EFDF=BCAC=25,
故选:C.
6.解:∵DE∥BC,AD=4,DB=2,AE=3,
∴ADDB=AEEC,即42=3EC,
解得,EC=32,
故选:D.
7.解:∵DE∥BC,
∴EAAC=DAAB,即36=2AB,解得AB=4,
∴BD=AD+AB=2+4=6.
故选:B.
8.解:∵AC∥EF∥BD,
∴AEEB=CFFD=23,
∴FD=32CF=32×6=9,
∴CD=CF+FD=6+9=15.
故答案为15.
9.解:∵l1∥l2∥l3,
∴AB:BC=DE:EF,
∵AB=3,BC=5,DF=16,
∴3:5=DE:(16﹣DE),
∴DE=6,
∴EF=16﹣6=10.
10.解:在?ABCD中,
∵AB∥CD,
∴△ABM∽△FDM,△ABE∽△FCE,
∵AD∥BC,
∴△ADM∽△EBM,△FDA∽△FCE,
∴△ABE∽△FDA,
∴图中相似三角形有5对.
故选:B.
11.解:如图,
∵四边形ABCD为平行四边形,
∴CD∥AB,AD∥BC,
∴△DGM∽△AGB,△DGM∽△CBM,
∵EF∥CD,
∴△DGM∽△EGN,△CBM∽△FBN,
∴△DGM∽△AGB∽△FBN∽△CBM∽△EGN.
故选:D.
12.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
由AF∥CD,可以推出△EAF∽△EDC,
由AE∥BC,可以推出△AEF∽△BCF,
则△EDC∽△CBF,
故图中相似的三角形有3对.
故选:B.
13.解:∵AB∥EF,DE∥BC,
∴△ADE∽△ABC,△CEF∽△CAB,△CEF∽△EAD,
故答案为:3;△ADE∽△ABC,△CEF∽△CAB,△CEF∽△EAD
14.解:∵DE∥BC,
∴AEEC=ADDB,
即6EC=34,
解得:EC=8,
故选:D.
15.解:∵AB∥CD∥EF,
∴ADDF=BCCE,
∴ADAD+DF=BCBE,
∵AD=2,DF=4,BC=3,
∴22+4=3BE,
∴BE=9,
故选:D.
16.解:∵AD∥BE∥CF,
∴EFDE=BCAB,DEDF=ABAC,
故A、D、C错误,B正确.
故选:B.
17.解:∵CDBD=32,
∴CDCB=35,
∵DE∥AB,
∴CECA=CDCB=35,
故选:A.
18.解:∵a∥b∥c,AB=3,BC=5,DE=4,
∴ABBC=DEEF,即35=4EF,
解得,EF=203,
故答案为:203.
19.解:∵l1∥l2∥l3,
∴ABBC=DEEF,
∵ABBC=23,DE=6,
∴23=6EF,
∴EF=9.
20.证明:∵AC∥EF,
∴BEBC=BFBA①,
∵FE∥BD,
∴AEAD=AFAB②,
①+②,得:BEBC+AEAD=BFAB+AFAB=ABAB=1,
即AEAD+BEBC=1.
