2020-2021学年 人教版 九年级数学下册 27.2.2 相似三角形的性质 同步练习(Word版 含解析)
文档属性
| 名称 | 2020-2021学年 人教版 九年级数学下册 27.2.2 相似三角形的性质 同步练习(Word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 239.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-06 00:00:00 | ||
图片预览


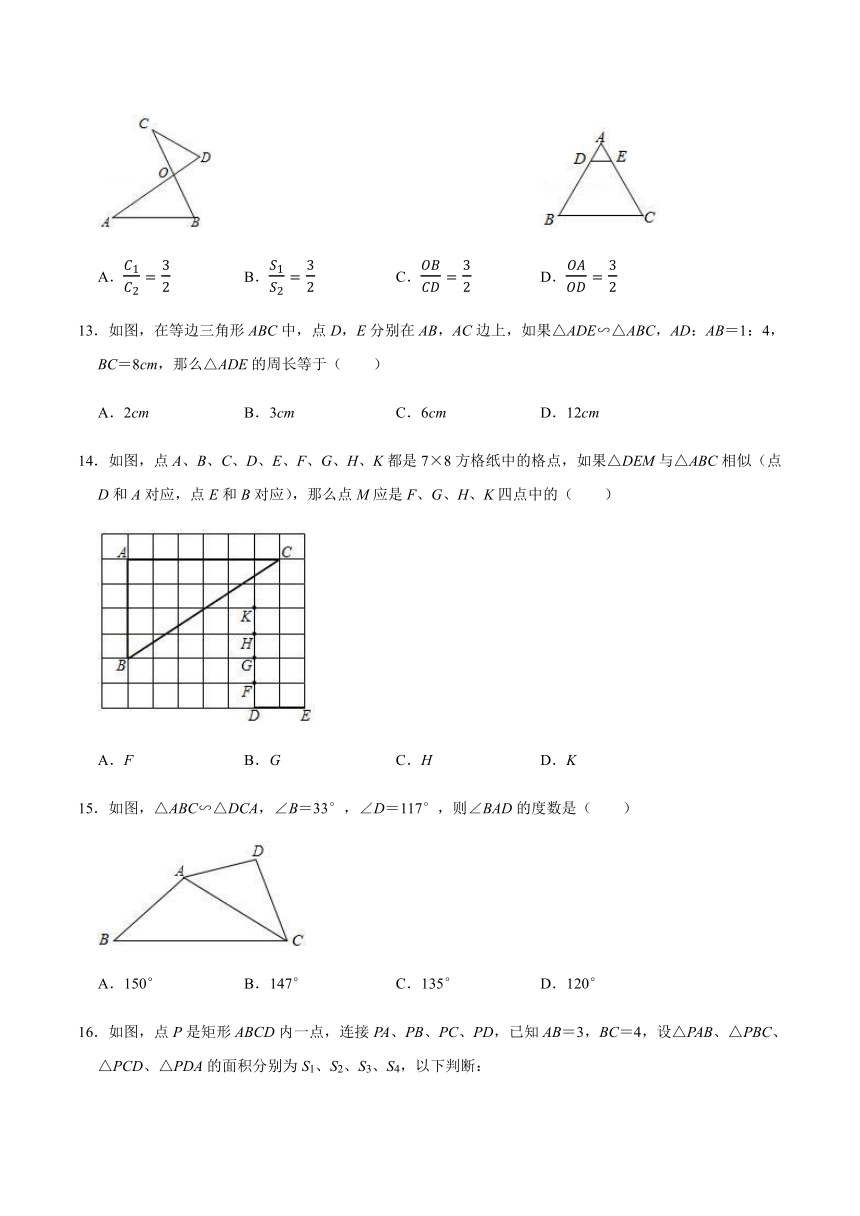

文档简介
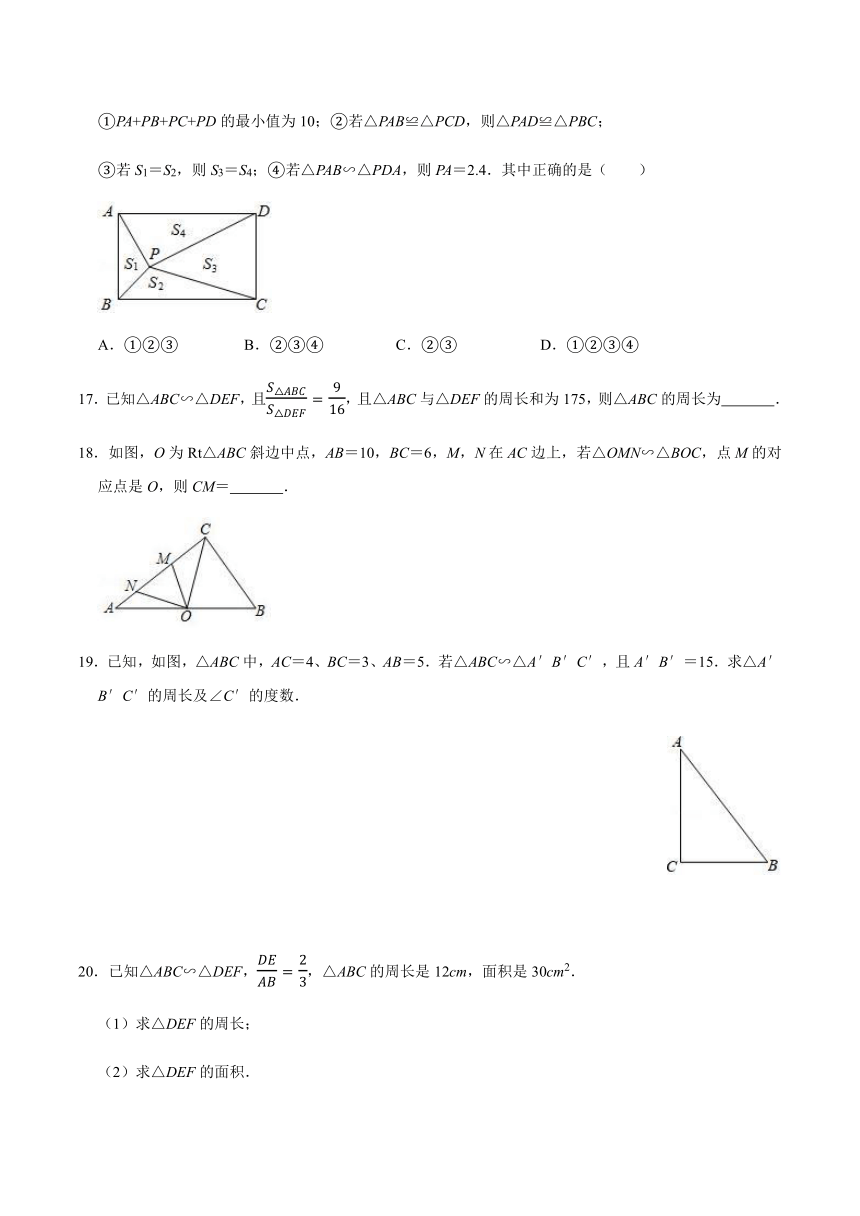
27.2 相似三角形
27.2.2 相似三角形的性质
基础知识精炼
模块一
基础知识精炼
模块一
【知识点1】相似三角形对应线段的比等于相似比
【知识点1】相似三角形对应线段的比等于相似比
1.若△ABC∽△DEF,相似比为1:2,AB=4,则DE的长为( )
A.2 B.4 C.6 D.8
2.如果两个相似三角形的对应边之比为3:7,其中一个三角形的一边上的中线长为2,则另一个三角形对应中线的长为( )
A.143 B.67 C.143或67 D.无法确定
3.已知△ABC∽△A'B'C',顶点A、B、C分别与顶点A'、B'、C'对应,AD、A'D'分别是BC、B'C'边上的中线,如果BC=3,AD=2.4,B'C'=2,那么A'D'的长是 .
【知识点2】相似三角形周长的比等于相似比
角形相似
【知识点2】相似三角形周长的比等于相似比
角形相似
4.已知△ABC与△A1B1C1相似,且相似比为3:2,则△ABC与△A1B1C1的周长比为( )
A.1:1 B.3:2 C.6:2 D.9:4
5.两个相似三角形面积比是4:9,其中一个三角形的周长为24cm,则另一个三角形的周长是( )cm.
A.16 B.16或28 C.36 D.16或36
6.如图,函数y=-1x(x<0)的图象经过Rt△ABO斜边OB的中点D,与直角边AB相交于C,连结AD.若AD=3,则△ABO的周长为( )
A.12 B.6+38 C.6+210 D.6+211
7.已知△ABC与△DEF相似,如果△ABC三边长分别为5,7,8,△DEF的最长边与最短边的差为9,那么△DEF的周长是 .
【知识点3】相似三角形面积的比等于相似比的平方
角形相似
【知识点3】相似三角形面积的比等于相似比的平方
角形相似
8.两个相似三角形的面积比为1:16,则它们对应边的比是( )
A.1:16 B.1:8 C.1:4 D.4:1
9.已知△ABC∽△DEF,AB=3,DE=5,则△ABC与△DEF的面积之比为( )
A.925 B.35 C.53 D.259
10.已知△ABC∽△A′B′C′,ABA′B′=34,则△ABC与△A′B′C′的面积之比为( )
A.34 B.43 C.916 D.169
11.两个相似三角形的相似比为1:2,其中一个三角形的面积是4,则另一个三角形的面积是 .
综合能力提升
模块二
综合能力提升
模块二
12.如图,△OAB∽△OCD,OA:OC=3:2,△OAB与△OCD的面积分别是S1与S2,周长分别是C1与C2,则下列说法正确的是( )
A.C1C2=32 B.S1S2=32 C.OBCD=32 D.OAOD=32
13.如图,在等边三角形ABC中,点D,E分别在AB,AC边上,如果△ADE∽△ABC,AD:AB=1:4,BC=8cm,那么△ADE的周长等于( )
A.2cm B.3cm C.6cm D.12cm
14.如图,点A、B、C、D、E、F、G、H、K都是7×8方格纸中的格点,如果△DEM与△ABC相似(点D和A对应,点E和B对应),那么点M应是F、G、H、K四点中的( )
A.F B.G C.H D.K
15.如图,△ABC∽△DCA,∠B=33°,∠D=117°,则∠BAD的度数是( )
A.150° B.147° C.135° D.120°
16.如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4,以下判断:
①PA+PB+PC+PD的最小值为10;②若△PAB≌△PCD,则△PAD≌△PBC;
③若S1=S2,则S3=S4;④若△PAB∽△PDA,则PA=2.4.其中正确的是( )
A.①②③ B.②③④ C.②③ D.①②③④
17.已知△ABC∽△DEF,且S△ABCS△DEF=916,且△ABC与△DEF的周长和为175,则△ABC的周长为 .
18.如图,O为Rt△ABC斜边中点,AB=10,BC=6,M,N在AC边上,若△OMN∽△BOC,点M的对应点是O,则CM= .
19.已知,如图,△ABC中,AC=4、BC=3、AB=5.若△ABC∽△A′B′C′,且A′B′=15.求△A′B′C′的周长及∠C′的度数.
20.已知△ABC∽△DEF,DEAB=23,△ABC的周长是12cm,面积是30cm2.
(1)求△DEF的周长;
(2)求△DEF的面积.
21.如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=14DC,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求FG的长.
22.如图,在△ABC中,点D为边BC上一点,且AD=AB,AE⊥BC,垂足为点E.过点D作DF∥AB,交边AC于点F,连接EF,EF2=12BD?EC.
(1)求证:△EDF∽△EFC;
(2)如果S△EDFS△ADC=14,求证:AB=BD.
参考答案与试题解析
1.解:∵△ABC∽△DEF,相似比为1:2,AB=4.
∴ABDE=12=4DE,
则DE的长是:8.
故选:D.
2.解:∵相似三角形的对应边之比为3:7,
∴它们的对应中线的比为3:7,
∵其中一个三角形的一条中线为2,而这条中线可能是小三角形的,也可能是大三角形的,
∴另一个三角形对应的中线可能为143,也可能是67.
故选:C.
3.解:∵△ABC∽△A'B'C',AD和A'D'是它们的对应中线,BC=3,AD=2.4,B'C'=2,
∴BC:B′C′=AD:A′D′,
∴2.4:A′D′=3:2,
∴A'D'的长是1.6,
故答案为:1.6.
4.解:∵△ABC∽△A1B1C1,且相似比为3:2,
∴△ABC与△A1B1C1的周长比为3:2,
故选:B.
5.解:∵两个相似三角形面积比是4:9,
∴两个相似三角形相似比是2:3,
∴两个相似三角形周长比是2:3,
∵一个三角形的周长为24cm,
∴另一个三角形的周长是16cm或36cm,
故选:D.
6.解:如图,过点D作DE⊥AO于E,
∵点D是BO的中点,
∴AD=BD=DO=3,
∴BO=6,
∵DE⊥AO,AB⊥AO,
∴AB∥DE,
∴DOBO=DEAB=EOAO=12,
∴AB=2DE,AO=2EO,
∵S△DEO=12DE×EO=12,
∴S△ABO=12AB×AO=2,
∵AB2+AO2=OB2=36,
∴(AB+AO)2=36+8,
∴AB+AO=211,
∴△ABO的周长=AO+BO+AB=6+211,
故选:D.
7.解:设△DEF的最长边为x,最短边为y,依题意,则有:
x:y=8:5x-y=9,解得:x=24,y=15;
∴△ABC和△DEF的相似比为1:3,周长比也是1:3;
∵△ABC的周长=5+7+8=20,
∴△DEF的周长为60,
故答案为:60.
8.解:∵两个相似三角形的面积比为1:16,
∴它们的对应边的比=1:4.
故选:C.
9.解:∵△ABC∽△DEF,AB=3,DE=5,
∴相似比为AB:DE=3:5,
∴其面积之比为9:25.
故选:A.
10.解:∵△ABC∽△A′B′C′,ABA′B′=34,
∴△ABC与△A′B′C′的面积比=(34)2=916,
故选:C.
11.解:∵两个相似三角形的相似比为1:2,
∴它们的面积面积比为:1:4,
∵其中一个三角形的面积为4,
∴若小三角形的面积为4,则另一个三角形的面积为16;
若大三角形的面积为4,则另一个三角形的面积为1.
∴另一个三角形的面积为16或1.
故答案为:16或1.
12.解:∵△OAB∽△OCD,OA:OC=3:2,
∴C1C2=32,A正确;
∴S1S2=94,B错误;
∴OBOD=32,C错误;
∴OA:OC=3:2,D错误;
故选:A.
13.解:∵点D、E分别在AB、AC边上,且DE∥BC
∴△ADE∽△ABC
∵AD:AB=1:4
∴其周长比为1:4
∵BC=8cm,三角形ABC为等边三角形
∴△ABC的周长为24cm
∴△ADE的周长为6cm.
故选:C.
14.解:根据题意,
△DEM∽△ABC,AB=4,AC=6 DE=2,
∴DE:AB=DM:AC,
∴DM=3,
∴M应是H,
故选:C.
15.解:∵△ABC∽△DCA,
∴∠BAC=∠D=117°,∠DCA=∠B=33°,
∴∠DAC=180°﹣117°﹣33°=30°,
∴∠BAD=∠BAC+∠DAC=147°,
故选:B.
16.解:①当点P是矩形ABCD两对角线的交点时,PA+PB+PC+PD的值最小,根据勾股定理得,AC=BD=5,所以PA+PB+PC+PD的最小值为10,故①正确;
②若△PAB≌△PCD,则PA=PC,PB=PD,所以P在线段AC、BD的垂直平分线上,即P是矩形ABCD两对角线的交点,所以△PAD≌△PBC,故②正确;
③如图,若S1=S2,
过点P作PH⊥BC于H,HP的延长线交AD于G,
则PG⊥AD.
∴四边形ABHG是矩形,
∴GH=AB,
436435581915∴S2+S4=12AD?PG+12BC?PH=12BC?(PH+PG)=12BC?GH=12BC?AB,
过点P作PM⊥AB于M,MP的延长线交CD于N,
同理S1+S3=12BC?AB,
∴S1+S3=S2+S4,则S3=S4,故③正确;
④若△PAB~△PDA,则∠PAB=∠PDA,∠PAB+∠PAD=∠PDA+∠PAD=90°,∠APD=180°﹣(∠PDA+∠PAD)=90°,同理可得∠APB=90°,那么∠BPD=180°,B、P、D三点共线,PA是直角△BAD斜边上的高,根据面积公式可得PA=2.4,故④正确.
故选:D.
17.解:∵△ABC∽△DEF,且S△ABCS△DEF=916,
∴△ABC与△DEF的周长的比为3:4,
∵△ABC与△DEF的周长和为175,
∴△ABC的周长为175×33+4=75,
故答案为:75.
18.解:∵△OMN∽△BOC,
∴∠NMO=∠BOC,
3488690205105∴∠AOC=∠CMO,
∵∠BOC=∠OMN,
又∵∠MCO=∠OCA,
∴△OCM∽△ACO,
∴OC2=CM?CA,
∴25=CM?8,
∴CM=258.
故答案为:258.
19.解:∵AC=4,BC=3,AB=5,
∴AC2+BC2=25=AB2,△ABC的周长为12,
∴∠C=90°,
∵△ABC∽△A′B′C′,且A′B′=15,
∴相似比=515=13,∠C=∠C',
∴△ABC的周长为12×3=36,∠C'的度数为90°.
20.解:(1)∵DEAB=23,
∴△DEF的周长=12×23=8(cm);
(2)∵DEAB=23,
∴△DEF的面积=30×(23)2=1313(cm2).
21.(1)证明:∵四边形ABCD为正方形,
∴AD=AB=DC=BC,∠A=∠D=90°,
∵AE=ED,
∴AEAB=12,
∵DF=14DC,
∴DFDE=12,
∴AEAB=DFDE,
∴△ABE∽△DEF;
(2)∵四边形ABCD为正方形,
∴ED∥BG,
∴△DEF∽△CGF,
∴EDCG=DFCF,
又∵DF=14DC,正方形的边长为4,
∴DF=1,ED=2,
∴CF=3,CG=6,
∴GF=CF2+CG2=9+36=35.
22.证明:(1)∵AB=AD,AE⊥BC,
∴BE=ED=12DB;
∵EF2=12?BD?EC,
∴EF2=ED?EC,即得 EFEC=EDEF,
又∵∠FED=∠CEF,
∴△EDF∽△EFC.
(2)∵AB=AD,
∴∠B=∠ADB,
又∵DF∥AB,
∴∠FDC=∠B,
∴∠ADB=∠FDC,
∴∠ADB+∠ADF=∠FDC+∠ADF,即得∠EDF=∠ADC;
∵△EDF∽△EFC,
∴∠EFD=∠C,
∴△EDF∽△ADC,
∴S△EDFS△ADC=(EDAD)2=14,
∴EDAD=12,即 ED=12AD;
又∵ED=BE=12BD,
∴BD=AD,
∴AB=BD.
27.2.2 相似三角形的性质
基础知识精炼
模块一
基础知识精炼
模块一
【知识点1】相似三角形对应线段的比等于相似比
【知识点1】相似三角形对应线段的比等于相似比
1.若△ABC∽△DEF,相似比为1:2,AB=4,则DE的长为( )
A.2 B.4 C.6 D.8
2.如果两个相似三角形的对应边之比为3:7,其中一个三角形的一边上的中线长为2,则另一个三角形对应中线的长为( )
A.143 B.67 C.143或67 D.无法确定
3.已知△ABC∽△A'B'C',顶点A、B、C分别与顶点A'、B'、C'对应,AD、A'D'分别是BC、B'C'边上的中线,如果BC=3,AD=2.4,B'C'=2,那么A'D'的长是 .
【知识点2】相似三角形周长的比等于相似比
角形相似
【知识点2】相似三角形周长的比等于相似比
角形相似
4.已知△ABC与△A1B1C1相似,且相似比为3:2,则△ABC与△A1B1C1的周长比为( )
A.1:1 B.3:2 C.6:2 D.9:4
5.两个相似三角形面积比是4:9,其中一个三角形的周长为24cm,则另一个三角形的周长是( )cm.
A.16 B.16或28 C.36 D.16或36
6.如图,函数y=-1x(x<0)的图象经过Rt△ABO斜边OB的中点D,与直角边AB相交于C,连结AD.若AD=3,则△ABO的周长为( )
A.12 B.6+38 C.6+210 D.6+211
7.已知△ABC与△DEF相似,如果△ABC三边长分别为5,7,8,△DEF的最长边与最短边的差为9,那么△DEF的周长是 .
【知识点3】相似三角形面积的比等于相似比的平方
角形相似
【知识点3】相似三角形面积的比等于相似比的平方
角形相似
8.两个相似三角形的面积比为1:16,则它们对应边的比是( )
A.1:16 B.1:8 C.1:4 D.4:1
9.已知△ABC∽△DEF,AB=3,DE=5,则△ABC与△DEF的面积之比为( )
A.925 B.35 C.53 D.259
10.已知△ABC∽△A′B′C′,ABA′B′=34,则△ABC与△A′B′C′的面积之比为( )
A.34 B.43 C.916 D.169
11.两个相似三角形的相似比为1:2,其中一个三角形的面积是4,则另一个三角形的面积是 .
综合能力提升
模块二
综合能力提升
模块二
12.如图,△OAB∽△OCD,OA:OC=3:2,△OAB与△OCD的面积分别是S1与S2,周长分别是C1与C2,则下列说法正确的是( )
A.C1C2=32 B.S1S2=32 C.OBCD=32 D.OAOD=32
13.如图,在等边三角形ABC中,点D,E分别在AB,AC边上,如果△ADE∽△ABC,AD:AB=1:4,BC=8cm,那么△ADE的周长等于( )
A.2cm B.3cm C.6cm D.12cm
14.如图,点A、B、C、D、E、F、G、H、K都是7×8方格纸中的格点,如果△DEM与△ABC相似(点D和A对应,点E和B对应),那么点M应是F、G、H、K四点中的( )
A.F B.G C.H D.K
15.如图,△ABC∽△DCA,∠B=33°,∠D=117°,则∠BAD的度数是( )
A.150° B.147° C.135° D.120°
16.如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4,以下判断:
①PA+PB+PC+PD的最小值为10;②若△PAB≌△PCD,则△PAD≌△PBC;
③若S1=S2,则S3=S4;④若△PAB∽△PDA,则PA=2.4.其中正确的是( )
A.①②③ B.②③④ C.②③ D.①②③④
17.已知△ABC∽△DEF,且S△ABCS△DEF=916,且△ABC与△DEF的周长和为175,则△ABC的周长为 .
18.如图,O为Rt△ABC斜边中点,AB=10,BC=6,M,N在AC边上,若△OMN∽△BOC,点M的对应点是O,则CM= .
19.已知,如图,△ABC中,AC=4、BC=3、AB=5.若△ABC∽△A′B′C′,且A′B′=15.求△A′B′C′的周长及∠C′的度数.
20.已知△ABC∽△DEF,DEAB=23,△ABC的周长是12cm,面积是30cm2.
(1)求△DEF的周长;
(2)求△DEF的面积.
21.如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=14DC,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求FG的长.
22.如图,在△ABC中,点D为边BC上一点,且AD=AB,AE⊥BC,垂足为点E.过点D作DF∥AB,交边AC于点F,连接EF,EF2=12BD?EC.
(1)求证:△EDF∽△EFC;
(2)如果S△EDFS△ADC=14,求证:AB=BD.
参考答案与试题解析
1.解:∵△ABC∽△DEF,相似比为1:2,AB=4.
∴ABDE=12=4DE,
则DE的长是:8.
故选:D.
2.解:∵相似三角形的对应边之比为3:7,
∴它们的对应中线的比为3:7,
∵其中一个三角形的一条中线为2,而这条中线可能是小三角形的,也可能是大三角形的,
∴另一个三角形对应的中线可能为143,也可能是67.
故选:C.
3.解:∵△ABC∽△A'B'C',AD和A'D'是它们的对应中线,BC=3,AD=2.4,B'C'=2,
∴BC:B′C′=AD:A′D′,
∴2.4:A′D′=3:2,
∴A'D'的长是1.6,
故答案为:1.6.
4.解:∵△ABC∽△A1B1C1,且相似比为3:2,
∴△ABC与△A1B1C1的周长比为3:2,
故选:B.
5.解:∵两个相似三角形面积比是4:9,
∴两个相似三角形相似比是2:3,
∴两个相似三角形周长比是2:3,
∵一个三角形的周长为24cm,
∴另一个三角形的周长是16cm或36cm,
故选:D.
6.解:如图,过点D作DE⊥AO于E,
∵点D是BO的中点,
∴AD=BD=DO=3,
∴BO=6,
∵DE⊥AO,AB⊥AO,
∴AB∥DE,
∴DOBO=DEAB=EOAO=12,
∴AB=2DE,AO=2EO,
∵S△DEO=12DE×EO=12,
∴S△ABO=12AB×AO=2,
∵AB2+AO2=OB2=36,
∴(AB+AO)2=36+8,
∴AB+AO=211,
∴△ABO的周长=AO+BO+AB=6+211,
故选:D.
7.解:设△DEF的最长边为x,最短边为y,依题意,则有:
x:y=8:5x-y=9,解得:x=24,y=15;
∴△ABC和△DEF的相似比为1:3,周长比也是1:3;
∵△ABC的周长=5+7+8=20,
∴△DEF的周长为60,
故答案为:60.
8.解:∵两个相似三角形的面积比为1:16,
∴它们的对应边的比=1:4.
故选:C.
9.解:∵△ABC∽△DEF,AB=3,DE=5,
∴相似比为AB:DE=3:5,
∴其面积之比为9:25.
故选:A.
10.解:∵△ABC∽△A′B′C′,ABA′B′=34,
∴△ABC与△A′B′C′的面积比=(34)2=916,
故选:C.
11.解:∵两个相似三角形的相似比为1:2,
∴它们的面积面积比为:1:4,
∵其中一个三角形的面积为4,
∴若小三角形的面积为4,则另一个三角形的面积为16;
若大三角形的面积为4,则另一个三角形的面积为1.
∴另一个三角形的面积为16或1.
故答案为:16或1.
12.解:∵△OAB∽△OCD,OA:OC=3:2,
∴C1C2=32,A正确;
∴S1S2=94,B错误;
∴OBOD=32,C错误;
∴OA:OC=3:2,D错误;
故选:A.
13.解:∵点D、E分别在AB、AC边上,且DE∥BC
∴△ADE∽△ABC
∵AD:AB=1:4
∴其周长比为1:4
∵BC=8cm,三角形ABC为等边三角形
∴△ABC的周长为24cm
∴△ADE的周长为6cm.
故选:C.
14.解:根据题意,
△DEM∽△ABC,AB=4,AC=6 DE=2,
∴DE:AB=DM:AC,
∴DM=3,
∴M应是H,
故选:C.
15.解:∵△ABC∽△DCA,
∴∠BAC=∠D=117°,∠DCA=∠B=33°,
∴∠DAC=180°﹣117°﹣33°=30°,
∴∠BAD=∠BAC+∠DAC=147°,
故选:B.
16.解:①当点P是矩形ABCD两对角线的交点时,PA+PB+PC+PD的值最小,根据勾股定理得,AC=BD=5,所以PA+PB+PC+PD的最小值为10,故①正确;
②若△PAB≌△PCD,则PA=PC,PB=PD,所以P在线段AC、BD的垂直平分线上,即P是矩形ABCD两对角线的交点,所以△PAD≌△PBC,故②正确;
③如图,若S1=S2,
过点P作PH⊥BC于H,HP的延长线交AD于G,
则PG⊥AD.
∴四边形ABHG是矩形,
∴GH=AB,
436435581915∴S2+S4=12AD?PG+12BC?PH=12BC?(PH+PG)=12BC?GH=12BC?AB,
过点P作PM⊥AB于M,MP的延长线交CD于N,
同理S1+S3=12BC?AB,
∴S1+S3=S2+S4,则S3=S4,故③正确;
④若△PAB~△PDA,则∠PAB=∠PDA,∠PAB+∠PAD=∠PDA+∠PAD=90°,∠APD=180°﹣(∠PDA+∠PAD)=90°,同理可得∠APB=90°,那么∠BPD=180°,B、P、D三点共线,PA是直角△BAD斜边上的高,根据面积公式可得PA=2.4,故④正确.
故选:D.
17.解:∵△ABC∽△DEF,且S△ABCS△DEF=916,
∴△ABC与△DEF的周长的比为3:4,
∵△ABC与△DEF的周长和为175,
∴△ABC的周长为175×33+4=75,
故答案为:75.
18.解:∵△OMN∽△BOC,
∴∠NMO=∠BOC,
3488690205105∴∠AOC=∠CMO,
∵∠BOC=∠OMN,
又∵∠MCO=∠OCA,
∴△OCM∽△ACO,
∴OC2=CM?CA,
∴25=CM?8,
∴CM=258.
故答案为:258.
19.解:∵AC=4,BC=3,AB=5,
∴AC2+BC2=25=AB2,△ABC的周长为12,
∴∠C=90°,
∵△ABC∽△A′B′C′,且A′B′=15,
∴相似比=515=13,∠C=∠C',
∴△ABC的周长为12×3=36,∠C'的度数为90°.
20.解:(1)∵DEAB=23,
∴△DEF的周长=12×23=8(cm);
(2)∵DEAB=23,
∴△DEF的面积=30×(23)2=1313(cm2).
21.(1)证明:∵四边形ABCD为正方形,
∴AD=AB=DC=BC,∠A=∠D=90°,
∵AE=ED,
∴AEAB=12,
∵DF=14DC,
∴DFDE=12,
∴AEAB=DFDE,
∴△ABE∽△DEF;
(2)∵四边形ABCD为正方形,
∴ED∥BG,
∴△DEF∽△CGF,
∴EDCG=DFCF,
又∵DF=14DC,正方形的边长为4,
∴DF=1,ED=2,
∴CF=3,CG=6,
∴GF=CF2+CG2=9+36=35.
22.证明:(1)∵AB=AD,AE⊥BC,
∴BE=ED=12DB;
∵EF2=12?BD?EC,
∴EF2=ED?EC,即得 EFEC=EDEF,
又∵∠FED=∠CEF,
∴△EDF∽△EFC.
(2)∵AB=AD,
∴∠B=∠ADB,
又∵DF∥AB,
∴∠FDC=∠B,
∴∠ADB=∠FDC,
∴∠ADB+∠ADF=∠FDC+∠ADF,即得∠EDF=∠ADC;
∵△EDF∽△EFC,
∴∠EFD=∠C,
∴△EDF∽△ADC,
∴S△EDFS△ADC=(EDAD)2=14,
∴EDAD=12,即 ED=12AD;
又∵ED=BE=12BD,
∴BD=AD,
∴AB=BD.
