2020-2021学年人教版 九年级数学下册 27.2.3 相似三角形应用举例 同步练习(Word版 含解析)
文档属性
| 名称 | 2020-2021学年人教版 九年级数学下册 27.2.3 相似三角形应用举例 同步练习(Word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 432.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-06 06:18:08 | ||
图片预览



文档简介
27.2 相似三角形
27.2.3 相似三角形应用举例
基础知识精炼
模块一
基础知识精炼
模块一
【知识点1】利用相似三角形测量物体的高度
【知识点1】利用相似三角形测量物体的高度
1.某数学兴趣小组来到城关区时代广场,设计用手电来测量广场附近某大厦CD的高度,如图,点P处放一水平的平面镜.光线从点A出发经平面镜反射后刚好射到大厦CD的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=1.5米,BP=2米,PD=52米,那么该大厦的高度约为( )
A.39米 B.30米 C.24米 D.15米
2.如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高为1.5m,测得AB=3m,BC=7m,则建筑物CD的高是( )
A.3.5m B.4m C.4.5m D.5m
3.高4米的旗杆在水平地面上的影长为6米,此时测得附近一个建筑物的影长24米,则该建筑物的高度为( )
A.10米 B.16米 C.26米 D.36米
4.如图,为了测量旗杆的高度,某综合实践小组设计了以下方案:用2.5m长的竹竿做测量工具,移动竹竿,保持竹竿与旗杆平行,使竹竿、旗杆的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距5m、与旗杆相距20m,则旗杆的高度为 m.
【知识点2】利用相似三角形测量平面内两点的距离
角形相似
【知识点2】利用相似三角形测量平面内两点的距离
角形相似
5.如图,A,B两点被一河隔开,为了测量A,B两点间的距离,小明过点B作BF⊥AB,在BF上取两点C,D,使BC=2CD,过点D作DE⊥BF且使点A,C,E在同一条直线上,测得DE=20m,则A,B两点间的距离是( )
A.60m B.50m C.40m D.30m
6.我国古代数学著作中记载了一个问题:“今有邑方不知大小,各开中门,出北门四十步有木,出西门八百一十步见木,问:邑方几何?”其大意是:一座正方形城池,西、北边正中各开一道门,从北门往正北方向走40步后刚好有一树木,若从西门往正西方向走810步后正好看到树木,则正方形城池的边长为( )步.
A.360 B.270 C.180 D.90
7.如图,A、B两地之间有一池塘,要测量A、B两地之间的距离.选择一点O,连接AO并延长到点C,使OC=12AO,连接BO并延长到点D,使OD=12BO.测得C、D间距离为30米,则A、B两地之间的距离为( )
A.30米 B.45米 C.60米 D.90米
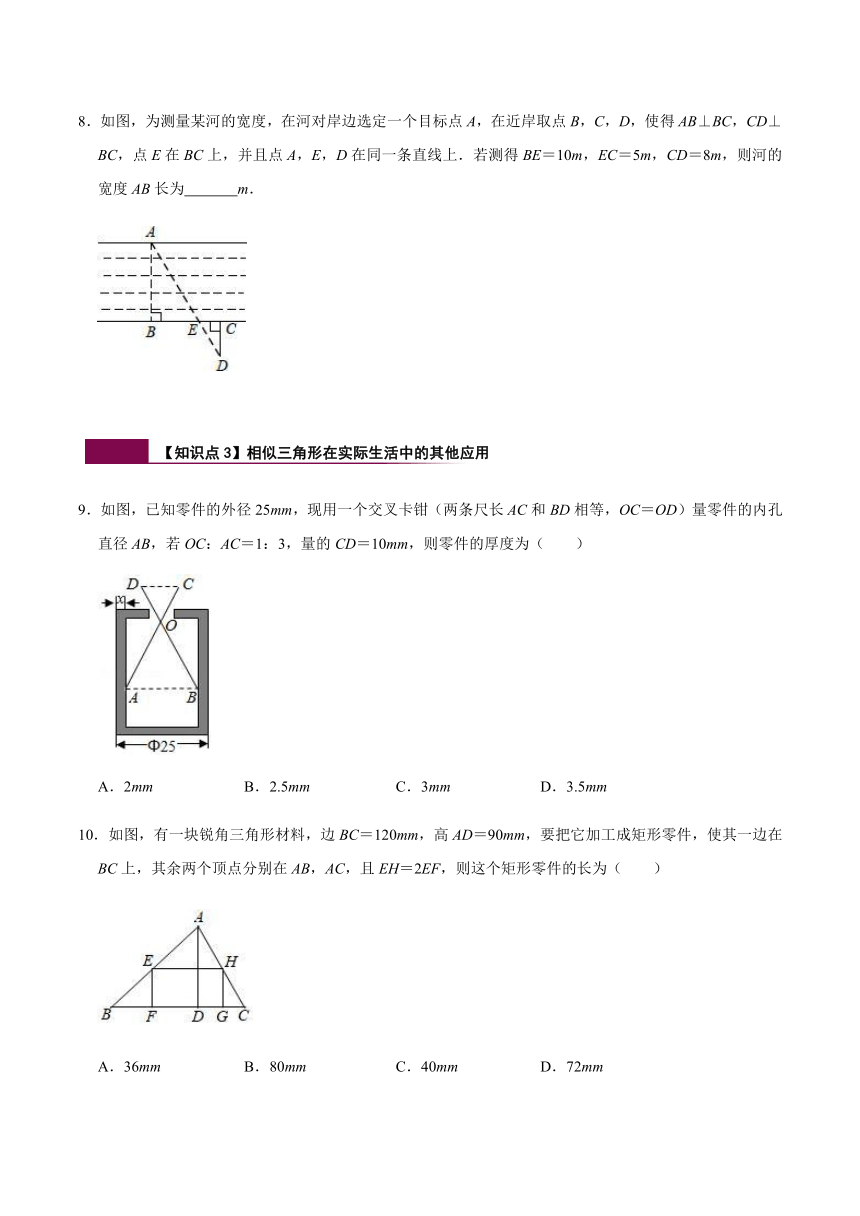
8.如图,为测量某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=10m,EC=5m,CD=8m,则河的宽度AB长为 m.
【知识点3】相似三角形在实际生活中的其他应用
角形相似
【知识点3】相似三角形在实际生活中的其他应用
角形相似
9.如图,已知零件的外径25mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB,若OC:AC=1:3,量的CD=10mm,则零件的厚度为( )
A.2mm B.2.5mm C.3mm D.3.5mm
10.如图,有一块锐角三角形材料,边BC=120mm,高AD=90mm,要把它加工成矩形零件,使其一边在BC上,其余两个顶点分别在AB,AC,且EH=2EF,则这个矩形零件的长为( )
A.36mm B.80mm C.40mm D.72mm
11.我国古代数学《九章算术》中,有个“井深几何”问题:今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸(1尺=10寸),问井深几何?其意思如图所示,则井深BD的长为( )
A.12尺 B.56尺5寸 C.57尺5寸 D.62尺5寸
12.如图,测量小玻璃管口径的量具ABC,AB的长为12cm,AC被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(DE∥AB),那么小玻璃管口径DE是( )
A.8cm B.10cm C.20cm D.60cm
13.如图,铁道口的栏杆短臂OA长1.2m,长臂OB长19.2m.当长臂外端B升高8m时,短臂外端A下降
( )
A.1.1m B.1m C.0.5m D.0.4m
综合能力提升
模块二
综合能力提升
模块二
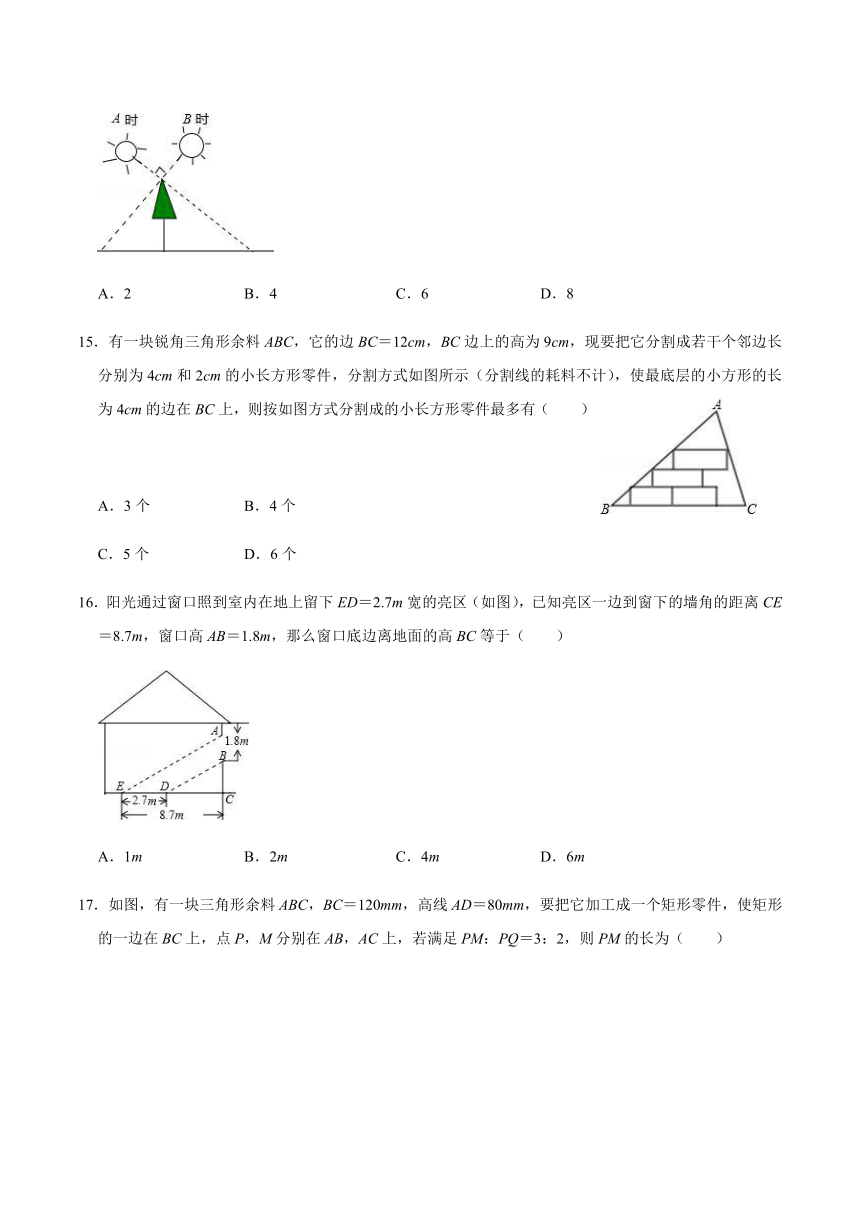
14.如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为( )m.
A.2 B.4 C.6 D.8
459295565722515.有一块锐角三角形余料ABC,它的边BC=12cm,BC边上的高为9cm,现要把它分割成若干个邻边长分别为4cm和2cm的小长方形零件,分割方式如图所示(分割线的耗料不计),使最底层的小方形的长为4cm的边在BC上,则按如图方式分割成的小长方形零件最多有( )
A.3个 B.4个
C.5个 D.6个
16.阳光通过窗口照到室内在地上留下ED=2.7m宽的亮区(如图),已知亮区一边到窗下的墙角的距离CE=8.7m,窗口高AB=1.8m,那么窗口底边离地面的高BC等于( )
A.1m B.2m C.4m D.6m
17.如图,有一块三角形余料ABC,BC=120mm,高线AD=80mm,要把它加工成一个矩形零件,使矩形的一边在BC上,点P,M分别在AB,AC上,若满足PM:PQ=3:2,则PM的长为( )
A.60mm B.16013mm C.20mm D.24013mm
18.如图,网高AB为0.8米,击球点到网的水平距离AC为3米,小明在打网球时,要使球恰好能打过网,且落点恰好在离网水平距离OA为4米,则球拍击球的高度CD为 米.
19.如图是用杠杆撬石头的示意图,C是支点,当用力压杠杆的A端时,杠杆绕C点转动,另一端B向上翘起,石头就被撬动.现有一块石头,要使其滚动,杠杆的B端必须向上翘起10cm,已知杠杆的动力臂AC与阻力臂BC之比为6:1,要使这块石头滚动,至少要将杠杆的A端向下压 cm.
20.为了估计河的宽度,勘测人员在河的对岸选定一个目标点A,在近岸分别取点B、D、E、C,使点A、B、D在一条直线上,且AD⊥DE,点A、C、E也在一条直线上,且DE∥BC.经测量BC=25米,BD=12米,DE=40米,求河的宽度AB为多少米?
21.如图,小明同学为了测量教学楼的高度OE,先在操场上点A处放一面镜子,从点A处后退1m到点B处,恰好在镜子中看到楼的顶部E点;再将镜子向后移动4m放在C处,从点C处向后退1.5m到点D处,恰好再次在镜子中看到楼的顶部E点,测得小明的眼睛距地面的高度FB,GD为1.5m,点O,A,B,C,D在同一水平线上,镜子可看成一个点.求教学楼的高度OE.
22.如图,小华和同伴春游时,发现在某地小山坡的点E处有一棵小桃树,他们想利用皮尺、测倾器和平面镜测量小桃树到山脚下的距离(即DE的长度),小华站在点B处,让同伴移动平面镜至点C处,此时小华在平面镜内可以看到点E,且测得BC=6米,CD=24米,∠CDE=135°.已知小华的身高AB=1.5米,请根据以上数据,求DE的长度(结果保留根号)
23.△ABC是一块直角三角形余料,∠C=90°,AC=8cm,BC=6cm,如图将它加工成正方形零件,试说明哪种方法利用率高?(得到的正方形的面积较大)
参考答案与试题解析
1.解:根据题意,得到:△ABP∽△PDC.
即CDAB=PDBP,
故CD=PDBP×AB=522×1.5=39米;
那么该大厦的高度是39米.
故选:A.
2.解:∵EB⊥AC,DC⊥AC,
∴EB∥DC,
∴△ABE∽△ACD,
∴ABAC=BECD,
∵BE=1.5m,AB=3m,BC=7m,
∴AC=AB+BC=10m,
∴310=1.5DC,
解得,DC=5,
即建筑物CD的高是5m,
故选:D.
3.解:设建筑物的高是x米.则x24=46,
解得:x=16.
故该建筑物的高为16米.
故选:B.
4.解:由图可知:
设旗杆的高度为x米,
竹竿高竹竿影长=旗杆高旗杆影长,
2.55=x5+20
解得x=12.5.
故答案为12.5.
5.解:∵AB⊥BF,ED⊥BF,
∴AB∥DE,
∴△ABC∽△EDC,
∴ABDE=BCCD,
即AB20=21,
解得:AB=40,
故选:C.
6.解:如图,设正方形城池的边长为x步,则AE=CE=12x,
3211830174625∵AE∥CD,
∴∠BEA=∠EDC,
∴Rt△BEA∽Rt△EDC,
∴ABEC=AECD,即4012x=12x810,
∴x=360,
即正方形城池的边长为360步.
故选:A.
7.解:∵△ABO和△COD中,OCOA=ODOB=12,
且∠AOB=∠COD,
∴△AOB∽△COD,
∴ABCD=2,
又∵CD=30m,
∴AB=60m.
故选:C.
8.解:∵AB⊥BC,CD⊥BC,
∴∠ABE=∠DCE=90°,
又∵∠AEB=∠DEC(对顶角相等),
∴△ABE∽△DCE,
∴ABCD=BECE,
即AB8=105,
解得AB=16m.
故答案为:16.
9.解:∵两条尺长AC和BD相等,OC=OD,
∴OA=OB,
∵OC:AC=1:3,
∴OC:OA=1:2,
∴OD:OB=OC:OA=1:2,
∵∠COD=∠AOB,
∴△AOB∽△COD,
∴CD:AB=OC:OA=1:2,
∵CD=10mm,
∴AB=20(mm),
∴2x+20=25,
∴x=2.5(mm),
故选:B.
10.解:设边宽为xmm,则长为2xmm,
∵四边形EFGH为矩形,
∴EH∥BC,EF∥AD,
∴EFAD=BEBA,EHBC=AEAB,
∵BE+AE=AB,
∴x90=BEAB,2x120=AEAB,
∴x90+2x120=1,
解得:x=36mm,
∴EF=36mm,EH=72mm,
故选:D.
11.解:∵BC∥DE,
∴△ABC∽△ADE,
3769995-15875∴AB:AD=BC:DE,
即5:AD=0.4:5,
解得AD=62.5,
BD=AD﹣AB=62.5﹣5=57.5尺.
故选:C.
12.解:∵DE∥AB
∴CD:AC=DE:AB
∴40:60=DE:12
∴DE=8cm
故选:A.
13.解:设短臂外端A下降x米,
则8x=19.21.2,
∴x=0.5.
故选:C.
14.解:根据题意,作△EFC;
3534410248920树高为CD,且∠ECF=90°,ED=8,FD=2;
∵∠E+∠ECD=∠E+∠CFD=90°
∴∠ECD=∠CFD
∴Rt△EDC∽Rt△FDC,
有 EDDC=DCFD;即DC2=ED?FD,
代入数据可得DC2=16,
DC=4;
故选:B.
405066524511015.解:如图当最上层的小长方形的一边与AB、AC交于点E、F时,
EF∥BC,
∴△AEF∽△ABC,
∴EFBC=AGAD
∵BC=12cm,AD=9cm,小正方形邻边长分别为4cm和2cm
∴412=AG9
解得:AG=3,
∴GD=6cm,
∵小正方形的宽为2cm,
∴能分割三层小长方形,
∵BC=12cm,
∴最底层能裁两个小长方形,
故共裁4个小长方形.
故选:B.
16.解:∵由题意得:AE∥BD,
∴CBAB=CDED,CD=CE﹣ED=8.7﹣2.7=6,
∴CB=AB?CDED=1.8×62.7=4m,
∴BC=4m.
故选:C.
17.解:如图,设AD交PN于点K.
∵PM:PQ=3:2,
∴可以假设MP=3k,PQ=2k.
373761096520∵四边形PQNM是矩形,
∴PM∥BC,
∴△APM∽△ABC,
∵AD⊥BC,BC∥PM,
∴AD⊥PM,
∴PMBC=AKAD,
∴3k120=80-2k80,
解得k=20mm,
∴PM=3k=60mm,
故选:A.
18.解:∵AB∥CD,
∴△OAB∽△OCD,
∴OAOC=ABCD,
∴44+3=0.8CD,
解得:CD=1.4(米).
故答案为:1.4.
19.解:如图;AM、BN都与水平线的垂直,M,N是垂足,则AM∥BN;
∵AM∥BN,
352361524130∴△ACM∽△BCN;
∴ACBC=AMBN,
∵AC与BC之比为6:1,
∴ACBC=AMBN=6,即AM=6BN,
∴当BN≥10cm时,AM≥60cm,
故要使这块石头滚动,至少要将杠杆的端点A向下压60cm.
故答案为:60.
20.解:∵BC∥DE,
∴△ABC∽△ADE,
∴BCDE=ABAD,
即2540=ABAB+12,
∴AB=20.
答:河的宽度AB为20米.
21.解:由已知得,AB=1m,CD=1.5m,AC=4m,FB=GD=1.5m,∠AOE=∠ABF=∠CDG=90°,∠BAF=∠OAE,∠DCG=∠OCE.
∵∠BAF=∠OAE,∠ABF=∠AOE,
∴△BAF∽△OAE,
∴FBAB=OEOA,即1.51=OEOA,
∴OE=1.5OA,
∵∠DCG=∠OCE,∠CDG=∠COE,
∴△GDC∽△EOC,
∴GDCD=OEOC,即1.51.5=OEOA+4,
∴OE=OA+4,
∴OE=1.5OA,
339661550165∴1.5OA=OA+4,
∴OA=8m,OE=12m.
答:教学楼的高度OE为12m.
22.解:过E作EF⊥BC于F,
∵∠CDE=135°,
∴∠EDF=45°,
设EF为x米,DF=x米,DE=2x米,
∵∠B=∠EFC=90°,
∵∠ACB=∠ECD,
∴△ABC∽△EFC,
295338545085∴ABEF=BCFC,
即1.5x=624+x,
解得:x=8,
∴DE=82,
答:DE的长度为82米.
23.解:当所截的正方形的边在△ABC的直角边上,如图1,设正方形CDEF边长为x,则DE=xcm,BD=BC﹣CD=(6﹣x)cm,
∵DE∥AC,
∴△BDE∽△BCA,
∴DEAC=BDBC,即x8=6-x6,
解得:x=247(cm),
即正方形BDEF边长为247cm;
当所截的正方形的边在△ABC的斜边上,如图2,作CH⊥AB于H,交MQ于J,
则MN∥CH,
AB=AC2+BC2=82+62=10,
∵12CH?AB=12AC?BC
∴CH=8×610=245(cm),
设正方形MNPQ边长为x,则QM=x,CJ=245-x,
∵QM∥AB,
4366260105410∴△CMQ∽△CBA,
∴QMAB=CJCH,即x10=245-x245,
解得:x=12037(cm),
即正方形BDEF边长为12037(cm);
∵247=12035>12037,
∴图1利用率高.
27.2.3 相似三角形应用举例
基础知识精炼
模块一
基础知识精炼
模块一
【知识点1】利用相似三角形测量物体的高度
【知识点1】利用相似三角形测量物体的高度
1.某数学兴趣小组来到城关区时代广场,设计用手电来测量广场附近某大厦CD的高度,如图,点P处放一水平的平面镜.光线从点A出发经平面镜反射后刚好射到大厦CD的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=1.5米,BP=2米,PD=52米,那么该大厦的高度约为( )
A.39米 B.30米 C.24米 D.15米
2.如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高为1.5m,测得AB=3m,BC=7m,则建筑物CD的高是( )
A.3.5m B.4m C.4.5m D.5m
3.高4米的旗杆在水平地面上的影长为6米,此时测得附近一个建筑物的影长24米,则该建筑物的高度为( )
A.10米 B.16米 C.26米 D.36米
4.如图,为了测量旗杆的高度,某综合实践小组设计了以下方案:用2.5m长的竹竿做测量工具,移动竹竿,保持竹竿与旗杆平行,使竹竿、旗杆的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距5m、与旗杆相距20m,则旗杆的高度为 m.
【知识点2】利用相似三角形测量平面内两点的距离
角形相似
【知识点2】利用相似三角形测量平面内两点的距离
角形相似
5.如图,A,B两点被一河隔开,为了测量A,B两点间的距离,小明过点B作BF⊥AB,在BF上取两点C,D,使BC=2CD,过点D作DE⊥BF且使点A,C,E在同一条直线上,测得DE=20m,则A,B两点间的距离是( )
A.60m B.50m C.40m D.30m
6.我国古代数学著作中记载了一个问题:“今有邑方不知大小,各开中门,出北门四十步有木,出西门八百一十步见木,问:邑方几何?”其大意是:一座正方形城池,西、北边正中各开一道门,从北门往正北方向走40步后刚好有一树木,若从西门往正西方向走810步后正好看到树木,则正方形城池的边长为( )步.
A.360 B.270 C.180 D.90
7.如图,A、B两地之间有一池塘,要测量A、B两地之间的距离.选择一点O,连接AO并延长到点C,使OC=12AO,连接BO并延长到点D,使OD=12BO.测得C、D间距离为30米,则A、B两地之间的距离为( )
A.30米 B.45米 C.60米 D.90米
8.如图,为测量某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=10m,EC=5m,CD=8m,则河的宽度AB长为 m.
【知识点3】相似三角形在实际生活中的其他应用
角形相似
【知识点3】相似三角形在实际生活中的其他应用
角形相似
9.如图,已知零件的外径25mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB,若OC:AC=1:3,量的CD=10mm,则零件的厚度为( )
A.2mm B.2.5mm C.3mm D.3.5mm
10.如图,有一块锐角三角形材料,边BC=120mm,高AD=90mm,要把它加工成矩形零件,使其一边在BC上,其余两个顶点分别在AB,AC,且EH=2EF,则这个矩形零件的长为( )
A.36mm B.80mm C.40mm D.72mm
11.我国古代数学《九章算术》中,有个“井深几何”问题:今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸(1尺=10寸),问井深几何?其意思如图所示,则井深BD的长为( )
A.12尺 B.56尺5寸 C.57尺5寸 D.62尺5寸
12.如图,测量小玻璃管口径的量具ABC,AB的长为12cm,AC被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(DE∥AB),那么小玻璃管口径DE是( )
A.8cm B.10cm C.20cm D.60cm
13.如图,铁道口的栏杆短臂OA长1.2m,长臂OB长19.2m.当长臂外端B升高8m时,短臂外端A下降
( )
A.1.1m B.1m C.0.5m D.0.4m
综合能力提升
模块二
综合能力提升
模块二
14.如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为( )m.
A.2 B.4 C.6 D.8
459295565722515.有一块锐角三角形余料ABC,它的边BC=12cm,BC边上的高为9cm,现要把它分割成若干个邻边长分别为4cm和2cm的小长方形零件,分割方式如图所示(分割线的耗料不计),使最底层的小方形的长为4cm的边在BC上,则按如图方式分割成的小长方形零件最多有( )
A.3个 B.4个
C.5个 D.6个
16.阳光通过窗口照到室内在地上留下ED=2.7m宽的亮区(如图),已知亮区一边到窗下的墙角的距离CE=8.7m,窗口高AB=1.8m,那么窗口底边离地面的高BC等于( )
A.1m B.2m C.4m D.6m
17.如图,有一块三角形余料ABC,BC=120mm,高线AD=80mm,要把它加工成一个矩形零件,使矩形的一边在BC上,点P,M分别在AB,AC上,若满足PM:PQ=3:2,则PM的长为( )
A.60mm B.16013mm C.20mm D.24013mm
18.如图,网高AB为0.8米,击球点到网的水平距离AC为3米,小明在打网球时,要使球恰好能打过网,且落点恰好在离网水平距离OA为4米,则球拍击球的高度CD为 米.
19.如图是用杠杆撬石头的示意图,C是支点,当用力压杠杆的A端时,杠杆绕C点转动,另一端B向上翘起,石头就被撬动.现有一块石头,要使其滚动,杠杆的B端必须向上翘起10cm,已知杠杆的动力臂AC与阻力臂BC之比为6:1,要使这块石头滚动,至少要将杠杆的A端向下压 cm.
20.为了估计河的宽度,勘测人员在河的对岸选定一个目标点A,在近岸分别取点B、D、E、C,使点A、B、D在一条直线上,且AD⊥DE,点A、C、E也在一条直线上,且DE∥BC.经测量BC=25米,BD=12米,DE=40米,求河的宽度AB为多少米?
21.如图,小明同学为了测量教学楼的高度OE,先在操场上点A处放一面镜子,从点A处后退1m到点B处,恰好在镜子中看到楼的顶部E点;再将镜子向后移动4m放在C处,从点C处向后退1.5m到点D处,恰好再次在镜子中看到楼的顶部E点,测得小明的眼睛距地面的高度FB,GD为1.5m,点O,A,B,C,D在同一水平线上,镜子可看成一个点.求教学楼的高度OE.
22.如图,小华和同伴春游时,发现在某地小山坡的点E处有一棵小桃树,他们想利用皮尺、测倾器和平面镜测量小桃树到山脚下的距离(即DE的长度),小华站在点B处,让同伴移动平面镜至点C处,此时小华在平面镜内可以看到点E,且测得BC=6米,CD=24米,∠CDE=135°.已知小华的身高AB=1.5米,请根据以上数据,求DE的长度(结果保留根号)
23.△ABC是一块直角三角形余料,∠C=90°,AC=8cm,BC=6cm,如图将它加工成正方形零件,试说明哪种方法利用率高?(得到的正方形的面积较大)
参考答案与试题解析
1.解:根据题意,得到:△ABP∽△PDC.
即CDAB=PDBP,
故CD=PDBP×AB=522×1.5=39米;
那么该大厦的高度是39米.
故选:A.
2.解:∵EB⊥AC,DC⊥AC,
∴EB∥DC,
∴△ABE∽△ACD,
∴ABAC=BECD,
∵BE=1.5m,AB=3m,BC=7m,
∴AC=AB+BC=10m,
∴310=1.5DC,
解得,DC=5,
即建筑物CD的高是5m,
故选:D.
3.解:设建筑物的高是x米.则x24=46,
解得:x=16.
故该建筑物的高为16米.
故选:B.
4.解:由图可知:
设旗杆的高度为x米,
竹竿高竹竿影长=旗杆高旗杆影长,
2.55=x5+20
解得x=12.5.
故答案为12.5.
5.解:∵AB⊥BF,ED⊥BF,
∴AB∥DE,
∴△ABC∽△EDC,
∴ABDE=BCCD,
即AB20=21,
解得:AB=40,
故选:C.
6.解:如图,设正方形城池的边长为x步,则AE=CE=12x,
3211830174625∵AE∥CD,
∴∠BEA=∠EDC,
∴Rt△BEA∽Rt△EDC,
∴ABEC=AECD,即4012x=12x810,
∴x=360,
即正方形城池的边长为360步.
故选:A.
7.解:∵△ABO和△COD中,OCOA=ODOB=12,
且∠AOB=∠COD,
∴△AOB∽△COD,
∴ABCD=2,
又∵CD=30m,
∴AB=60m.
故选:C.
8.解:∵AB⊥BC,CD⊥BC,
∴∠ABE=∠DCE=90°,
又∵∠AEB=∠DEC(对顶角相等),
∴△ABE∽△DCE,
∴ABCD=BECE,
即AB8=105,
解得AB=16m.
故答案为:16.
9.解:∵两条尺长AC和BD相等,OC=OD,
∴OA=OB,
∵OC:AC=1:3,
∴OC:OA=1:2,
∴OD:OB=OC:OA=1:2,
∵∠COD=∠AOB,
∴△AOB∽△COD,
∴CD:AB=OC:OA=1:2,
∵CD=10mm,
∴AB=20(mm),
∴2x+20=25,
∴x=2.5(mm),
故选:B.
10.解:设边宽为xmm,则长为2xmm,
∵四边形EFGH为矩形,
∴EH∥BC,EF∥AD,
∴EFAD=BEBA,EHBC=AEAB,
∵BE+AE=AB,
∴x90=BEAB,2x120=AEAB,
∴x90+2x120=1,
解得:x=36mm,
∴EF=36mm,EH=72mm,
故选:D.
11.解:∵BC∥DE,
∴△ABC∽△ADE,
3769995-15875∴AB:AD=BC:DE,
即5:AD=0.4:5,
解得AD=62.5,
BD=AD﹣AB=62.5﹣5=57.5尺.
故选:C.
12.解:∵DE∥AB
∴CD:AC=DE:AB
∴40:60=DE:12
∴DE=8cm
故选:A.
13.解:设短臂外端A下降x米,
则8x=19.21.2,
∴x=0.5.
故选:C.
14.解:根据题意,作△EFC;
3534410248920树高为CD,且∠ECF=90°,ED=8,FD=2;
∵∠E+∠ECD=∠E+∠CFD=90°
∴∠ECD=∠CFD
∴Rt△EDC∽Rt△FDC,
有 EDDC=DCFD;即DC2=ED?FD,
代入数据可得DC2=16,
DC=4;
故选:B.
405066524511015.解:如图当最上层的小长方形的一边与AB、AC交于点E、F时,
EF∥BC,
∴△AEF∽△ABC,
∴EFBC=AGAD
∵BC=12cm,AD=9cm,小正方形邻边长分别为4cm和2cm
∴412=AG9
解得:AG=3,
∴GD=6cm,
∵小正方形的宽为2cm,
∴能分割三层小长方形,
∵BC=12cm,
∴最底层能裁两个小长方形,
故共裁4个小长方形.
故选:B.
16.解:∵由题意得:AE∥BD,
∴CBAB=CDED,CD=CE﹣ED=8.7﹣2.7=6,
∴CB=AB?CDED=1.8×62.7=4m,
∴BC=4m.
故选:C.
17.解:如图,设AD交PN于点K.
∵PM:PQ=3:2,
∴可以假设MP=3k,PQ=2k.
373761096520∵四边形PQNM是矩形,
∴PM∥BC,
∴△APM∽△ABC,
∵AD⊥BC,BC∥PM,
∴AD⊥PM,
∴PMBC=AKAD,
∴3k120=80-2k80,
解得k=20mm,
∴PM=3k=60mm,
故选:A.
18.解:∵AB∥CD,
∴△OAB∽△OCD,
∴OAOC=ABCD,
∴44+3=0.8CD,
解得:CD=1.4(米).
故答案为:1.4.
19.解:如图;AM、BN都与水平线的垂直,M,N是垂足,则AM∥BN;
∵AM∥BN,
352361524130∴△ACM∽△BCN;
∴ACBC=AMBN,
∵AC与BC之比为6:1,
∴ACBC=AMBN=6,即AM=6BN,
∴当BN≥10cm时,AM≥60cm,
故要使这块石头滚动,至少要将杠杆的端点A向下压60cm.
故答案为:60.
20.解:∵BC∥DE,
∴△ABC∽△ADE,
∴BCDE=ABAD,
即2540=ABAB+12,
∴AB=20.
答:河的宽度AB为20米.
21.解:由已知得,AB=1m,CD=1.5m,AC=4m,FB=GD=1.5m,∠AOE=∠ABF=∠CDG=90°,∠BAF=∠OAE,∠DCG=∠OCE.
∵∠BAF=∠OAE,∠ABF=∠AOE,
∴△BAF∽△OAE,
∴FBAB=OEOA,即1.51=OEOA,
∴OE=1.5OA,
∵∠DCG=∠OCE,∠CDG=∠COE,
∴△GDC∽△EOC,
∴GDCD=OEOC,即1.51.5=OEOA+4,
∴OE=OA+4,
∴OE=1.5OA,
339661550165∴1.5OA=OA+4,
∴OA=8m,OE=12m.
答:教学楼的高度OE为12m.
22.解:过E作EF⊥BC于F,
∵∠CDE=135°,
∴∠EDF=45°,
设EF为x米,DF=x米,DE=2x米,
∵∠B=∠EFC=90°,
∵∠ACB=∠ECD,
∴△ABC∽△EFC,
295338545085∴ABEF=BCFC,
即1.5x=624+x,
解得:x=8,
∴DE=82,
答:DE的长度为82米.
23.解:当所截的正方形的边在△ABC的直角边上,如图1,设正方形CDEF边长为x,则DE=xcm,BD=BC﹣CD=(6﹣x)cm,
∵DE∥AC,
∴△BDE∽△BCA,
∴DEAC=BDBC,即x8=6-x6,
解得:x=247(cm),
即正方形BDEF边长为247cm;
当所截的正方形的边在△ABC的斜边上,如图2,作CH⊥AB于H,交MQ于J,
则MN∥CH,
AB=AC2+BC2=82+62=10,
∵12CH?AB=12AC?BC
∴CH=8×610=245(cm),
设正方形MNPQ边长为x,则QM=x,CJ=245-x,
∵QM∥AB,
4366260105410∴△CMQ∽△CBA,
∴QMAB=CJCH,即x10=245-x245,
解得:x=12037(cm),
即正方形BDEF边长为12037(cm);
∵247=12035>12037,
∴图1利用率高.
