2020-2021学年上海市浦东新区第四教育署八年级上学期期末数学试卷(五四学制) (Word版 含解析)
文档属性
| 名称 | 2020-2021学年上海市浦东新区第四教育署八年级上学期期末数学试卷(五四学制) (Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 658.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-06 05:32:33 | ||
图片预览




文档简介
2020-2021学年上海市浦东新区第四教育署八年级第一学期期末数学试卷
一、单项选择题(共6小题).
1.在下列式子中,表示y是x的正比例函数的是( )
A.y= B.y=x2 C.y= D.y=
2.在下列方程中,有两个不相等实数根的是( )
A.x2=2x﹣4 B.x2﹣4x+4=0 C.x2﹣2x﹣1=0 D.x2+4=0
3.下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
4.若正比例函数y=(2﹣k)x的图象经过第二、四象限,则k的取值范围是( )
A.k<﹣2 B.k<2 C.k>﹣2 D.k>2
5.下列命题的逆命题是真命题的是( )
A.若a=b,则|a|=|b|
B.同位角相等,两直线平行
C.对顶角相等
D.若a>0,b>0,则a+b>0
6.在下列四个条件:①AB2+BC2=AC2,②∠A=90°﹣∠B,③∠A=∠B=∠C,④∠A:∠B:∠C=5:3:2中,能确定△ABC是直角三角形的条件有( )
A.①③ B.①②③ C.①②④ D.①②③④
二、填空题(共12小题).
7.若有意义,那么x满足的条件是 .
8.计算:()2+1= .
9.方程x2=x的解是 .
10.如果函数y=(m﹣)x是正比例函数,那么m= .
11.如果反比例函数y=(k≠0)的图象经过点P(5,﹣2),那么在这个函数图象所在的每个象限内,y的值随x的值增大而 .(填“增大”或“减小”)
12.某商店今年7月份的销售额是50万元,9月份的销售额是72万元,从7月份到9月份,该店销售额平均每月的增长率是 .
13.平面内到点O的距离等于3厘米的点的轨迹是 .
14.在直角三角形中,两直角边分别为6和8,则第三边上中线长是 .
15.已知点A(3,3),B(0,t),C(7,0),且AB=AC,则t= .
16.如图,DF垂直平分AB,EG垂直平分AC,若∠BAC=110°,则∠DAE= °.
17.如图所示,在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,BD平分∠ABC,DE⊥AB,垂足为E,则DE= cm.
18.如图,点P(a,a)是反比例函数在第一象限内的图象上的一个点,以点P为顶点作等边△PAB,使A、B落在x轴上(点A在点B左侧),则△POA的面积是 .
三、简答题(本大题共7小题,第19、20题每题5分,第21、22题每题6分,第23题8分,第24题10分,第25题12分,共52分)
19..
20.解方程:2x2+4x﹣7=0.
21.已知y与x+1成反比例,且当x=1时,y=2,求当x=0时,y的值.
22.如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,AD=20,求BC的长.
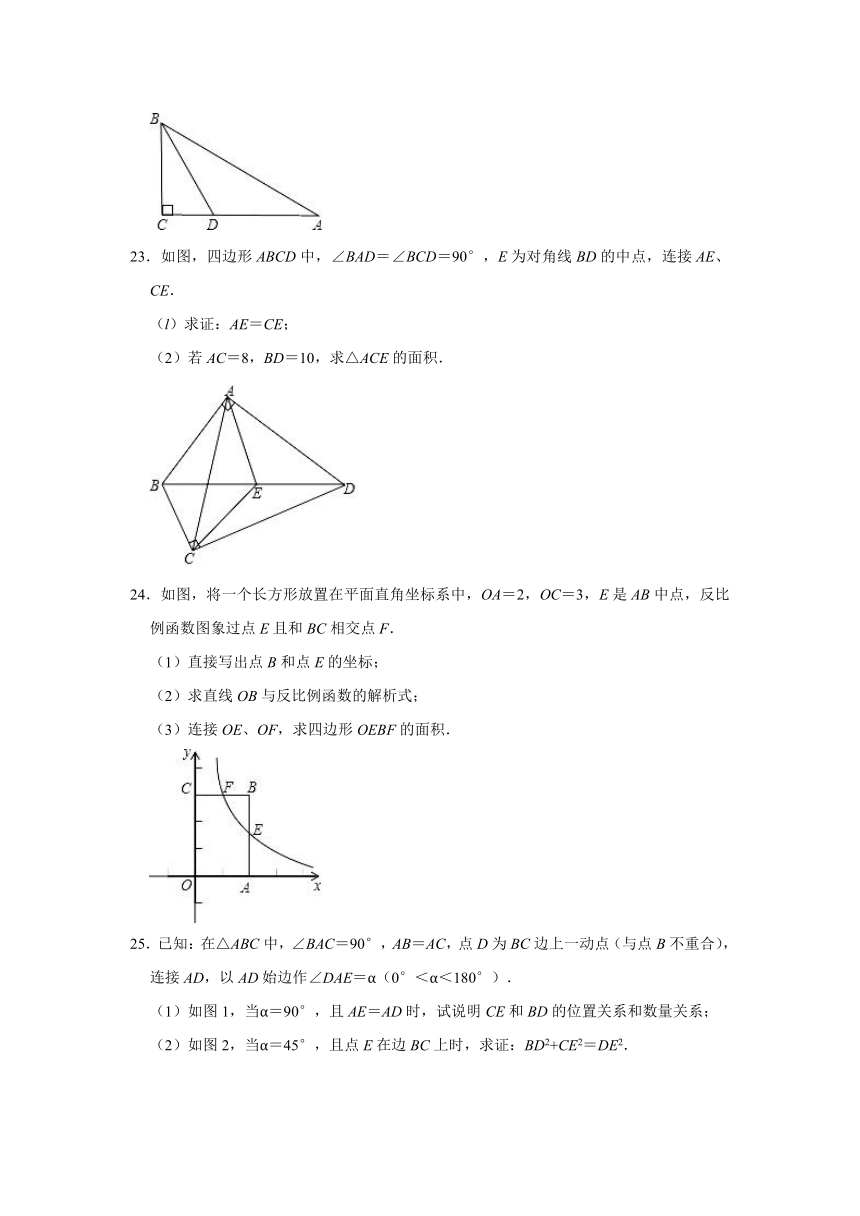
23.如图,四边形ABCD中,∠BAD=∠BCD=90°,E为对角线BD的中点,连接AE、CE.
(l)求证:AE=CE;
(2)若AC=8,BD=10,求△ACE的面积.
24.如图,将一个长方形放置在平面直角坐标系中,OA=2,OC=3,E是AB中点,反比例函数图象过点E且和BC相交点F.
(1)直接写出点B和点E的坐标;
(2)求直线OB与反比例函数的解析式;
(3)连接OE、OF,求四边形OEBF的面积.
25.已知:在△ABC中,∠BAC=90°,AB=AC,点D为BC边上一动点(与点B不重合),连接AD,以AD始边作∠DAE=α(0°<α<180°).
(1)如图1,当α=90°,且AE=AD时,试说明CE和BD的位置关系和数量关系;
(2)如图2,当α=45°,且点E在边BC上时,求证:BD2+CE2=DE2.
参考答案
一、单项选择题(本大题共有6题,每题2分,共12分)
1.在下列式子中,表示y是x的正比例函数的是( )
A.y= B.y=x2 C.y= D.y=
【分析】根据正比例函数的定义进行判断即可.
解:根据正比例函数的定义可得,形如y=kx(k≠0),y是x的正比例函数,
由于y==x,因此y=是自变量函数,
故选:C.
2.在下列方程中,有两个不相等实数根的是( )
A.x2=2x﹣4 B.x2﹣4x+4=0 C.x2﹣2x﹣1=0 D.x2+4=0
【分析】先计算各方程的根的判别式,然后根据判别式的意义判断方程根的情况,从而得到正确答案.
解:A、方程化为x2﹣2x+4=0,则△=(﹣2)2﹣4×4=﹣12<0,方程无实数根,所以A选项不符合题意;
B、△=(﹣4)2﹣4×4=0,方程有两个相等的实数根,所以B选项不符合题意;
C、△=(﹣2)2﹣4×(﹣1)=8>0,方程有两个不相等的实数根,所以C选项符合题意;
D、△=02﹣4×4=﹣16<0,方程无实数根,所以D选项不符合题意.
故选:C.
3.下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
【分析】先将各选项化简,再根据同类二次根式的定义解答.
解:A、与被开方数相同,故是同类二次根式;
B、与被开方数不相同,故不是同类二次根式;
C、与被开方数不相同,故不是同类二次根式;
D、与被开方数不相同,故不是同类二次根式;
故选:A.
4.若正比例函数y=(2﹣k)x的图象经过第二、四象限,则k的取值范围是( )
A.k<﹣2 B.k<2 C.k>﹣2 D.k>2
【分析】根据正比例函数的性质和已知得出关于k的不等式,求出不等式的解集即可.
解:∵正比例函数y=(2﹣k)x的图象经过第二、四象限,
∴2﹣k<0,
解得:k>2,
故选:D.
5.下列命题的逆命题是真命题的是( )
A.若a=b,则|a|=|b|
B.同位角相等,两直线平行
C.对顶角相等
D.若a>0,b>0,则a+b>0
【分析】分别写出原命题的逆命题,然后判断真假即可.
解:A、若a=b,则|a|=|b|的逆命题是若|a|=|b|,则a=b,逆命题是假命题,不符合题意;
B、同位角相等,两直线平行的逆命题是两直线平行,同位角相等,逆命题是真命题,符合题意;
C、对顶角相等的逆命题是相等的角是对顶角,逆命题是假命题,不符合题意;
D、若a>0,b>0,则a+b>0的逆命题是若a+b>0,则a>0,b>0,逆命题是假命题,不符合题意;
故选:B.
6.在下列四个条件:①AB2+BC2=AC2,②∠A=90°﹣∠B,③∠A=∠B=∠C,④∠A:∠B:∠C=5:3:2中,能确定△ABC是直角三角形的条件有( )
A.①③ B.①②③ C.①②④ D.①②③④
【分析】根据直角三角形的判定对各个条件进行分析,即可得到答案.
解:①∵AB2+BC2=AC2,
∴∠B=90°,
∴△ABC是直角三角形;
②∵∠A=90°﹣∠B,
∴∠A+∠B=90°,
∴∠C=90°,
∴△ABC是直角三角形;
③∵∠A=∠B=∠C,
∴∠C=180°=90°,
∴△ABC是直角三角形;
④∵∠A:∠B:∠C=5:3:2,
∴∠A=180°×=90°,
∴△ABC为直角三角形.
∴能确定△ABC是直角三角形的有①②③④共4个,
故选:D.
二、填空题(本大题共有12小题,每题3分,共36分)
7.若有意义,那么x满足的条件是 x≤1 .
【分析】根据二次根式有意义的条件列出不等式,解不等式得到答案.
解:要使有意义,则1﹣x≥0,
解得,x≤1,
故答案为:x≤1.
8.计算:()2+1= 4 .
【分析】先乘方,再加法.
解:原式=3+1=4.
故答案为:4.
9.方程x2=x的解是 x1=0,x2=1 .
【分析】将方程化为一般形式,提取公因式分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程,求出一次方程的解即可得到原方程的解.
解:x2=x,
移项得:x2﹣x=0,
分解因式得:x(x﹣1)=0,
可得x=0或x﹣1=0,
解得:x1=0,x2=1.
故答案为:x1=0,x2=1
10.如果函数y=(m﹣)x是正比例函数,那么m= ﹣ .
【分析】根据正比例函数的定义得出m﹣0且m2﹣1=1,再求出即可.
解:∵函数y=(m﹣)x是正比例函数,
∴m﹣0且m2﹣1=1,
解得:m=﹣,
故答案为:﹣.
11.如果反比例函数y=(k≠0)的图象经过点P(5,﹣2),那么在这个函数图象所在的每个象限内,y的值随x的值增大而 增大 .(填“增大”或“减小”)
【分析】先根据反比例函数图象上点的坐标特征求出k的值,然后根据反比例函数的性质进行判断.
解:∵反比例函数y=(k≠0)的图象经过点P(5,﹣2),
∴k=5×(﹣2)=﹣10,
∵k<0,
∴反比例函数图象分布在第二、四象限,在每个象限内,y的值随x的值增大而增大.
故答案为增大.
12.某商店今年7月份的销售额是50万元,9月份的销售额是72万元,从7月份到9月份,该店销售额平均每月的增长率是 20% .
【分析】设该店销售额平均每月的增长率是x,根据该商店今年7月份及9月份的销售额,即可得出关于x的一元二次方程,解之取其正值即可得出结论.
解:设该店销售额平均每月的增长率是x,
依题意得:50(1+x)2=72,
解得:x1=0.2=20%,x2=﹣2.2(不合题意,舍去).
故答案为:20%.
13.平面内到点O的距离等于3厘米的点的轨迹是 以点O为圆心,3厘米长为半径的圆 .
【分析】只需根据圆的定义就可解决问题.
解:平面内到点O的距离等于3厘米的点的轨迹是以点O为圆心,3厘米长为半径的圆.
故答案为:以点O为圆心,3厘米长为半径的圆.
14.在直角三角形中,两直角边分别为6和8,则第三边上中线长是 5 .
【分析】已知直角三角形的两条直角边,根据勾股定理即可求斜边的长度,根据斜边中线长为斜边长的一半即可解题.
解:已知直角三角形的两直角边为6、8,
则斜边长为=10,
故斜边的中线长为×10=5,
故答案是:5.
15.已知点A(3,3),B(0,t),C(7,0),且AB=AC,则t= 7或﹣1 .
【分析】利用勾股定理求得AB、AC的长度,然后结合已知条件AB=AC列出关于t的方程,解方程即可.
解:依题意,得=.
解得t=7或t=﹣1.
故答案是:7或﹣1.
16.如图,DF垂直平分AB,EG垂直平分AC,若∠BAC=110°,则∠DAE= 40 °.
【分析】根据三角形内角和定理得到∠B+∠C=70°,根据线段垂直平分线的性质得到DA=DB,EA=EC,根据等腰三角形的性质计算,得到答案.
解:∵∠BAC=110°,
∴∠B+∠C=180°﹣∠BAC=180°﹣110°=70°,
∵DF垂直平分AB,EG垂直平分AC,
∴DA=DB,EA=EC,
∴∠DAB=∠B,∠EAC=∠C,
∴∠DAB+∠EAC=∠B+∠C=70°,
∴∠DAE=∠BAC﹣(∠DAB+∠EAC)=40°,
故答案为:40.
17.如图所示,在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,BD平分∠ABC,DE⊥AB,垂足为E,则DE= cm.
【分析】首先根据勾股定理求得AC=6cm;然后利用角平分线的性质求得ED=CD,设ED=CD=x;最后在直角△ACD中,利用勾股定理列出方程,解方程即可.
解:如图所示,在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,则由勾股定理得到:AC===6(cm).
∵BD平分∠ABC,DE⊥AB,CD⊥BC,
∴ED=CD,设ED=CD=x(x>0),
在直角△ACD中,AD2=AE2+ED2,即(6﹣x)2=(10﹣8)2+x2.
解得x=.
即DE=cm.
故答案是:.
18.如图,点P(a,a)是反比例函数在第一象限内的图象上的一个点,以点P为顶点作等边△PAB,使A、B落在x轴上(点A在点B左侧),则△POA的面积是 8﹣ .
【分析】如图,根据反比例函数系数k的几何意义求得点P的坐标,则易求PD=4.然后通过等边三角形的性质易求线段AD=,所以S△POA=OA?PD=××4=8﹣
解:如图,∵点P(a,a)是反比例函数在第一象限内的图象上的一个点,
∴16=a2,且a>0,
解得,a=4,
∴PD=4.
∵△PAB是等边三角形,
∴AD=.
∴OA=4﹣AD=,
∴S△POA=OA?PD=××4=8﹣.
故答案是:.
三、简答题(本大题共7小题,第19、20题每题5分,第21、22题每题6分,第23题8分,第24题10分,第25题12分,共52分)
19..
【分析】利用二次根式的乘除法则和二次根式的性质计算.
解:原式=﹣﹣2
=2﹣﹣2
=﹣2.
20.解方程:2x2+4x﹣7=0.
【分析】根据配方法的步骤依次计算可得.
解:2x2+4x﹣7=0,
2x2+4x=7,
x2+2x=,
x2+2x+1=+1,即(x+1)2=,
∴x+1=±,
∴x1=,x2=.
21.已知y与x+1成反比例,且当x=1时,y=2,求当x=0时,y的值.
【分析】利用y与x+1成反比例设y=(k≠0),再把x=1,y=2代入求出k得到y=,然后计算自变量为0所对应的函数值.
解:根据题意得,设y=(k≠0),
∵x=1,y=2,
∴2=,
∴k=4,
∴y=,
当x=0时,y==4.
22.如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,AD=20,求BC的长.
【分析】先求出∠ABC=60°,再求出∠CBD=∠ABD=30°,得出∠ABD=∠A,求出BD,再求出CD,最后根据BC=代入计算即可.
解:∵∠C=90°,∠A=30°,
∴∠ABC=60°,
∵BD是∠ABC的平分线,
∴∠CBD=∠ABD=30°,
∴∠ABD=∠A,
∴AD=BD=20,
∴CD=BD=10,
∴BC===10.
23.如图,四边形ABCD中,∠BAD=∠BCD=90°,E为对角线BD的中点,连接AE、CE.
(l)求证:AE=CE;
(2)若AC=8,BD=10,求△ACE的面积.
【分析】(1)根据直角三角形斜边上的中线等于斜边的一半推知AE=CE=BD;
(2)如图,过点E作EG⊥AC,根据等腰△AEC的性质和勾股定理求得EG的长度,然后结合三角形的面积公式解答即可.
【解答】(1)证明:∵∠BAD=∠BCD=90°,E为对角线BD的中点,
∴AE=BD,CE=BD,
∴AE=CE;
(2)解:如图,过点E作EG⊥AC,
由(1)知,AE=CE=BD,BD=10,
∴AE=CE=5.
又∵EG⊥AC,
∴AG=CG=AC.
又∵AC=8,
∴AG=CG=4.
在直角△ABE中,AE=5,AG=4,则由勾股定理知:EG==3.
∴S==12.
24.如图,将一个长方形放置在平面直角坐标系中,OA=2,OC=3,E是AB中点,反比例函数图象过点E且和BC相交点F.
(1)直接写出点B和点E的坐标;
(2)求直线OB与反比例函数的解析式;
(3)连接OE、OF,求四边形OEBF的面积.
【分析】(1)根据OA=2,OC=3,得到点B的坐标;
(2)运用待定系数法求直线OB的解析式,根据E是AB的中点,求得点E的坐标,再进一步运用待定系数法求得反比例函数的解析式;
(3)根据反比例函数的解析式求得点F的横坐标,再进一步根据四边形的面积等于矩形的面积减去两个直角三角形的面积进行计算.
解:(1)∵OA=2,OC=3,E是AB中点,
∴B(2,3),E(2,);
(2)设直线OB的解析式是y=k1x,
把B点坐标代入,得k1=,
则直线OB的解析式是y=x.
设反比例函数解析式是y=,
把E点坐标代入,得k2=3,
则反比例函数的解析式是y=;
(2)由题意得Fy=3,代入,
得Fx=1,即F(1,3).
则四边形OEBF的面积=矩形OABC的面积﹣△OAE的面积﹣△OCF的面积=2×3﹣1×3﹣2×=3.
25.已知:在△ABC中,∠BAC=90°,AB=AC,点D为BC边上一动点(与点B不重合),连接AD,以AD始边作∠DAE=α(0°<α<180°).
(1)如图1,当α=90°,且AE=AD时,试说明CE和BD的位置关系和数量关系;
(2)如图2,当α=45°,且点E在边BC上时,求证:BD2+CE2=DE2.
【分析】(1)根据∠BAD=∠CAE,BA=CA,AD=AE,运用“SAS”证明△ABD≌△ACE,根据全等三角形性质得出对应边相等,对应角相等,即可得到线段CE、BD之间的关系;
(2)把△ACE绕点A顺时针旋转90°,得到△ABG.连接DG,由“SAS”得到△ADG≌△ADE,可得DE=DG,即可把EF,BE,FC放到一个直角三角形中,从而根据勾股定理即可证明;
解:(1)CE与BD位置关系是CE⊥BD,数量关系是CE=BD.
理由:∵∠BAC=∠DAE=90°,
∴∠BAD=90°﹣∠DAC,∠CAE=90°﹣∠DAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE (SAS),
∴∠ACE=∠B=45°且 CE=BD.
∵∠ACB=∠B=45°,
∴∠ECB=45°+45°=90°,即CE⊥BD;
(2)如图2,把△ACE绕点A顺时针旋转90°,得到△ABG.连接DG,
则△ACE≌△ABG,
∴AG=AE,BG=CE,∠ABG=∠ACE=45°.
∵∠BAC=90°,∠GAE=90°.
∴∠GAD=∠DAE=45°,
在△ADG和△ADE中,
,
∴△ADG≌△ADE(SAS).
∴ED=GD,
又∵∠GBD=90°,
∴BD2+BG2=DG2,
即BD2+EC2=DE2;
一、单项选择题(共6小题).
1.在下列式子中,表示y是x的正比例函数的是( )
A.y= B.y=x2 C.y= D.y=
2.在下列方程中,有两个不相等实数根的是( )
A.x2=2x﹣4 B.x2﹣4x+4=0 C.x2﹣2x﹣1=0 D.x2+4=0
3.下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
4.若正比例函数y=(2﹣k)x的图象经过第二、四象限,则k的取值范围是( )
A.k<﹣2 B.k<2 C.k>﹣2 D.k>2
5.下列命题的逆命题是真命题的是( )
A.若a=b,则|a|=|b|
B.同位角相等,两直线平行
C.对顶角相等
D.若a>0,b>0,则a+b>0
6.在下列四个条件:①AB2+BC2=AC2,②∠A=90°﹣∠B,③∠A=∠B=∠C,④∠A:∠B:∠C=5:3:2中,能确定△ABC是直角三角形的条件有( )
A.①③ B.①②③ C.①②④ D.①②③④
二、填空题(共12小题).
7.若有意义,那么x满足的条件是 .
8.计算:()2+1= .
9.方程x2=x的解是 .
10.如果函数y=(m﹣)x是正比例函数,那么m= .
11.如果反比例函数y=(k≠0)的图象经过点P(5,﹣2),那么在这个函数图象所在的每个象限内,y的值随x的值增大而 .(填“增大”或“减小”)
12.某商店今年7月份的销售额是50万元,9月份的销售额是72万元,从7月份到9月份,该店销售额平均每月的增长率是 .
13.平面内到点O的距离等于3厘米的点的轨迹是 .
14.在直角三角形中,两直角边分别为6和8,则第三边上中线长是 .
15.已知点A(3,3),B(0,t),C(7,0),且AB=AC,则t= .
16.如图,DF垂直平分AB,EG垂直平分AC,若∠BAC=110°,则∠DAE= °.
17.如图所示,在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,BD平分∠ABC,DE⊥AB,垂足为E,则DE= cm.
18.如图,点P(a,a)是反比例函数在第一象限内的图象上的一个点,以点P为顶点作等边△PAB,使A、B落在x轴上(点A在点B左侧),则△POA的面积是 .
三、简答题(本大题共7小题,第19、20题每题5分,第21、22题每题6分,第23题8分,第24题10分,第25题12分,共52分)
19..
20.解方程:2x2+4x﹣7=0.
21.已知y与x+1成反比例,且当x=1时,y=2,求当x=0时,y的值.
22.如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,AD=20,求BC的长.
23.如图,四边形ABCD中,∠BAD=∠BCD=90°,E为对角线BD的中点,连接AE、CE.
(l)求证:AE=CE;
(2)若AC=8,BD=10,求△ACE的面积.
24.如图,将一个长方形放置在平面直角坐标系中,OA=2,OC=3,E是AB中点,反比例函数图象过点E且和BC相交点F.
(1)直接写出点B和点E的坐标;
(2)求直线OB与反比例函数的解析式;
(3)连接OE、OF,求四边形OEBF的面积.
25.已知:在△ABC中,∠BAC=90°,AB=AC,点D为BC边上一动点(与点B不重合),连接AD,以AD始边作∠DAE=α(0°<α<180°).
(1)如图1,当α=90°,且AE=AD时,试说明CE和BD的位置关系和数量关系;
(2)如图2,当α=45°,且点E在边BC上时,求证:BD2+CE2=DE2.
参考答案
一、单项选择题(本大题共有6题,每题2分,共12分)
1.在下列式子中,表示y是x的正比例函数的是( )
A.y= B.y=x2 C.y= D.y=
【分析】根据正比例函数的定义进行判断即可.
解:根据正比例函数的定义可得,形如y=kx(k≠0),y是x的正比例函数,
由于y==x,因此y=是自变量函数,
故选:C.
2.在下列方程中,有两个不相等实数根的是( )
A.x2=2x﹣4 B.x2﹣4x+4=0 C.x2﹣2x﹣1=0 D.x2+4=0
【分析】先计算各方程的根的判别式,然后根据判别式的意义判断方程根的情况,从而得到正确答案.
解:A、方程化为x2﹣2x+4=0,则△=(﹣2)2﹣4×4=﹣12<0,方程无实数根,所以A选项不符合题意;
B、△=(﹣4)2﹣4×4=0,方程有两个相等的实数根,所以B选项不符合题意;
C、△=(﹣2)2﹣4×(﹣1)=8>0,方程有两个不相等的实数根,所以C选项符合题意;
D、△=02﹣4×4=﹣16<0,方程无实数根,所以D选项不符合题意.
故选:C.
3.下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
【分析】先将各选项化简,再根据同类二次根式的定义解答.
解:A、与被开方数相同,故是同类二次根式;
B、与被开方数不相同,故不是同类二次根式;
C、与被开方数不相同,故不是同类二次根式;
D、与被开方数不相同,故不是同类二次根式;
故选:A.
4.若正比例函数y=(2﹣k)x的图象经过第二、四象限,则k的取值范围是( )
A.k<﹣2 B.k<2 C.k>﹣2 D.k>2
【分析】根据正比例函数的性质和已知得出关于k的不等式,求出不等式的解集即可.
解:∵正比例函数y=(2﹣k)x的图象经过第二、四象限,
∴2﹣k<0,
解得:k>2,
故选:D.
5.下列命题的逆命题是真命题的是( )
A.若a=b,则|a|=|b|
B.同位角相等,两直线平行
C.对顶角相等
D.若a>0,b>0,则a+b>0
【分析】分别写出原命题的逆命题,然后判断真假即可.
解:A、若a=b,则|a|=|b|的逆命题是若|a|=|b|,则a=b,逆命题是假命题,不符合题意;
B、同位角相等,两直线平行的逆命题是两直线平行,同位角相等,逆命题是真命题,符合题意;
C、对顶角相等的逆命题是相等的角是对顶角,逆命题是假命题,不符合题意;
D、若a>0,b>0,则a+b>0的逆命题是若a+b>0,则a>0,b>0,逆命题是假命题,不符合题意;
故选:B.
6.在下列四个条件:①AB2+BC2=AC2,②∠A=90°﹣∠B,③∠A=∠B=∠C,④∠A:∠B:∠C=5:3:2中,能确定△ABC是直角三角形的条件有( )
A.①③ B.①②③ C.①②④ D.①②③④
【分析】根据直角三角形的判定对各个条件进行分析,即可得到答案.
解:①∵AB2+BC2=AC2,
∴∠B=90°,
∴△ABC是直角三角形;
②∵∠A=90°﹣∠B,
∴∠A+∠B=90°,
∴∠C=90°,
∴△ABC是直角三角形;
③∵∠A=∠B=∠C,
∴∠C=180°=90°,
∴△ABC是直角三角形;
④∵∠A:∠B:∠C=5:3:2,
∴∠A=180°×=90°,
∴△ABC为直角三角形.
∴能确定△ABC是直角三角形的有①②③④共4个,
故选:D.
二、填空题(本大题共有12小题,每题3分,共36分)
7.若有意义,那么x满足的条件是 x≤1 .
【分析】根据二次根式有意义的条件列出不等式,解不等式得到答案.
解:要使有意义,则1﹣x≥0,
解得,x≤1,
故答案为:x≤1.
8.计算:()2+1= 4 .
【分析】先乘方,再加法.
解:原式=3+1=4.
故答案为:4.
9.方程x2=x的解是 x1=0,x2=1 .
【分析】将方程化为一般形式,提取公因式分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程,求出一次方程的解即可得到原方程的解.
解:x2=x,
移项得:x2﹣x=0,
分解因式得:x(x﹣1)=0,
可得x=0或x﹣1=0,
解得:x1=0,x2=1.
故答案为:x1=0,x2=1
10.如果函数y=(m﹣)x是正比例函数,那么m= ﹣ .
【分析】根据正比例函数的定义得出m﹣0且m2﹣1=1,再求出即可.
解:∵函数y=(m﹣)x是正比例函数,
∴m﹣0且m2﹣1=1,
解得:m=﹣,
故答案为:﹣.
11.如果反比例函数y=(k≠0)的图象经过点P(5,﹣2),那么在这个函数图象所在的每个象限内,y的值随x的值增大而 增大 .(填“增大”或“减小”)
【分析】先根据反比例函数图象上点的坐标特征求出k的值,然后根据反比例函数的性质进行判断.
解:∵反比例函数y=(k≠0)的图象经过点P(5,﹣2),
∴k=5×(﹣2)=﹣10,
∵k<0,
∴反比例函数图象分布在第二、四象限,在每个象限内,y的值随x的值增大而增大.
故答案为增大.
12.某商店今年7月份的销售额是50万元,9月份的销售额是72万元,从7月份到9月份,该店销售额平均每月的增长率是 20% .
【分析】设该店销售额平均每月的增长率是x,根据该商店今年7月份及9月份的销售额,即可得出关于x的一元二次方程,解之取其正值即可得出结论.
解:设该店销售额平均每月的增长率是x,
依题意得:50(1+x)2=72,
解得:x1=0.2=20%,x2=﹣2.2(不合题意,舍去).
故答案为:20%.
13.平面内到点O的距离等于3厘米的点的轨迹是 以点O为圆心,3厘米长为半径的圆 .
【分析】只需根据圆的定义就可解决问题.
解:平面内到点O的距离等于3厘米的点的轨迹是以点O为圆心,3厘米长为半径的圆.
故答案为:以点O为圆心,3厘米长为半径的圆.
14.在直角三角形中,两直角边分别为6和8,则第三边上中线长是 5 .
【分析】已知直角三角形的两条直角边,根据勾股定理即可求斜边的长度,根据斜边中线长为斜边长的一半即可解题.
解:已知直角三角形的两直角边为6、8,
则斜边长为=10,
故斜边的中线长为×10=5,
故答案是:5.
15.已知点A(3,3),B(0,t),C(7,0),且AB=AC,则t= 7或﹣1 .
【分析】利用勾股定理求得AB、AC的长度,然后结合已知条件AB=AC列出关于t的方程,解方程即可.
解:依题意,得=.
解得t=7或t=﹣1.
故答案是:7或﹣1.
16.如图,DF垂直平分AB,EG垂直平分AC,若∠BAC=110°,则∠DAE= 40 °.
【分析】根据三角形内角和定理得到∠B+∠C=70°,根据线段垂直平分线的性质得到DA=DB,EA=EC,根据等腰三角形的性质计算,得到答案.
解:∵∠BAC=110°,
∴∠B+∠C=180°﹣∠BAC=180°﹣110°=70°,
∵DF垂直平分AB,EG垂直平分AC,
∴DA=DB,EA=EC,
∴∠DAB=∠B,∠EAC=∠C,
∴∠DAB+∠EAC=∠B+∠C=70°,
∴∠DAE=∠BAC﹣(∠DAB+∠EAC)=40°,
故答案为:40.
17.如图所示,在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,BD平分∠ABC,DE⊥AB,垂足为E,则DE= cm.
【分析】首先根据勾股定理求得AC=6cm;然后利用角平分线的性质求得ED=CD,设ED=CD=x;最后在直角△ACD中,利用勾股定理列出方程,解方程即可.
解:如图所示,在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,则由勾股定理得到:AC===6(cm).
∵BD平分∠ABC,DE⊥AB,CD⊥BC,
∴ED=CD,设ED=CD=x(x>0),
在直角△ACD中,AD2=AE2+ED2,即(6﹣x)2=(10﹣8)2+x2.
解得x=.
即DE=cm.
故答案是:.
18.如图,点P(a,a)是反比例函数在第一象限内的图象上的一个点,以点P为顶点作等边△PAB,使A、B落在x轴上(点A在点B左侧),则△POA的面积是 8﹣ .
【分析】如图,根据反比例函数系数k的几何意义求得点P的坐标,则易求PD=4.然后通过等边三角形的性质易求线段AD=,所以S△POA=OA?PD=××4=8﹣
解:如图,∵点P(a,a)是反比例函数在第一象限内的图象上的一个点,
∴16=a2,且a>0,
解得,a=4,
∴PD=4.
∵△PAB是等边三角形,
∴AD=.
∴OA=4﹣AD=,
∴S△POA=OA?PD=××4=8﹣.
故答案是:.
三、简答题(本大题共7小题,第19、20题每题5分,第21、22题每题6分,第23题8分,第24题10分,第25题12分,共52分)
19..
【分析】利用二次根式的乘除法则和二次根式的性质计算.
解:原式=﹣﹣2
=2﹣﹣2
=﹣2.
20.解方程:2x2+4x﹣7=0.
【分析】根据配方法的步骤依次计算可得.
解:2x2+4x﹣7=0,
2x2+4x=7,
x2+2x=,
x2+2x+1=+1,即(x+1)2=,
∴x+1=±,
∴x1=,x2=.
21.已知y与x+1成反比例,且当x=1时,y=2,求当x=0时,y的值.
【分析】利用y与x+1成反比例设y=(k≠0),再把x=1,y=2代入求出k得到y=,然后计算自变量为0所对应的函数值.
解:根据题意得,设y=(k≠0),
∵x=1,y=2,
∴2=,
∴k=4,
∴y=,
当x=0时,y==4.
22.如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,AD=20,求BC的长.
【分析】先求出∠ABC=60°,再求出∠CBD=∠ABD=30°,得出∠ABD=∠A,求出BD,再求出CD,最后根据BC=代入计算即可.
解:∵∠C=90°,∠A=30°,
∴∠ABC=60°,
∵BD是∠ABC的平分线,
∴∠CBD=∠ABD=30°,
∴∠ABD=∠A,
∴AD=BD=20,
∴CD=BD=10,
∴BC===10.
23.如图,四边形ABCD中,∠BAD=∠BCD=90°,E为对角线BD的中点,连接AE、CE.
(l)求证:AE=CE;
(2)若AC=8,BD=10,求△ACE的面积.
【分析】(1)根据直角三角形斜边上的中线等于斜边的一半推知AE=CE=BD;
(2)如图,过点E作EG⊥AC,根据等腰△AEC的性质和勾股定理求得EG的长度,然后结合三角形的面积公式解答即可.
【解答】(1)证明:∵∠BAD=∠BCD=90°,E为对角线BD的中点,
∴AE=BD,CE=BD,
∴AE=CE;
(2)解:如图,过点E作EG⊥AC,
由(1)知,AE=CE=BD,BD=10,
∴AE=CE=5.
又∵EG⊥AC,
∴AG=CG=AC.
又∵AC=8,
∴AG=CG=4.
在直角△ABE中,AE=5,AG=4,则由勾股定理知:EG==3.
∴S==12.
24.如图,将一个长方形放置在平面直角坐标系中,OA=2,OC=3,E是AB中点,反比例函数图象过点E且和BC相交点F.
(1)直接写出点B和点E的坐标;
(2)求直线OB与反比例函数的解析式;
(3)连接OE、OF,求四边形OEBF的面积.
【分析】(1)根据OA=2,OC=3,得到点B的坐标;
(2)运用待定系数法求直线OB的解析式,根据E是AB的中点,求得点E的坐标,再进一步运用待定系数法求得反比例函数的解析式;
(3)根据反比例函数的解析式求得点F的横坐标,再进一步根据四边形的面积等于矩形的面积减去两个直角三角形的面积进行计算.
解:(1)∵OA=2,OC=3,E是AB中点,
∴B(2,3),E(2,);
(2)设直线OB的解析式是y=k1x,
把B点坐标代入,得k1=,
则直线OB的解析式是y=x.
设反比例函数解析式是y=,
把E点坐标代入,得k2=3,
则反比例函数的解析式是y=;
(2)由题意得Fy=3,代入,
得Fx=1,即F(1,3).
则四边形OEBF的面积=矩形OABC的面积﹣△OAE的面积﹣△OCF的面积=2×3﹣1×3﹣2×=3.
25.已知:在△ABC中,∠BAC=90°,AB=AC,点D为BC边上一动点(与点B不重合),连接AD,以AD始边作∠DAE=α(0°<α<180°).
(1)如图1,当α=90°,且AE=AD时,试说明CE和BD的位置关系和数量关系;
(2)如图2,当α=45°,且点E在边BC上时,求证:BD2+CE2=DE2.
【分析】(1)根据∠BAD=∠CAE,BA=CA,AD=AE,运用“SAS”证明△ABD≌△ACE,根据全等三角形性质得出对应边相等,对应角相等,即可得到线段CE、BD之间的关系;
(2)把△ACE绕点A顺时针旋转90°,得到△ABG.连接DG,由“SAS”得到△ADG≌△ADE,可得DE=DG,即可把EF,BE,FC放到一个直角三角形中,从而根据勾股定理即可证明;
解:(1)CE与BD位置关系是CE⊥BD,数量关系是CE=BD.
理由:∵∠BAC=∠DAE=90°,
∴∠BAD=90°﹣∠DAC,∠CAE=90°﹣∠DAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE (SAS),
∴∠ACE=∠B=45°且 CE=BD.
∵∠ACB=∠B=45°,
∴∠ECB=45°+45°=90°,即CE⊥BD;
(2)如图2,把△ACE绕点A顺时针旋转90°,得到△ABG.连接DG,
则△ACE≌△ABG,
∴AG=AE,BG=CE,∠ABG=∠ACE=45°.
∵∠BAC=90°,∠GAE=90°.
∴∠GAD=∠DAE=45°,
在△ADG和△ADE中,
,
∴△ADG≌△ADE(SAS).
∴ED=GD,
又∵∠GBD=90°,
∴BD2+BG2=DG2,
即BD2+EC2=DE2;
同课章节目录
