沪科版九年级下册数学单元测试卷 第24章 圆(word版无答案)
文档属性
| 名称 | 沪科版九年级下册数学单元测试卷 第24章 圆(word版无答案) | 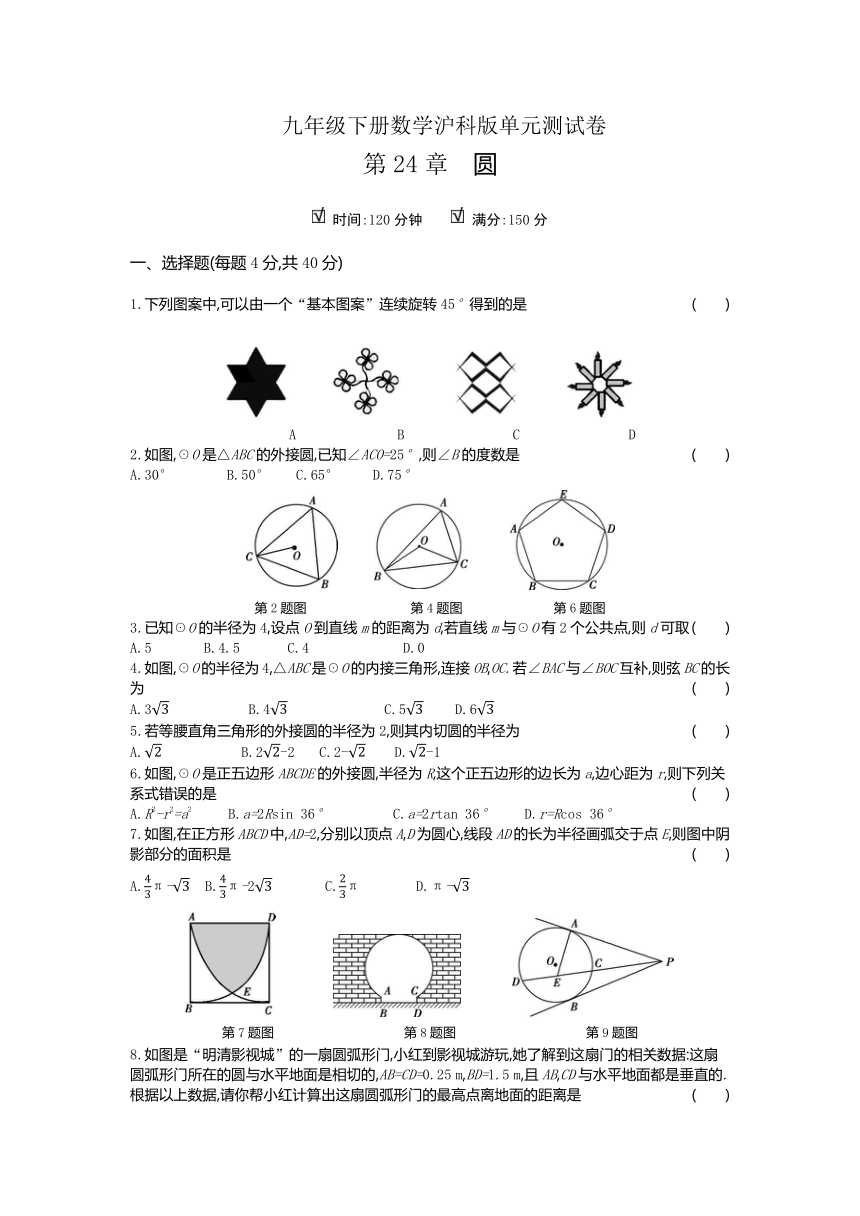 | |
| 格式 | zip | ||
| 文件大小 | 171.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-06 15:02:02 | ||
图片预览

文档简介
九年级下册数学沪科版单元测试卷
第24章 圆
时间:120分钟
满分:150分
一、选择题(每题4分,共40分)
1.下列图案中,可以由一个“基本图案”连续旋转45°得到的是
( )
A B
C
D
2.如图,☉O是△ABC的外接圆,已知∠ACO=25°,则∠B的度数是
( )
A.30°
B.50°
C.65°
D.75°
第2题图 第4题图 第6题图
3.已知☉O的半径为4,设点O到直线m的距离为d,若直线m与☉O有2个公共点,则d可取
( )
A.5
B.4.5
C.4
D.0
4.如图,☉O的半径为4,△ABC是☉O的内接三角形,连接OB,OC.若∠BAC与∠BOC互补,则弦BC的长为
( )
A.3
B.4
C.5
D.6
5.若等腰直角三角形的外接圆的半径为2,则其内切圆的半径为
( )
A.
B.2-2
C.2-
D.-1
6.如图,☉O是正五边形ABCDE的外接圆,半径为R,这个正五边形的边长为a,边心距为r,则下列关系式错误的是
( )
A.R2-r2=a2
B.a=2Rsin
36°
C.a=2rtan
36°
D.r=Rcos
36°
7.如图,在正方形ABCD中,AD=2,分别以顶点A,D为圆心,线段AD的长为半径画弧交于点E,则图中阴影部分的面积是
( )
A.π-
B.π-2
C.π
D.π-
第7题图
第8题图 第9题图
8.如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,她了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25
m,BD=1.5
m,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是
( )
A.2
m
B.2.5
m
C.2.4
m
D.2.1
m
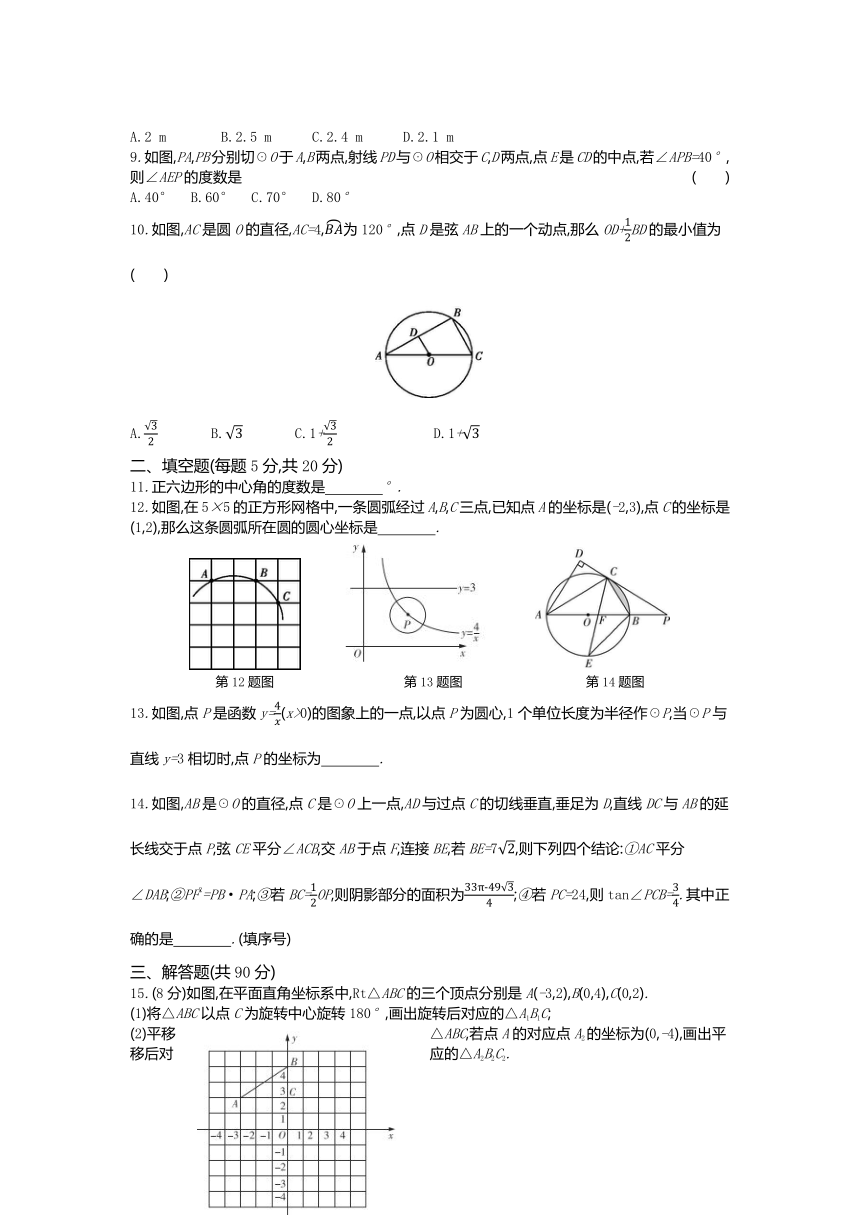
9.如图,PA,PB分别切☉O于A,B两点,射线PD与☉O相交于C,D两点,点E是CD的中点,若∠APB=40°,则∠AEP的度数是
( )
A.40°
B.60°
C.70°
D.80°
10.如图,AC是圆O的直径,AC=4,为120°,点D是弦AB上的一个动点,那么OD+BD的最小值为( )
A.
B.
C.1+
D.1+
二、填空题(每题5分,共20分)
11.正六边形的中心角的度数是 °.?
12.如图,在5×5的正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(-2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是 .?
第12题图 第13题图
第14题图
13.如图,点P是函数y=(x>0)的图象上的一点,以点P为圆心,1个单位长度为半径作☉P,当☉P与直线y=3相切时,点P的坐标为 .?
14.如图,AB是☉O的直径,点C是☉O上一点,AD与过点C的切线垂直,垂足为D,直线DC与AB的延长线交于点P,弦CE平分∠ACB,交AB于点F,连接BE,若BE=7,则下列四个结论:①AC平分∠DAB;②PF2=PB·PA;③若BC=OP,则阴影部分的面积为;④若PC=24,则tan∠PCB=.其中正确的是 .(填序号)?
三、解答题(共90分)
15.(8分)如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2.
16.(8分)如图,BD,CE是△ABC的高,M为BC的中点.试说明点B,C,D,E在以点M为圆心的同一个圆上.
17.(8分)如图,△ABC与△ADE都是直角三角形,连接CD,BE,CD与BE相交于点O,△BAE可看作是由△CAD顺时针旋转得到的.
(1)旋转中心是 ,旋转角度是 ;?
(2)判断CD与BE的位置关系,并说明理由.
18.(8分)如图,等腰三角形ABC内接于半径为5的☉O,AB=AC,tan∠ABC=.求BC的长.
19.(10分)如图,正方形ABCD内接于☉O,M为的中点,连接BM,CM.
(1)求证:BM=CM;
(2)当☉O的半径为2时,求的长.
20.(10分)如图,点A是以BC为直径的圆上的一点,BE是☉O的切线,CA的延长线与BE相交于点E,F是BE的中点,分别延长AF与CB交于点P.
(1)求证:PA是☉O的切线;
(2)若AF=3,BC=8,求AE的长.
21.(12分)如图,AB是半圆O的直径,点C是上一点,现将半圆O沿BC折叠,恰好过圆心O,点D为BC延长线上一点,且AD与半圆O相切.
(1)求∠ABC的度数;
(2)若半圆O的直径为6,求CD的长.
22.(12分)如图,☉O的直径AB为10
cm,弦BC为5
cm,D,E分别是∠ACB的平分线与☉O,AB的交点,P为AB延长线上一点,且PC=PE,连接AD.
(1)求AD的长;
(2)试判断直线PC与☉O的位置关系,并说明理由.
23.(14分)如图1,在Rt△OGF中,∠GOF=90°,OF=2,∠GFO=30°.
(1)OG= ;?
(2)若☉O的半径为1,交直线OF于点C,点P是直线GF上的动点,PA,PB分别切☉O于点A,B.
①求PB的最小值;
②连接BC,AC,如图2所示,若∠BCA=54°,求∠APB的度数;
③在直线GF上是否存在点P,使得∠APB=60°?若存在,请求出FP的长;若不存在,请说明理由.
图1 图2
第24章 圆
时间:120分钟
满分:150分
一、选择题(每题4分,共40分)
1.下列图案中,可以由一个“基本图案”连续旋转45°得到的是
( )
A B
C
D
2.如图,☉O是△ABC的外接圆,已知∠ACO=25°,则∠B的度数是
( )
A.30°
B.50°
C.65°
D.75°
第2题图 第4题图 第6题图
3.已知☉O的半径为4,设点O到直线m的距离为d,若直线m与☉O有2个公共点,则d可取
( )
A.5
B.4.5
C.4
D.0
4.如图,☉O的半径为4,△ABC是☉O的内接三角形,连接OB,OC.若∠BAC与∠BOC互补,则弦BC的长为
( )
A.3
B.4
C.5
D.6
5.若等腰直角三角形的外接圆的半径为2,则其内切圆的半径为
( )
A.
B.2-2
C.2-
D.-1
6.如图,☉O是正五边形ABCDE的外接圆,半径为R,这个正五边形的边长为a,边心距为r,则下列关系式错误的是
( )
A.R2-r2=a2
B.a=2Rsin
36°
C.a=2rtan
36°
D.r=Rcos
36°
7.如图,在正方形ABCD中,AD=2,分别以顶点A,D为圆心,线段AD的长为半径画弧交于点E,则图中阴影部分的面积是
( )
A.π-
B.π-2
C.π
D.π-
第7题图
第8题图 第9题图
8.如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,她了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25
m,BD=1.5
m,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是
( )
A.2
m
B.2.5
m
C.2.4
m
D.2.1
m
9.如图,PA,PB分别切☉O于A,B两点,射线PD与☉O相交于C,D两点,点E是CD的中点,若∠APB=40°,则∠AEP的度数是
( )
A.40°
B.60°
C.70°
D.80°
10.如图,AC是圆O的直径,AC=4,为120°,点D是弦AB上的一个动点,那么OD+BD的最小值为( )
A.
B.
C.1+
D.1+
二、填空题(每题5分,共20分)
11.正六边形的中心角的度数是 °.?
12.如图,在5×5的正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(-2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是 .?
第12题图 第13题图
第14题图
13.如图,点P是函数y=(x>0)的图象上的一点,以点P为圆心,1个单位长度为半径作☉P,当☉P与直线y=3相切时,点P的坐标为 .?
14.如图,AB是☉O的直径,点C是☉O上一点,AD与过点C的切线垂直,垂足为D,直线DC与AB的延长线交于点P,弦CE平分∠ACB,交AB于点F,连接BE,若BE=7,则下列四个结论:①AC平分∠DAB;②PF2=PB·PA;③若BC=OP,则阴影部分的面积为;④若PC=24,则tan∠PCB=.其中正确的是 .(填序号)?
三、解答题(共90分)
15.(8分)如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2.
16.(8分)如图,BD,CE是△ABC的高,M为BC的中点.试说明点B,C,D,E在以点M为圆心的同一个圆上.
17.(8分)如图,△ABC与△ADE都是直角三角形,连接CD,BE,CD与BE相交于点O,△BAE可看作是由△CAD顺时针旋转得到的.
(1)旋转中心是 ,旋转角度是 ;?
(2)判断CD与BE的位置关系,并说明理由.
18.(8分)如图,等腰三角形ABC内接于半径为5的☉O,AB=AC,tan∠ABC=.求BC的长.
19.(10分)如图,正方形ABCD内接于☉O,M为的中点,连接BM,CM.
(1)求证:BM=CM;
(2)当☉O的半径为2时,求的长.
20.(10分)如图,点A是以BC为直径的圆上的一点,BE是☉O的切线,CA的延长线与BE相交于点E,F是BE的中点,分别延长AF与CB交于点P.
(1)求证:PA是☉O的切线;
(2)若AF=3,BC=8,求AE的长.
21.(12分)如图,AB是半圆O的直径,点C是上一点,现将半圆O沿BC折叠,恰好过圆心O,点D为BC延长线上一点,且AD与半圆O相切.
(1)求∠ABC的度数;
(2)若半圆O的直径为6,求CD的长.
22.(12分)如图,☉O的直径AB为10
cm,弦BC为5
cm,D,E分别是∠ACB的平分线与☉O,AB的交点,P为AB延长线上一点,且PC=PE,连接AD.
(1)求AD的长;
(2)试判断直线PC与☉O的位置关系,并说明理由.
23.(14分)如图1,在Rt△OGF中,∠GOF=90°,OF=2,∠GFO=30°.
(1)OG= ;?
(2)若☉O的半径为1,交直线OF于点C,点P是直线GF上的动点,PA,PB分别切☉O于点A,B.
①求PB的最小值;
②连接BC,AC,如图2所示,若∠BCA=54°,求∠APB的度数;
③在直线GF上是否存在点P,使得∠APB=60°?若存在,请求出FP的长;若不存在,请说明理由.
图1 图2
