正、余弦函数的性质(1)
图片预览







文档简介
(共24张PPT)
1.4.2正弦函数余弦函数的性质
正弦函数y=sinx,x∈[0, 2 ]的图象中,
五个关键点是哪几个
余弦函数y=cosx,x∈[0, 2 ]的图象中,
五个关键点是哪几个
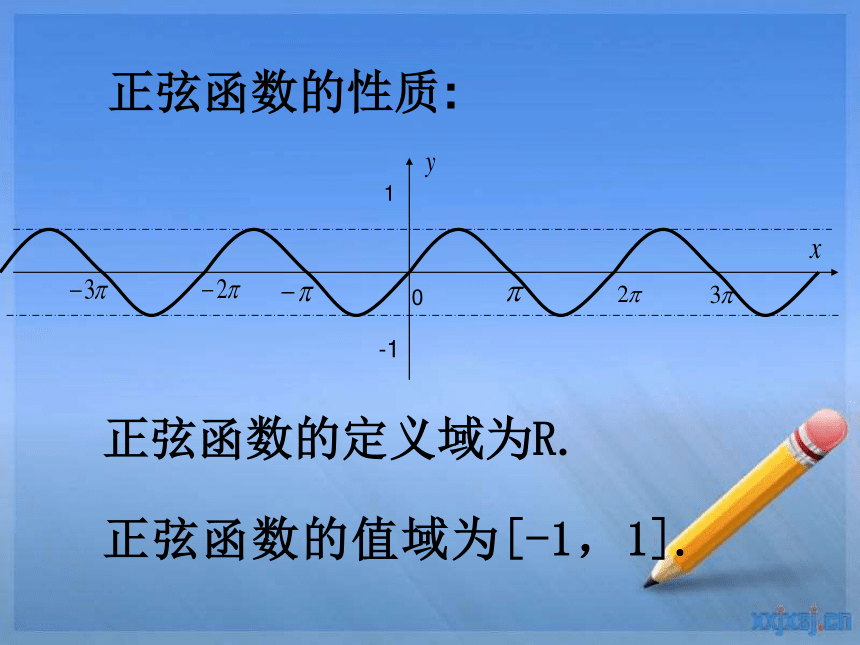
正弦函数的性质:
正弦函数的值域为[-1,1].
正弦函数的定义域为R.
-1
1
0
讲授新课
问题:
(1)今天是星期一,则过了七天是星期几?
过了十四天呢?……
(2)物理中的单摆振动、圆周运动,质点
运动的规律如何呢?
地球绕太阳公转
月相下半月变化
π
4
-
3 /2
o
-
π
2
-
π
3
-
/2
π
2
π
3
π
4
x
y
1
-1
观察正(余)弦函数的图象
我们发现正弦函数的图像是由这样一条曲线重复得到的。
讲授新课
所以
(1)正弦函数的图像是有规律不断重复出现的。
是否像上述的事物一样也有
这样周而复始的变化
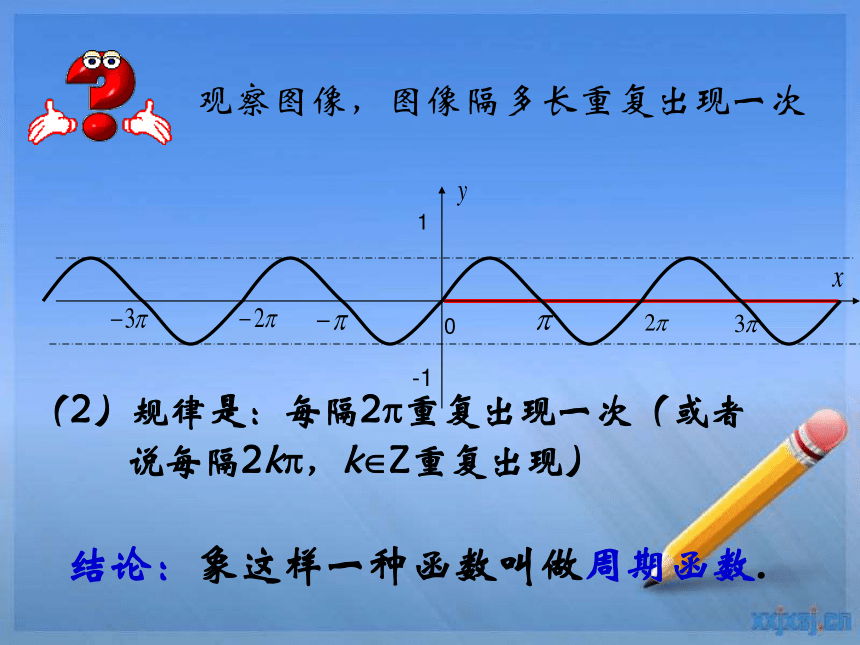
(2)规律是:每隔2 重复出现一次(或者
说每隔2k ,k Z重复出现)
观察图像,图像隔多长重复出现一次
结论:象这样一种函数叫做周期函数.
-1
1
0
讲授新课
1、周期函数定义:
对于函数f(x),如果存在一个非零
常数T,使得当x取定义域内的每一个
值时,都有:f (x+T)=f(x).那么函数
f(x)就叫做周期函数,非零常数T 叫做
这个函数的周期.
由诱导公式一:
所以由定义知正弦函数的周期
注:如果在周期函数f(x)的所有周期中存在一个最
小的正数T, 则这个最小正数叫做f(x)的最小正周期.
1、正弦函数的最小正周期是多少?
2、是否所有的周期函数都具有最小正周期?
3、如果不加特殊说明,教科书说到的
周期,一般都是指函数的最小正周
期?
讲授新课
答:存在,
因为最小的正数是1,当K=1是,T=2
答:否,如函数f(x)=3没有最小正周期
问题:
对于函数
有
能否说它的周期是
答:不能,因为定义要求对定义域内每一个都成立,而
对于函数f(x),如果存在一个非零
常数T,使得当x取定义域内的每一个
值时,都有:f (x+T)=f(x).那么函数
f(x)就叫做周期函数,非零常数T叫做
这个函数的周期.
根据上述定义,我们有:
正弦函数是周期函数,2K (K∈Z),都是它的
周期,最小正周期是2
类似的请同学们自己探索一下余弦函数的周期性,并写出余弦函数的周期。
π
4
-
3 /2
o
-
π
2
-
π
3
-
/2
π
2
π
3
π
4
y
1
-1
x
由余弦函数的图像可知,余弦函数也是周期函数,
最小正周期是2 ,由诱导公式
周期T=2K (K∈Z)
例题讲解
求下列函数的周期
(1)因为
所以有周期函数的定义可知,
原函数的周期为T=2
所以由周期的定义可知,
原函数的周期为T=
例题讲解
例题讲解
所以由周期的定义可知,
原函数的周期为T=4
例题讲解
所以由周期的定义可知,原函数的周期为T=
所以由周期的定义可知,原函数的周期为T=4
正弦函数,余弦函数
最小正周期是T=2
思考:
从前面的例子中可以看出,函数
及函数
练一练
1、求下列函数的周期:
练一练
2、函数 的周期是多少?
先观察一下函数图像:
由图像可知
练一练
正弦函数的性质:
-1
x
O
1
π
2π
3π
4π
5π
6π
-2π
-3π
-4π
-5π
-6π
-π
观察正弦函数图像,X取何值时,Y取最大值?
根据正弦函数的周期性可知
根据最大值,能不能写出X为何值时,
y最小值?
-1
1
0
1、周期函数的定义。
2、函数
的周期。
思考
-1
1
0
2
3
p
由图象可知:正弦函数的图象是否中心对称?
除了原点以外是否还存在其他的对称中心
1.4.2正弦函数余弦函数的性质
正弦函数y=sinx,x∈[0, 2 ]的图象中,
五个关键点是哪几个
余弦函数y=cosx,x∈[0, 2 ]的图象中,
五个关键点是哪几个
正弦函数的性质:
正弦函数的值域为[-1,1].
正弦函数的定义域为R.
-1
1
0
讲授新课
问题:
(1)今天是星期一,则过了七天是星期几?
过了十四天呢?……
(2)物理中的单摆振动、圆周运动,质点
运动的规律如何呢?
地球绕太阳公转
月相下半月变化
π
4
-
3 /2
o
-
π
2
-
π
3
-
/2
π
2
π
3
π
4
x
y
1
-1
观察正(余)弦函数的图象
我们发现正弦函数的图像是由这样一条曲线重复得到的。
讲授新课
所以
(1)正弦函数的图像是有规律不断重复出现的。
是否像上述的事物一样也有
这样周而复始的变化
(2)规律是:每隔2 重复出现一次(或者
说每隔2k ,k Z重复出现)
观察图像,图像隔多长重复出现一次
结论:象这样一种函数叫做周期函数.
-1
1
0
讲授新课
1、周期函数定义:
对于函数f(x),如果存在一个非零
常数T,使得当x取定义域内的每一个
值时,都有:f (x+T)=f(x).那么函数
f(x)就叫做周期函数,非零常数T 叫做
这个函数的周期.
由诱导公式一:
所以由定义知正弦函数的周期
注:如果在周期函数f(x)的所有周期中存在一个最
小的正数T, 则这个最小正数叫做f(x)的最小正周期.
1、正弦函数的最小正周期是多少?
2、是否所有的周期函数都具有最小正周期?
3、如果不加特殊说明,教科书说到的
周期,一般都是指函数的最小正周
期?
讲授新课
答:存在,
因为最小的正数是1,当K=1是,T=2
答:否,如函数f(x)=3没有最小正周期
问题:
对于函数
有
能否说它的周期是
答:不能,因为定义要求对定义域内每一个都成立,而
对于函数f(x),如果存在一个非零
常数T,使得当x取定义域内的每一个
值时,都有:f (x+T)=f(x).那么函数
f(x)就叫做周期函数,非零常数T叫做
这个函数的周期.
根据上述定义,我们有:
正弦函数是周期函数,2K (K∈Z),都是它的
周期,最小正周期是2
类似的请同学们自己探索一下余弦函数的周期性,并写出余弦函数的周期。
π
4
-
3 /2
o
-
π
2
-
π
3
-
/2
π
2
π
3
π
4
y
1
-1
x
由余弦函数的图像可知,余弦函数也是周期函数,
最小正周期是2 ,由诱导公式
周期T=2K (K∈Z)
例题讲解
求下列函数的周期
(1)因为
所以有周期函数的定义可知,
原函数的周期为T=2
所以由周期的定义可知,
原函数的周期为T=
例题讲解
例题讲解
所以由周期的定义可知,
原函数的周期为T=4
例题讲解
所以由周期的定义可知,原函数的周期为T=
所以由周期的定义可知,原函数的周期为T=4
正弦函数,余弦函数
最小正周期是T=2
思考:
从前面的例子中可以看出,函数
及函数
练一练
1、求下列函数的周期:
练一练
2、函数 的周期是多少?
先观察一下函数图像:
由图像可知
练一练
正弦函数的性质:
-1
x
O
1
π
2π
3π
4π
5π
6π
-2π
-3π
-4π
-5π
-6π
-π
观察正弦函数图像,X取何值时,Y取最大值?
根据正弦函数的周期性可知
根据最大值,能不能写出X为何值时,
y最小值?
-1
1
0
1、周期函数的定义。
2、函数
的周期。
思考
-1
1
0
2
3
p
由图象可知:正弦函数的图象是否中心对称?
除了原点以外是否还存在其他的对称中心
