3.6梯形的中位线

教学内 容 3.6 梯形的中位线 共 几 课 时 1 课 型 新课
第 几 课 时 1
教学 目 标 1．掌握梯形中位线的概念和梯形中位线定理。2．能够应用梯形中位线概念及定理进行有关的论证和计算，进一步提高学生的计算能力和分析能力。
重 点难 点 重点：梯形中位线定理的证明。难点：性质应用中辅助线的添设．
教 学 资 源 多媒体
预 习 设 计
学 生 活 动 设 计 教 师 导 学 设 计 教学反思修改意见
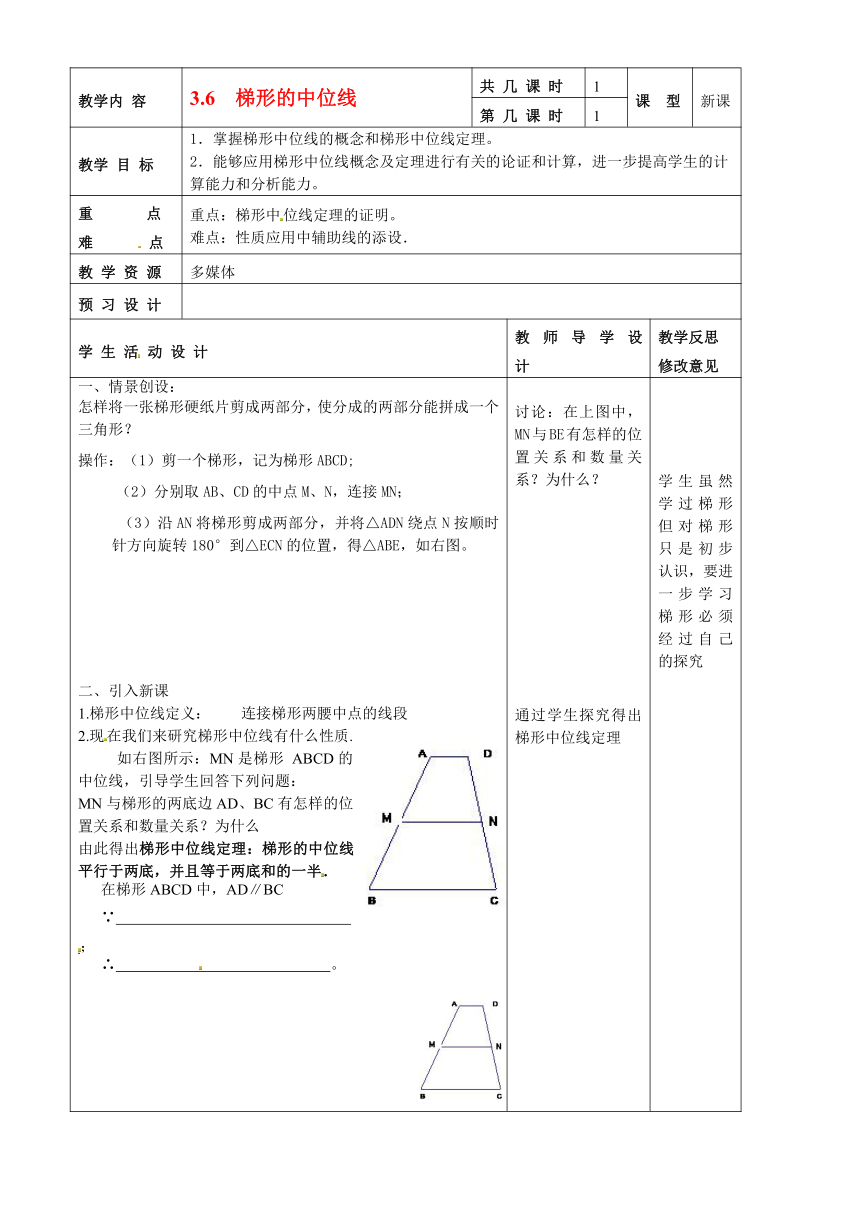
一、情景创设：怎样将一张梯形硬纸片剪成两部分，使分成的两部分能拼成一个三角形？操作：（1）剪一个梯形，记为梯形ABCD; （2）分别取AB、CD的中点M、N，连接MN；（3）沿AN将梯形剪成两部分，并将△ADN绕点N按顺时针方向旋转180°到△ECN的位置，得△ABE，如右图。二、引入新课1.梯形中位线定义： 连接梯形两腰中点的线段 2.现在我们来研究梯形中位线有什么性质.　 如右图所示：MN是梯形 ABCD的中位线，引导学生回答下列问题：MN与梯形的两底边AD、BC有怎样的位置关系和数量关系？为什么由此得出梯形中位线定理：梯形的中位线平行于两底，并且等于两底和的一半.在梯形ABCD中，AD∥BC∵ ；∴ 。 讨论：在上图中，MN与BE有怎样的位置关系和数量关系？为什么？通过学生探究得出梯形中位线定理 学生虽然学过梯形但对梯形只是初步认识，要进一步学习梯形必须经过自己的探究
3． 归纳总结出梯形的又一个面积公式：S 梯=(a+b)h 设中位线长为l ,则l =(a+b), S=l*h三、典例分析例1.如图，梯子各横木条互相平行，且A1A2=A2A3=A3A4=A4A5,B1B2=B2B3=B3B4=B4B5。已知横木条A1B1=48cm，A2B2=44cm,求横木条A3B3、A4B4、A5B5的长。例2：已知：如图在梯形ABCD中，AD∥BC， AB＝AD＋BC，P为CD的中点，求证：AP⊥BP 四、拓展练习 1、已知，等腰梯形ABCD中，两条对角线AC、BD互相垂直，中位线EF长为8cm，求它的高CH。2、已知，在梯形ABCD中，AD∥BC，对角线AC⊥BD，且AC＝12，BD＝9，则此梯形的中位线长是 …（ ）A．10　　B．　　C．　　 D．12 五、小结：1、基本知识：梯形中位线定理（位置关系：梯形的中位线平行于上、下底；数量关系：梯形的中位线等于上下底和的一半。把梯形的中位线定理与三角形中位线定理进行比较，三角形实质上可以理解为上底为零的一种特殊的梯形）2、梯形另一面积计算公式3、数学思想方法：化归、几何建模、数形结合 例1用梯形中位线性质解题，过程书写要注意例2是一个典型的题目，注意辅助性的作法，引导学生如何写解题过程 梯形辅助性的作法是梯形部分的重要内容，可以利用单独一节课对梯形辅助线作法加以练习，归纳、总结
作业设计 课中检测 一、填空①一个梯形的上底长4 cm，下底长6 cm，则其中位线长为 cm；②一个梯形的上底长10 cm，中位线长16 cm，则其下底长为 cm；③已知梯形的中位线长为6 cm，高为8 cm，则该梯形的面积为________ cm2 ；④已知等腰梯形的周长为80 cm，中位线与腰长相等，则它的中位线长 cm；5．若梯形的上底长为8cm,,中位线长10cm,则下底长为 。6．等腰梯形ABCD的中位线EF的长为6，腰AD的长为5，则等腰梯形ABCD的周长为 。7．若梯形的周长为80cm, 中位线长于腰长相等，高为12cm,则它的面积为 。5．一个等腰梯形的对角线互相垂直，梯形的高为2cm,，则梯形的面积为 。