2020-2021学年北师大新版七年级下册《第3章 变量之间的关系》2020年单元测试卷(有答案)
文档属性
| 名称 | 2020-2021学年北师大新版七年级下册《第3章 变量之间的关系》2020年单元测试卷(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 291.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-06 22:41:15 | ||
图片预览


文档简介
2020-2021学年北师大新版七年级下册《第3章
变量之间的关系》单元测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下面的关系:
x
0
1
2
3
4
5
y
10
10.5
11
11.5
12
12.5
下列说法不正确的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.物体质量每增加1kg,弹簧长度y增加0.5cm
C.y与x的关系表达式是y=0.5x
D.所挂物体质量为7kg时,弹簧长度为13.5cm
2.如图,在长方形网格中,每个小长方形的长为2,宽为1,A、B两点在网格格点上,若点C也在网格格点上,以A、B、C为顶点的三角形面积为2,则满足条件的点C个数是( )
A.2
B.3
C.4
D.5
3.如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落到点C′处;作∠BPC′的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A.
B.
C.
D.
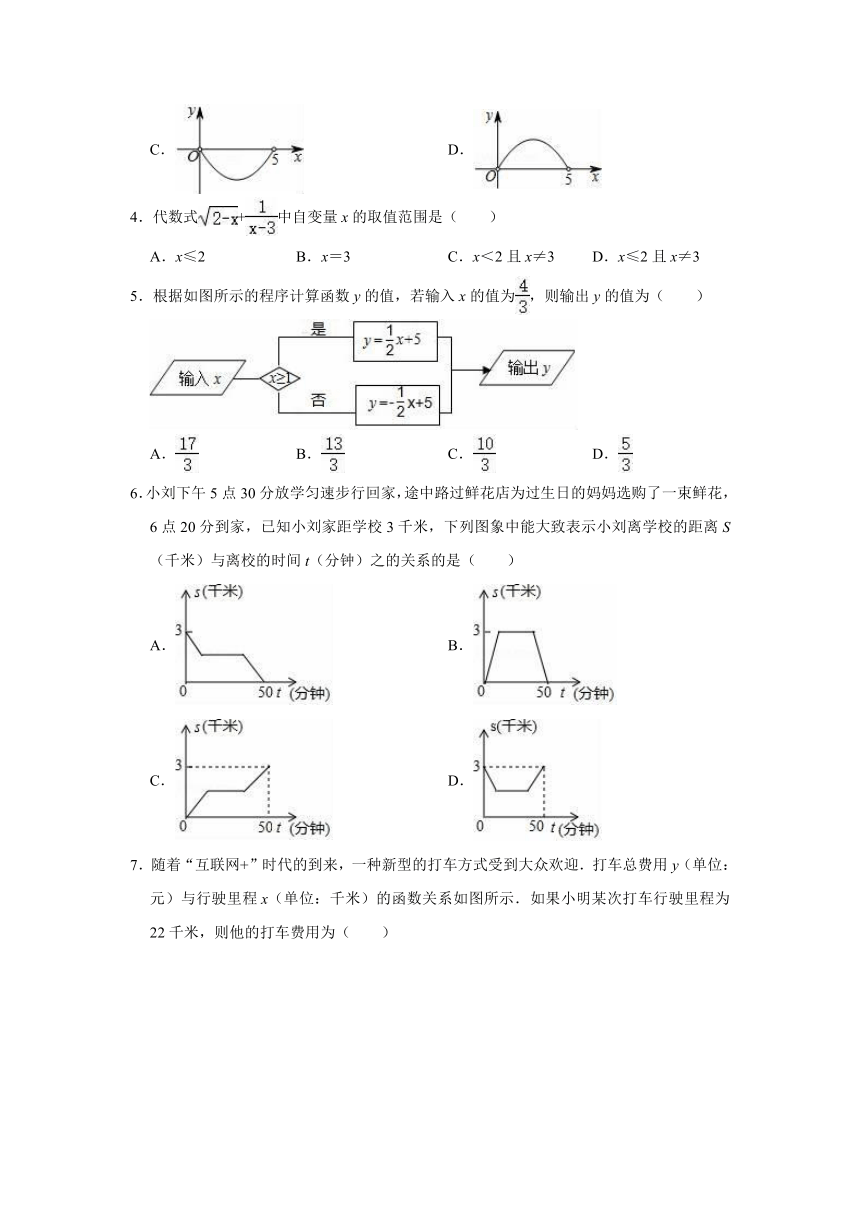
4.代数式+中自变量x的取值范围是( )
A.x≤2
B.x=3
C.x<2且x≠3
D.x≤2且x≠3
5.根据如图所示的程序计算函数y的值,若输入x的值为,则输出y的值为( )
A.
B.
C.
D.
6.小刘下午5点30分放学匀速步行回家,途中路过鲜花店为过生日的妈妈选购了一束鲜花,6点20分到家,已知小刘家距学校3千米,下列图象中能大致表示小刘离学校的距离S(千米)与离校的时间t(分钟)之的关系的是( )
A.
B.
C.
D.
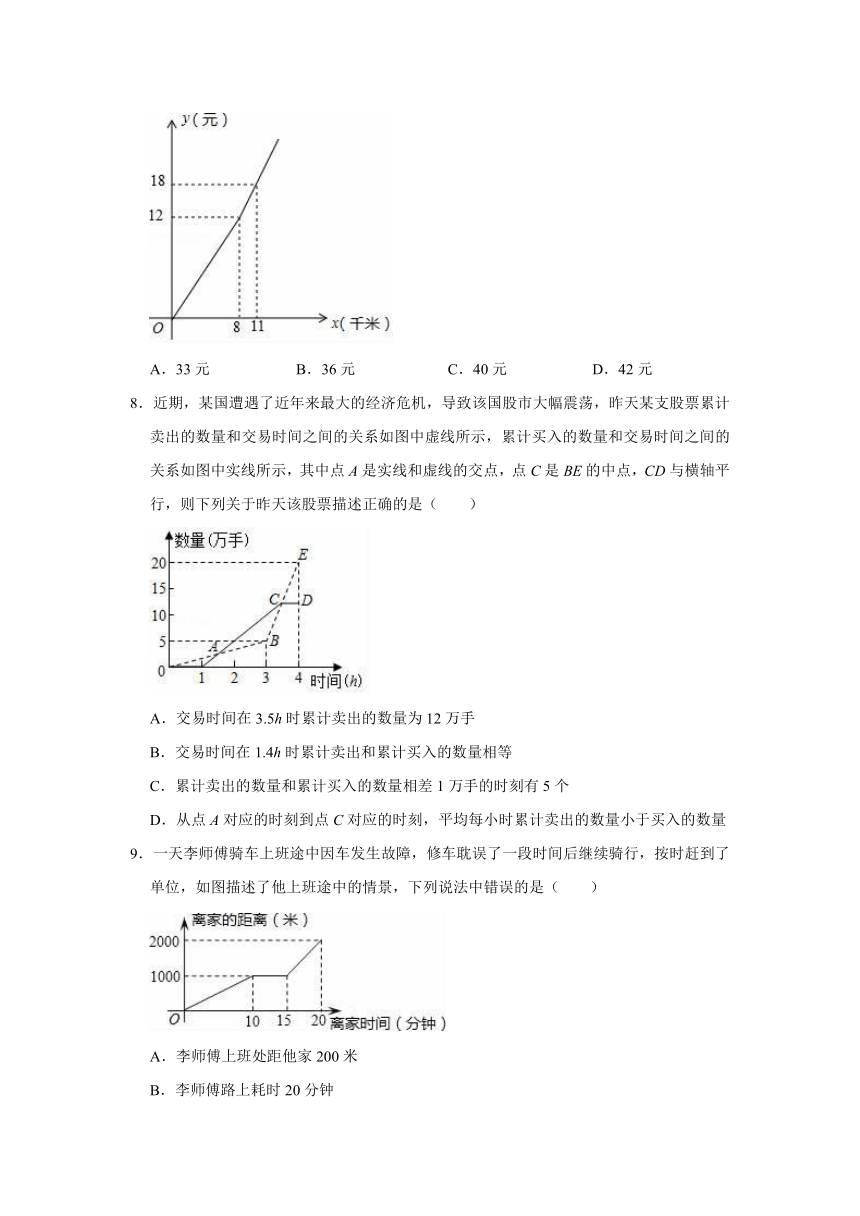
7.随着“互联网+”时代的到来,一种新型的打车方式受到大众欢迎.打车总费用y(单位:元)与行驶里程x(单位:千米)的函数关系如图所示.如果小明某次打车行驶里程为22千米,则他的打车费用为( )
A.33元
B.36元
C.40元
D.42元
8.近期,某国遭遇了近年来最大的经济危机,导致该国股市大幅震荡,昨天某支股票累计卖出的数量和交易时间之间的关系如图中虚线所示,累计买入的数量和交易时间之间的关系如图中实线所示,其中点A是实线和虚线的交点,点C是BE的中点,CD与横轴平行,则下列关于昨天该股票描述正确的是( )
A.交易时间在3.5h时累计卖出的数量为12万手
B.交易时间在1.4h时累计卖出和累计买入的数量相等
C.累计卖出的数量和累计买入的数量相差1万手的时刻有5个
D.从点A对应的时刻到点C对应的时刻,平均每小时累计卖出的数量小于买入的数量
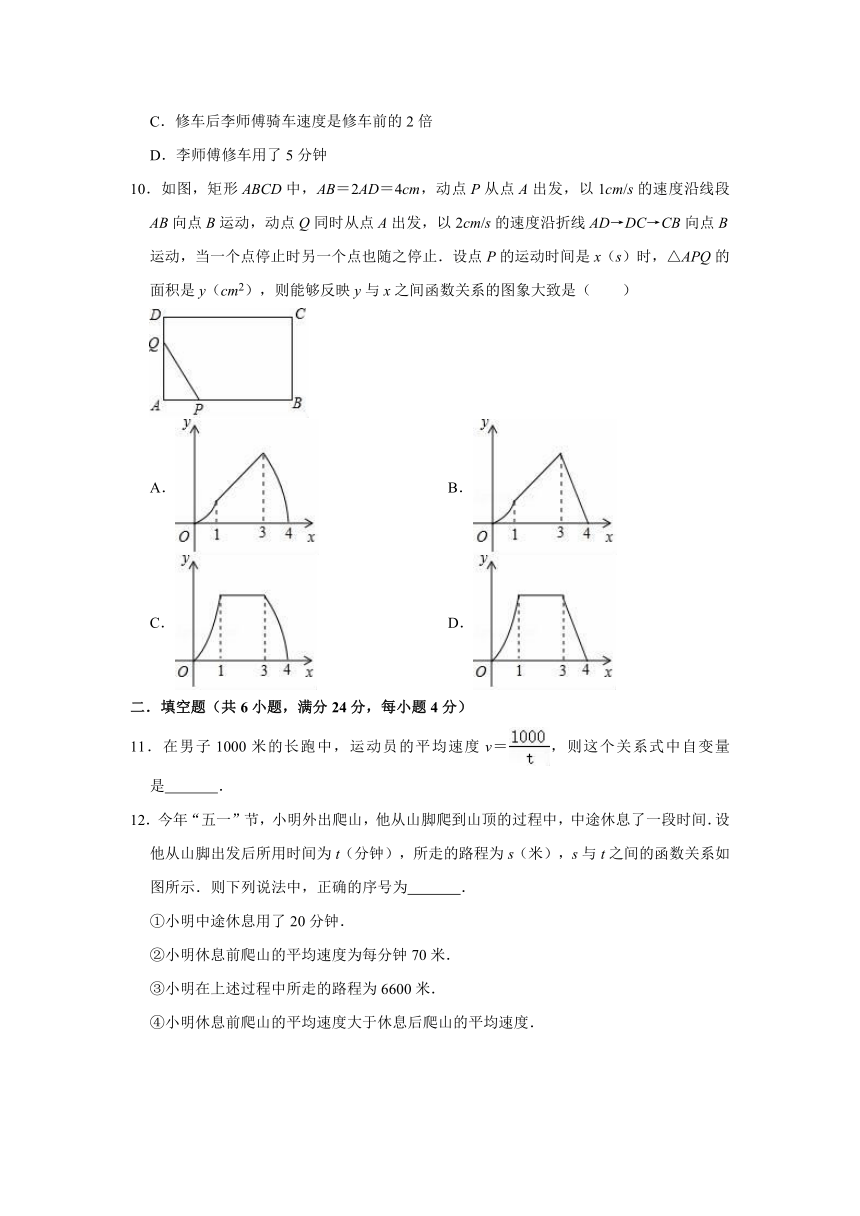
9.一天李师傅骑车上班途中因车发生故障,修车耽误了一段时间后继续骑行,按时赶到了单位,如图描述了他上班途中的情景,下列说法中错误的是( )
A.李师傅上班处距他家200米
B.李师傅路上耗时20分钟
C.修车后李师傅骑车速度是修车前的2倍
D.李师傅修车用了5分钟
10.如图,矩形ABCD中,AB=2AD=4cm,动点P从点A出发,以1cm/s的速度沿线段AB向点B运动,动点Q同时从点A出发,以2cm/s的速度沿折线AD→DC→CB向点B运动,当一个点停止时另一个点也随之停止.设点P的运动时间是x(s)时,△APQ的面积是y(cm2),则能够反映y与x之间函数关系的图象大致是( )
A.
B.
C.
D.
二.填空题(共6小题,满分24分,每小题4分)
11.在男子1000米的长跑中,运动员的平均速度v=,则这个关系式中自变量是
.
12.今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.则下列说法中,正确的序号为
.
①小明中途休息用了20分钟.
②小明休息前爬山的平均速度为每分钟70米.
③小明在上述过程中所走的路程为6600米.
④小明休息前爬山的平均速度大于休息后爬山的平均速度.
13.函数中,自变量x的取值范围是
.
14.某商场在“五一”期间举行促销活动,根据顾客按商品标价一次性购物总额,规定相应的优惠方法:①如果不超过500元,则不予优惠;
②如果超过500元,但不超过800元,则按购物总额给予8折优惠;
③如果超过800元,则其中800元给予8折优惠,超过800元的部分给予6折优惠.
促销期间,小红和她母亲分别看中一件商品,若各自单独付款,则应分别付款460元和560元;若合并付款,则她们总共只需付款
元.
15.某城市出租车收费按路程计算,3千米之内(包括3千米)收费6元,超过3千米每增加1千米加收1.6元,则车费y(元)与路程x(千米)之间的函数关系式为
.
16.如图,已知长方形ABCD中,点G在CD上,动点P从点B出发,以1个单位长度/s的速度沿折线B→C→G→F向终点F运动,设运动时间为x秒,△PAB的面积为y,y与x之间的函数关系图象如图所示.有以下结论:①AB=4;②y=2x(0≤x≤6);③AF=3;④DE=2;⑤S△ACF=6.则以上结论正确的有
(填序号).
三.解答题(共5小题,满分46分)
17.一辆汽车在公路上行驶,其所走的路程和所用的时间可用下表表示:
时间/t(min)
1
2.5
5
10
20
50
…
路程/s(km)
2
5
10
20
40
100
…
(1)在这个变化过程中,自变量、因变量各是什么?
(2)当汽车行驶路程s为20km时,所花的时间t是多少分钟?
(3)从表中说出随着t逐渐变大,s的变化趋势是什么?
(4)如果汽车行驶的时间为t(min),行驶的路程为s(km),那么路程s与时间t之间的关系式为
.
(5)按照这一行驶规律,当所花的时间t是300min时,汽车行驶的路程s是多少千米?
18.为了解某种品牌小汽车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表:
汽车行驶时间t(h)
0
1
2
3
…
油箱剩余油量Q(L)
100
94
88
82
…
(1)根据上表的数据,请你写出Q与t的关系式;
(2)汽车行驶5h后,油箱中的剩余油量是多少?
(3)该品牌汽车的油箱加50L,若以100km/h的速度匀速行驶,该车最多能行驶多远?
19.一个长方形的宽为xcm,长为ycm,面积为24cm2.
(1)求y与x之间的函数关系式;
(2)当x=8时,长方形的长为多少cm.
20.为了加强公民的节水意识,某地规定用水收费标准如下:每户每月用水量不超过6m3时,水费按每立方米1.1元收费,超过6m3时,超过部分每立方米按1.6元收费,设每户每月用水量为xm3,应缴水费为y元.
(1)写出y与x之间的函数表达式;
(2)如果有两户家庭某月份需缴纳水费为5.5元和9.8元时,求这两户家庭这个月的用水量分别是多少?
21.A、B两地相距90km,甲、乙两人从两地出发相向而行,甲先出发.图中l1,l2表示两人离A地的距离S(km)与时间t(h)的关系,结合图象回答下列问题:
(1)表示甲离A地的距离与时间关系的图象是
(填l1或l2);
甲的速度是
km/h;乙的速度是
km/h.
(2)甲出发后多少时间两人恰好相距15km?
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、y随x的增加而增加,x是自变量,y是因变量,故A选项正确;
B、物体质量每增加1kg,弹簧长度y增加0.5cm,故B选项正确;
C、y与x的关系表达式是y=0.5x+10,故C选项错误;
D、由C知,则当x=7时,y=13.5,即所挂物体质量为7kg时,弹簧长度为13.5cm,故D选项正确;
故选:C.
2.解:C点所有的情况如图所示:
故选:C.
3.解:如图,连接DE,∵△PC′D是△PCD沿PD折叠得到,
∴∠CPD=∠C′PD,
∵PE平分∠BPC′,
∴∠BPE=∠C′PE,
∴∠EPC′+∠DPC′=×180°=90°,
∴△DPE是直角三角形,
∵BP=x,BE=y,AB=3,BC=5,
∴AE=AB﹣BE=3﹣y,CP=BC﹣BP=5﹣x,
在Rt△BEP中,PE2=BP2+BE2=x2+y2,
在Rt△ADE中,DE2=AE2+AD2=(3﹣y)2+52,
在Rt△PCD中,PD2=PC2+CD2=(5﹣x)2+32,
在Rt△PDE中,DE2=PE2+PD2,
则(3﹣y)2+52=x2+y2+(5﹣x)2+32,
整理得,﹣6y=2x2﹣10x,
所以y=﹣x2+x(0<x<5),
纵观各选项,只有D选项符合.
故选:D.
4.解:由题意得,2﹣x≥0且x﹣3≠0,
解答x≤2且x≠3,
所以,自变量x的取值范围是x≤2.
故选:A.
5.解:∵x=≥1
∴x=应代入y=x+5,得y=
故选:A.
6.解:∵小刘家距学校3千米,
∴离校的距离随着时间的增大而增大,
∵路过鲜花店为过生日的妈妈选购了一束鲜花,
∴中间有一段离家的距离不再增大,离校50分钟后离校的距离最大,即3千米.
综合以上C符合,
故选:C.
7.解:当行驶里程x≥8时,设y=kx+b,
将(8,12)、(11,18)代入,
得:,
解得:,
∴y=2x﹣4,
当x=22时,y=2×22﹣4=40,
∴如果小明某次打车行驶里程为22千米,则他的打车费用为40元;
故选:C.
8.解:∵点B(3,5),点E(4,20),点C是BE的中点,
∴点C(,),
∴交易时间在3.5h时累计卖出的数量为12.5万手,故A选项不合题意;
∵直线OB过点(0,0),点B(3,5),
∴直线OB解析式为:y=x,
∵直线AC过点(1,0),点C(,),
∴直线AC解析式为:y=5x﹣5,
联立方程组可得,
∴
∴交易时间在1.5h时累计卖出和累计买入的数量相等,故B选项不合题意;
由图象可得累计卖出的数量和累计买入的数量相差1万手的时刻有4个,故C选项不合题意,
由图象可得从点A对应的时刻到点C对应的时刻,实线在虚线的上方,即平均每小时累计卖出的数量小于买入的数量,故D选项符合题意,
故选:D.
9.解:A、李师傅上班处距他家2000米,此选项错误;
B、李师傅路上耗时20分钟,此选项正确;
C、修车后李师傅骑车速度是=200米/分钟,修车前速度为=100米/分钟,
∴修车后李师傅骑车速度是修车前的2倍,此选项正确;
D、李师傅修车用了5分钟,此选项正确;
故选:A.
10.解:当点Q在AD上运动时,0≤x≤1,
y=?AP?AQ=?x?2x=x2;
当点Q在CD上运动时,1<x≤3,
y=?AP?AD=?x?2=x;
当点Q在CB上运动时,3<x≤4,
y=?AP?CB=?x?(8﹣2x)=﹣x2+4x,
故选:A.
二.填空题(共6小题,满分24分,每小题4分)
11.解:在男子1000米的长跑中,运动员的平均速度v=,则这个关系式中自变量是t,
故答案为:t.
12.解:①、根据图象可知,在40~60分钟,路程没有发生变化,所以小明中途休息的时间为:60﹣40=20分钟,故正确;
②、根据图象可知,当t=40时,s=2800,所以小明休息前爬山的平均速度为:2800÷40=70(米/分钟),故B正确;
③、根据图象可知,小明在上述过程中所走的路程为3800米,故错误;
④、小明休息后的爬山的平均速度为:(3800﹣2800)÷(100﹣60)=25(米/分),小明休息前爬山的平均速度为:2800÷40=70(米/分钟),
70>25,所以小明休息前爬山的平均速度大于休息后爬山的平均速度,故正确;
综上所述,正确的有①②④.
故答案为:①②④
13.解:根据题意得:x+5≠0,
解得:x≠﹣5.
故答案为:x≠﹣5.
14.解:由题意知付款460元,实际标价为460或460×=575(元),
付款560元,实际标价为560×=700(元),
如果一次购买标价460+700=1160(元)的商品应付款
800×0.8+(1160﹣800)×0.6=856(元).
如果一次购买标价575+700=1275(元)的商品应付款
800×0.8+(1275﹣800)×0.6=925(元).
故答案是:856或925.
15.解:根据题意得:
①当0<x≤3时,y=6;
②当x>3时,y=6+1.6(x﹣3)=1.6x+1.2;
∴车费y(元)与路程x(千米)之间的函数关系式为:y=.
故答案为:y=.
16.解:∵运动时间为x秒,△PAB的面积为y
∴观察图象可得,当点P到达点C时,y=4,x=2
∴×AB×2=4
∴AB=4
故①正确;
由函数图象可知,当0≤x≤2时,y=2x,当2<x≤4时,y=4
故②错误;
如图,连接AC,CF,AF
由图可知,AD=BC=2,CG=2,DE=GF=2
∴AE=2+2=4,EF=4﹣2=2
在Rt△AEF中,由勾股定理得:
AF==2
∴③错误;④正确;
∵S△ACF=S△ADC+S正方形DEFG+S△GCF﹣S△AEF
=×4×2+2×2+×2×2﹣×4×2
=4+4+2﹣4
=6
∴⑤正确;
故答案为:①④⑤.
三.解答题(共5小题,满分46分)
17.解:(1)自变量是时间,因变量是路程;
(2)∵当t=1时,s=2,
∴v===2,
∴t==10分钟;
(3)由表得,随着t逐渐变大,s逐渐变大(或者时间每增加1分钟,路程增加2千米);
(4)由(2)得v=2,
∴路程s与时间t之间的关系式为s=2t,
故答案为s=2t;
(5)把t=300代入s=2t,
得s=600.
18.解:(1)Q=100﹣6t;
(2)当t=5时,Q=100﹣6×5=70.
答:汽车行驶5h后,油箱中的剩余油量是70L;
(3)当Q=50时,50=100﹣6t,
6t=50,
解得:t=,
100×=km.
答:该车最多能行驶km.
19.解:(1)由题意可知:y=(x>0)
(2)当x=8时,
y==3
20.解:(1)由题意可得,
当0≤x≤6时,y=1.1x,
当x>6时,y=1.1×6+(x﹣6)×1.6=1.6x﹣3,
即y与x之间的函数表达式是y=;
(2)∵5.5<1.1×6,
∴缴纳水费为5.5元的用户用水量不超过6m3,
将y=5.5代入y=1.1x,解得x=5;
∵9.8>1.1×6,
∴缴纳水费为9.8元的用户用水量超过6m3,
将y=9.8代入y=1.6x﹣3,解得x=8;
答:这两户家庭这个月的用水量分别是5m3,8m3.
21.解:(1)∵甲先出发,
∴表示甲离A地的距离与时间关系的图象是l1,
甲的速度是:90÷2=45km/h,乙的速度是:90÷(3.5﹣0.5)=90÷3=30km/h,
故答案为:l1,45,30;
(2)设甲对应的函数解析式为y=ax+b,
,得,
∴甲对应的函数解析式为y=﹣45x+90,
设乙对应的函数解析式为y=cx+d,
,得,
即乙对应的函数解析式为y=30x﹣15,
∴|(﹣45x+90)﹣(30x﹣15)|=15,
解得,x1=1.2,x2=1.6,
答:甲出发后1.2h或1.6h时两人恰好相距15km.
变量之间的关系》单元测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下面的关系:
x
0
1
2
3
4
5
y
10
10.5
11
11.5
12
12.5
下列说法不正确的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.物体质量每增加1kg,弹簧长度y增加0.5cm
C.y与x的关系表达式是y=0.5x
D.所挂物体质量为7kg时,弹簧长度为13.5cm
2.如图,在长方形网格中,每个小长方形的长为2,宽为1,A、B两点在网格格点上,若点C也在网格格点上,以A、B、C为顶点的三角形面积为2,则满足条件的点C个数是( )
A.2
B.3
C.4
D.5
3.如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落到点C′处;作∠BPC′的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A.
B.
C.
D.
4.代数式+中自变量x的取值范围是( )
A.x≤2
B.x=3
C.x<2且x≠3
D.x≤2且x≠3
5.根据如图所示的程序计算函数y的值,若输入x的值为,则输出y的值为( )
A.
B.
C.
D.
6.小刘下午5点30分放学匀速步行回家,途中路过鲜花店为过生日的妈妈选购了一束鲜花,6点20分到家,已知小刘家距学校3千米,下列图象中能大致表示小刘离学校的距离S(千米)与离校的时间t(分钟)之的关系的是( )
A.
B.
C.
D.
7.随着“互联网+”时代的到来,一种新型的打车方式受到大众欢迎.打车总费用y(单位:元)与行驶里程x(单位:千米)的函数关系如图所示.如果小明某次打车行驶里程为22千米,则他的打车费用为( )
A.33元
B.36元
C.40元
D.42元
8.近期,某国遭遇了近年来最大的经济危机,导致该国股市大幅震荡,昨天某支股票累计卖出的数量和交易时间之间的关系如图中虚线所示,累计买入的数量和交易时间之间的关系如图中实线所示,其中点A是实线和虚线的交点,点C是BE的中点,CD与横轴平行,则下列关于昨天该股票描述正确的是( )
A.交易时间在3.5h时累计卖出的数量为12万手
B.交易时间在1.4h时累计卖出和累计买入的数量相等
C.累计卖出的数量和累计买入的数量相差1万手的时刻有5个
D.从点A对应的时刻到点C对应的时刻,平均每小时累计卖出的数量小于买入的数量
9.一天李师傅骑车上班途中因车发生故障,修车耽误了一段时间后继续骑行,按时赶到了单位,如图描述了他上班途中的情景,下列说法中错误的是( )
A.李师傅上班处距他家200米
B.李师傅路上耗时20分钟
C.修车后李师傅骑车速度是修车前的2倍
D.李师傅修车用了5分钟
10.如图,矩形ABCD中,AB=2AD=4cm,动点P从点A出发,以1cm/s的速度沿线段AB向点B运动,动点Q同时从点A出发,以2cm/s的速度沿折线AD→DC→CB向点B运动,当一个点停止时另一个点也随之停止.设点P的运动时间是x(s)时,△APQ的面积是y(cm2),则能够反映y与x之间函数关系的图象大致是( )
A.
B.
C.
D.
二.填空题(共6小题,满分24分,每小题4分)
11.在男子1000米的长跑中,运动员的平均速度v=,则这个关系式中自变量是
.
12.今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.则下列说法中,正确的序号为
.
①小明中途休息用了20分钟.
②小明休息前爬山的平均速度为每分钟70米.
③小明在上述过程中所走的路程为6600米.
④小明休息前爬山的平均速度大于休息后爬山的平均速度.
13.函数中,自变量x的取值范围是
.
14.某商场在“五一”期间举行促销活动,根据顾客按商品标价一次性购物总额,规定相应的优惠方法:①如果不超过500元,则不予优惠;
②如果超过500元,但不超过800元,则按购物总额给予8折优惠;
③如果超过800元,则其中800元给予8折优惠,超过800元的部分给予6折优惠.
促销期间,小红和她母亲分别看中一件商品,若各自单独付款,则应分别付款460元和560元;若合并付款,则她们总共只需付款
元.
15.某城市出租车收费按路程计算,3千米之内(包括3千米)收费6元,超过3千米每增加1千米加收1.6元,则车费y(元)与路程x(千米)之间的函数关系式为
.
16.如图,已知长方形ABCD中,点G在CD上,动点P从点B出发,以1个单位长度/s的速度沿折线B→C→G→F向终点F运动,设运动时间为x秒,△PAB的面积为y,y与x之间的函数关系图象如图所示.有以下结论:①AB=4;②y=2x(0≤x≤6);③AF=3;④DE=2;⑤S△ACF=6.则以上结论正确的有
(填序号).
三.解答题(共5小题,满分46分)
17.一辆汽车在公路上行驶,其所走的路程和所用的时间可用下表表示:
时间/t(min)
1
2.5
5
10
20
50
…
路程/s(km)
2
5
10
20
40
100
…
(1)在这个变化过程中,自变量、因变量各是什么?
(2)当汽车行驶路程s为20km时,所花的时间t是多少分钟?
(3)从表中说出随着t逐渐变大,s的变化趋势是什么?
(4)如果汽车行驶的时间为t(min),行驶的路程为s(km),那么路程s与时间t之间的关系式为
.
(5)按照这一行驶规律,当所花的时间t是300min时,汽车行驶的路程s是多少千米?
18.为了解某种品牌小汽车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表:
汽车行驶时间t(h)
0
1
2
3
…
油箱剩余油量Q(L)
100
94
88
82
…
(1)根据上表的数据,请你写出Q与t的关系式;
(2)汽车行驶5h后,油箱中的剩余油量是多少?
(3)该品牌汽车的油箱加50L,若以100km/h的速度匀速行驶,该车最多能行驶多远?
19.一个长方形的宽为xcm,长为ycm,面积为24cm2.
(1)求y与x之间的函数关系式;
(2)当x=8时,长方形的长为多少cm.
20.为了加强公民的节水意识,某地规定用水收费标准如下:每户每月用水量不超过6m3时,水费按每立方米1.1元收费,超过6m3时,超过部分每立方米按1.6元收费,设每户每月用水量为xm3,应缴水费为y元.
(1)写出y与x之间的函数表达式;
(2)如果有两户家庭某月份需缴纳水费为5.5元和9.8元时,求这两户家庭这个月的用水量分别是多少?
21.A、B两地相距90km,甲、乙两人从两地出发相向而行,甲先出发.图中l1,l2表示两人离A地的距离S(km)与时间t(h)的关系,结合图象回答下列问题:
(1)表示甲离A地的距离与时间关系的图象是
(填l1或l2);
甲的速度是
km/h;乙的速度是
km/h.
(2)甲出发后多少时间两人恰好相距15km?
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、y随x的增加而增加,x是自变量,y是因变量,故A选项正确;
B、物体质量每增加1kg,弹簧长度y增加0.5cm,故B选项正确;
C、y与x的关系表达式是y=0.5x+10,故C选项错误;
D、由C知,则当x=7时,y=13.5,即所挂物体质量为7kg时,弹簧长度为13.5cm,故D选项正确;
故选:C.
2.解:C点所有的情况如图所示:
故选:C.
3.解:如图,连接DE,∵△PC′D是△PCD沿PD折叠得到,
∴∠CPD=∠C′PD,
∵PE平分∠BPC′,
∴∠BPE=∠C′PE,
∴∠EPC′+∠DPC′=×180°=90°,
∴△DPE是直角三角形,
∵BP=x,BE=y,AB=3,BC=5,
∴AE=AB﹣BE=3﹣y,CP=BC﹣BP=5﹣x,
在Rt△BEP中,PE2=BP2+BE2=x2+y2,
在Rt△ADE中,DE2=AE2+AD2=(3﹣y)2+52,
在Rt△PCD中,PD2=PC2+CD2=(5﹣x)2+32,
在Rt△PDE中,DE2=PE2+PD2,
则(3﹣y)2+52=x2+y2+(5﹣x)2+32,
整理得,﹣6y=2x2﹣10x,
所以y=﹣x2+x(0<x<5),
纵观各选项,只有D选项符合.
故选:D.
4.解:由题意得,2﹣x≥0且x﹣3≠0,
解答x≤2且x≠3,
所以,自变量x的取值范围是x≤2.
故选:A.
5.解:∵x=≥1
∴x=应代入y=x+5,得y=
故选:A.
6.解:∵小刘家距学校3千米,
∴离校的距离随着时间的增大而增大,
∵路过鲜花店为过生日的妈妈选购了一束鲜花,
∴中间有一段离家的距离不再增大,离校50分钟后离校的距离最大,即3千米.
综合以上C符合,
故选:C.
7.解:当行驶里程x≥8时,设y=kx+b,
将(8,12)、(11,18)代入,
得:,
解得:,
∴y=2x﹣4,
当x=22时,y=2×22﹣4=40,
∴如果小明某次打车行驶里程为22千米,则他的打车费用为40元;
故选:C.
8.解:∵点B(3,5),点E(4,20),点C是BE的中点,
∴点C(,),
∴交易时间在3.5h时累计卖出的数量为12.5万手,故A选项不合题意;
∵直线OB过点(0,0),点B(3,5),
∴直线OB解析式为:y=x,
∵直线AC过点(1,0),点C(,),
∴直线AC解析式为:y=5x﹣5,
联立方程组可得,
∴
∴交易时间在1.5h时累计卖出和累计买入的数量相等,故B选项不合题意;
由图象可得累计卖出的数量和累计买入的数量相差1万手的时刻有4个,故C选项不合题意,
由图象可得从点A对应的时刻到点C对应的时刻,实线在虚线的上方,即平均每小时累计卖出的数量小于买入的数量,故D选项符合题意,
故选:D.
9.解:A、李师傅上班处距他家2000米,此选项错误;
B、李师傅路上耗时20分钟,此选项正确;
C、修车后李师傅骑车速度是=200米/分钟,修车前速度为=100米/分钟,
∴修车后李师傅骑车速度是修车前的2倍,此选项正确;
D、李师傅修车用了5分钟,此选项正确;
故选:A.
10.解:当点Q在AD上运动时,0≤x≤1,
y=?AP?AQ=?x?2x=x2;
当点Q在CD上运动时,1<x≤3,
y=?AP?AD=?x?2=x;
当点Q在CB上运动时,3<x≤4,
y=?AP?CB=?x?(8﹣2x)=﹣x2+4x,
故选:A.
二.填空题(共6小题,满分24分,每小题4分)
11.解:在男子1000米的长跑中,运动员的平均速度v=,则这个关系式中自变量是t,
故答案为:t.
12.解:①、根据图象可知,在40~60分钟,路程没有发生变化,所以小明中途休息的时间为:60﹣40=20分钟,故正确;
②、根据图象可知,当t=40时,s=2800,所以小明休息前爬山的平均速度为:2800÷40=70(米/分钟),故B正确;
③、根据图象可知,小明在上述过程中所走的路程为3800米,故错误;
④、小明休息后的爬山的平均速度为:(3800﹣2800)÷(100﹣60)=25(米/分),小明休息前爬山的平均速度为:2800÷40=70(米/分钟),
70>25,所以小明休息前爬山的平均速度大于休息后爬山的平均速度,故正确;
综上所述,正确的有①②④.
故答案为:①②④
13.解:根据题意得:x+5≠0,
解得:x≠﹣5.
故答案为:x≠﹣5.
14.解:由题意知付款460元,实际标价为460或460×=575(元),
付款560元,实际标价为560×=700(元),
如果一次购买标价460+700=1160(元)的商品应付款
800×0.8+(1160﹣800)×0.6=856(元).
如果一次购买标价575+700=1275(元)的商品应付款
800×0.8+(1275﹣800)×0.6=925(元).
故答案是:856或925.
15.解:根据题意得:
①当0<x≤3时,y=6;
②当x>3时,y=6+1.6(x﹣3)=1.6x+1.2;
∴车费y(元)与路程x(千米)之间的函数关系式为:y=.
故答案为:y=.
16.解:∵运动时间为x秒,△PAB的面积为y
∴观察图象可得,当点P到达点C时,y=4,x=2
∴×AB×2=4
∴AB=4
故①正确;
由函数图象可知,当0≤x≤2时,y=2x,当2<x≤4时,y=4
故②错误;
如图,连接AC,CF,AF
由图可知,AD=BC=2,CG=2,DE=GF=2
∴AE=2+2=4,EF=4﹣2=2
在Rt△AEF中,由勾股定理得:
AF==2
∴③错误;④正确;
∵S△ACF=S△ADC+S正方形DEFG+S△GCF﹣S△AEF
=×4×2+2×2+×2×2﹣×4×2
=4+4+2﹣4
=6
∴⑤正确;
故答案为:①④⑤.
三.解答题(共5小题,满分46分)
17.解:(1)自变量是时间,因变量是路程;
(2)∵当t=1时,s=2,
∴v===2,
∴t==10分钟;
(3)由表得,随着t逐渐变大,s逐渐变大(或者时间每增加1分钟,路程增加2千米);
(4)由(2)得v=2,
∴路程s与时间t之间的关系式为s=2t,
故答案为s=2t;
(5)把t=300代入s=2t,
得s=600.
18.解:(1)Q=100﹣6t;
(2)当t=5时,Q=100﹣6×5=70.
答:汽车行驶5h后,油箱中的剩余油量是70L;
(3)当Q=50时,50=100﹣6t,
6t=50,
解得:t=,
100×=km.
答:该车最多能行驶km.
19.解:(1)由题意可知:y=(x>0)
(2)当x=8时,
y==3
20.解:(1)由题意可得,
当0≤x≤6时,y=1.1x,
当x>6时,y=1.1×6+(x﹣6)×1.6=1.6x﹣3,
即y与x之间的函数表达式是y=;
(2)∵5.5<1.1×6,
∴缴纳水费为5.5元的用户用水量不超过6m3,
将y=5.5代入y=1.1x,解得x=5;
∵9.8>1.1×6,
∴缴纳水费为9.8元的用户用水量超过6m3,
将y=9.8代入y=1.6x﹣3,解得x=8;
答:这两户家庭这个月的用水量分别是5m3,8m3.
21.解:(1)∵甲先出发,
∴表示甲离A地的距离与时间关系的图象是l1,
甲的速度是:90÷2=45km/h,乙的速度是:90÷(3.5﹣0.5)=90÷3=30km/h,
故答案为:l1,45,30;
(2)设甲对应的函数解析式为y=ax+b,
,得,
∴甲对应的函数解析式为y=﹣45x+90,
设乙对应的函数解析式为y=cx+d,
,得,
即乙对应的函数解析式为y=30x﹣15,
∴|(﹣45x+90)﹣(30x﹣15)|=15,
解得,x1=1.2,x2=1.6,
答:甲出发后1.2h或1.6h时两人恰好相距15km.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
