7.2 万有引力定律—【新教材】人教版(2019)高中物理必修第二册课件19张PPT
文档属性
| 名称 | 7.2 万有引力定律—【新教材】人教版(2019)高中物理必修第二册课件19张PPT |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-06 00:00:00 | ||
图片预览






文档简介
第七章 万有引力与宇宙航行
第2节 万有引力定律
1.知道太阳与行星间存在引力。能利用开普勒第三定律和牛顿第三定律推导出太
阳与行星之间的引力表达式。认识物理模型和数学工具在物理学发展过程中的作
用。
2.掌握万有引力定律的内容、含义及适用条件,知道引力常量。
3.认识万有引力的普遍性,能应用万有引力定律解决实际问题。
学科素养目标
各行星都围绕着太阳运行,说明太阳
与行星之间的引力是使行星如此运动的主
要原因。引力的大小和方向能确定吗?
“哥白尼”
探索之路
胡克
胡克等人认为,行星绕太阳运动是因为受到了太阳对它的引力,甚至证明了如果行星的轨道是圆形的,它所受引力的大小跟行星到太阳距离的二次方成反比。但是由于关于运动和力的清晰概念是由牛顿建立的,当时没有这些概念,因此他们无法深入研究。
哥白尼、第谷、开普勒这些科学家不畏艰辛、几十年如一日刻苦专研的精神是成功的基石,值得我们学习。
伽利略
笛卡尔
开普勒
一、行星与太阳间的引力
太阳
行星
r
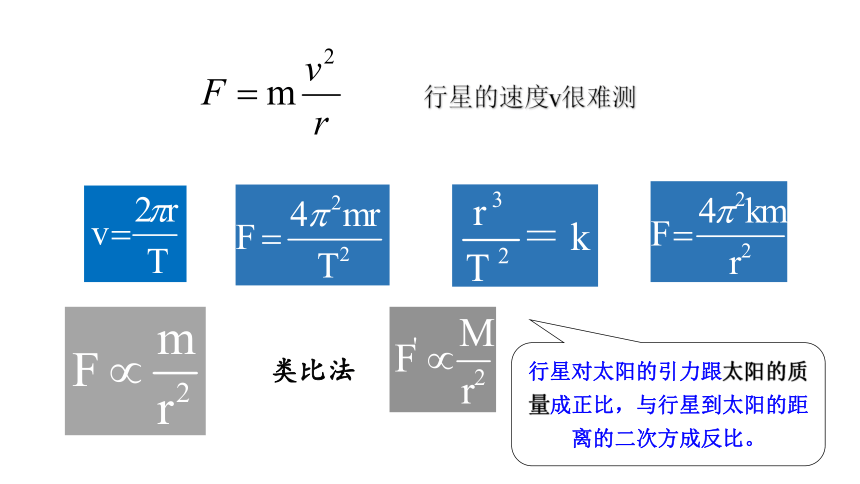
思考:行星的实际运动可以近似看作匀速圆周运动,行星做圆周运动的向心力由什么提供呢?
设行星的质量为m,速度为v,行星到太阳的距离为r,则太阳对行星的引力来提供行星绕太阳做匀速圆周运动所需的向心力:
行星的速度v很难测
类比法
行星对太阳的引力跟太阳的质量成正比,与行星到太阳的距离的二次方成反比。
概括起来
太阳与行星间的引力
表达式
方向:沿着太阳和行星的连线
G为比例系数,与太阳、行星的质量无关。
苹果(物体)
地球(行星)
月球(卫星)
太阳(恒星)
?
是否所有物体之间都存在相互吸引的力呢?
牛顿提出了
“万有引力定律”
?它们受到的引力是否是同一性质的力呢?
“月-地检验”
二、月—地检验
由于月球与地球中心的距离r约
为地球半径R的60倍
已知自由落体加速度g为9.8m/s?,月球中心距离地球中心的距离为3.8×108m,月球公转周期为27.3d,约2.36×106s。根据这些数据,能否验证前面的假设?
结论:月球绕地球运动的力以及地面物体所受地球的引力和太阳与行星之间的力遵循同一规律。
三、万有引力定律
1.内容:自然界中任何两个物体都是互相吸引的,引力的大小跟这两个物体的质量的乘积成正比,跟它们的距离的二次方成反比。
2、数学表达式:
3、适用条件:
(1) 质点
(2)质量分布均匀的球体
r:两质点间的距离
r:两球心间的距离
四、引力常量
卡文迪许实验室
实验数据:
G=6.67×10-11 N·m2/kg2
r
F
r
F
m
m?
m
m?
例题
两个质量分布均匀、密度相同且大小相同的实心小球紧靠在一起,它们之间的万有引力为F。现将其中一个小球中挖去半径为原球半径一半的球,并按如图所示的形式紧靠在一起,三个球心在一条直线上,试计算它们之间的万有引力大小。
解析 如图甲所示,原来是两个实心小球,它们之间的万有引力为F=G??①
从右边的球体中挖去一小球体后,设剩余部分与左边球体之间的万有引力为F'。挖
掉小球体后的右球质量分布不均匀,且不能看成质点,则不能直接应用万有引力定
律求F'的值,可以用“割补法”处理该问题。
左球与挖掉小球体后的右球(图乙)间的万有引力F'等于原来两实心小球间的万有
引力F(图甲)与左球和挖去的小球体间万有引力F1(图丙)之差。F1=G??②
且m1∶m=?∶r3=1∶8?③
联立①②③式得F1=?F
左球与右球剩余部分之间的万有引力大小
F'=F-F1=?F
答案?????F
五、重力和万有引力间的大小关系
重力为地球对物体的万有引力的一个分力。如图所示,设地球的质量为M,半
径为R,A处物体的质量为m,则物体受到地球的万有引力为F,方向指向地心O,由万
有引力公式得F=G。
图中F1为物体随地球自转所需的向心力,F2就是物体的重力mg。故除地球两极外,
重力与纬度的关系
(1)在赤道上,mg=G?-mRω2(物体受万有引力和地面对物体的支持力FN的作用,其
合力充当向心力。FN的大小等于物体重力的大小,ω为地球自转的角速度)。
(2)在地球两极处,由于F向=0,故mg=G?。
(3)在地球上其他位置,重力mg近似处理
一般情况下,重力小于地球对物体的万有引力,但两者差距很小,近似计算中可以认
为物体的重力等于地球对它的万有引力。
(1)在地球表面:mg=G? →g=?,g为重力加速度。
(2)在距地面高h处:mg'=G? →g'=?,高度h越大,重力加速度g'越小。
第2节 万有引力定律
1.知道太阳与行星间存在引力。能利用开普勒第三定律和牛顿第三定律推导出太
阳与行星之间的引力表达式。认识物理模型和数学工具在物理学发展过程中的作
用。
2.掌握万有引力定律的内容、含义及适用条件,知道引力常量。
3.认识万有引力的普遍性,能应用万有引力定律解决实际问题。
学科素养目标
各行星都围绕着太阳运行,说明太阳
与行星之间的引力是使行星如此运动的主
要原因。引力的大小和方向能确定吗?
“哥白尼”
探索之路
胡克
胡克等人认为,行星绕太阳运动是因为受到了太阳对它的引力,甚至证明了如果行星的轨道是圆形的,它所受引力的大小跟行星到太阳距离的二次方成反比。但是由于关于运动和力的清晰概念是由牛顿建立的,当时没有这些概念,因此他们无法深入研究。
哥白尼、第谷、开普勒这些科学家不畏艰辛、几十年如一日刻苦专研的精神是成功的基石,值得我们学习。
伽利略
笛卡尔
开普勒
一、行星与太阳间的引力
太阳
行星
r
思考:行星的实际运动可以近似看作匀速圆周运动,行星做圆周运动的向心力由什么提供呢?
设行星的质量为m,速度为v,行星到太阳的距离为r,则太阳对行星的引力来提供行星绕太阳做匀速圆周运动所需的向心力:
行星的速度v很难测
类比法
行星对太阳的引力跟太阳的质量成正比,与行星到太阳的距离的二次方成反比。
概括起来
太阳与行星间的引力
表达式
方向:沿着太阳和行星的连线
G为比例系数,与太阳、行星的质量无关。
苹果(物体)
地球(行星)
月球(卫星)
太阳(恒星)
?
是否所有物体之间都存在相互吸引的力呢?
牛顿提出了
“万有引力定律”
?它们受到的引力是否是同一性质的力呢?
“月-地检验”
二、月—地检验
由于月球与地球中心的距离r约
为地球半径R的60倍
已知自由落体加速度g为9.8m/s?,月球中心距离地球中心的距离为3.8×108m,月球公转周期为27.3d,约2.36×106s。根据这些数据,能否验证前面的假设?
结论:月球绕地球运动的力以及地面物体所受地球的引力和太阳与行星之间的力遵循同一规律。
三、万有引力定律
1.内容:自然界中任何两个物体都是互相吸引的,引力的大小跟这两个物体的质量的乘积成正比,跟它们的距离的二次方成反比。
2、数学表达式:
3、适用条件:
(1) 质点
(2)质量分布均匀的球体
r:两质点间的距离
r:两球心间的距离
四、引力常量
卡文迪许实验室
实验数据:
G=6.67×10-11 N·m2/kg2
r
F
r
F
m
m?
m
m?
例题
两个质量分布均匀、密度相同且大小相同的实心小球紧靠在一起,它们之间的万有引力为F。现将其中一个小球中挖去半径为原球半径一半的球,并按如图所示的形式紧靠在一起,三个球心在一条直线上,试计算它们之间的万有引力大小。
解析 如图甲所示,原来是两个实心小球,它们之间的万有引力为F=G??①
从右边的球体中挖去一小球体后,设剩余部分与左边球体之间的万有引力为F'。挖
掉小球体后的右球质量分布不均匀,且不能看成质点,则不能直接应用万有引力定
律求F'的值,可以用“割补法”处理该问题。
左球与挖掉小球体后的右球(图乙)间的万有引力F'等于原来两实心小球间的万有
引力F(图甲)与左球和挖去的小球体间万有引力F1(图丙)之差。F1=G??②
且m1∶m=?∶r3=1∶8?③
联立①②③式得F1=?F
左球与右球剩余部分之间的万有引力大小
F'=F-F1=?F
答案?????F
五、重力和万有引力间的大小关系
重力为地球对物体的万有引力的一个分力。如图所示,设地球的质量为M,半
径为R,A处物体的质量为m,则物体受到地球的万有引力为F,方向指向地心O,由万
有引力公式得F=G。
图中F1为物体随地球自转所需的向心力,F2就是物体的重力mg。故除地球两极外,
重力与纬度的关系
(1)在赤道上,mg=G?-mRω2(物体受万有引力和地面对物体的支持力FN的作用,其
合力充当向心力。FN的大小等于物体重力的大小,ω为地球自转的角速度)。
(2)在地球两极处,由于F向=0,故mg=G?。
(3)在地球上其他位置,重力mg
一般情况下,重力小于地球对物体的万有引力,但两者差距很小,近似计算中可以认
为物体的重力等于地球对它的万有引力。
(1)在地球表面:mg=G? →g=?,g为重力加速度。
(2)在距地面高h处:mg'=G? →g'=?,高度h越大,重力加速度g'越小。
