四年级上册数学课件-四 三角形的内角和 青岛版(五四学制)共23张
文档属性
| 名称 | 四年级上册数学课件-四 三角形的内角和 青岛版(五四学制)共23张 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-07 00:00:00 | ||
图片预览





文档简介
三角形的内角和
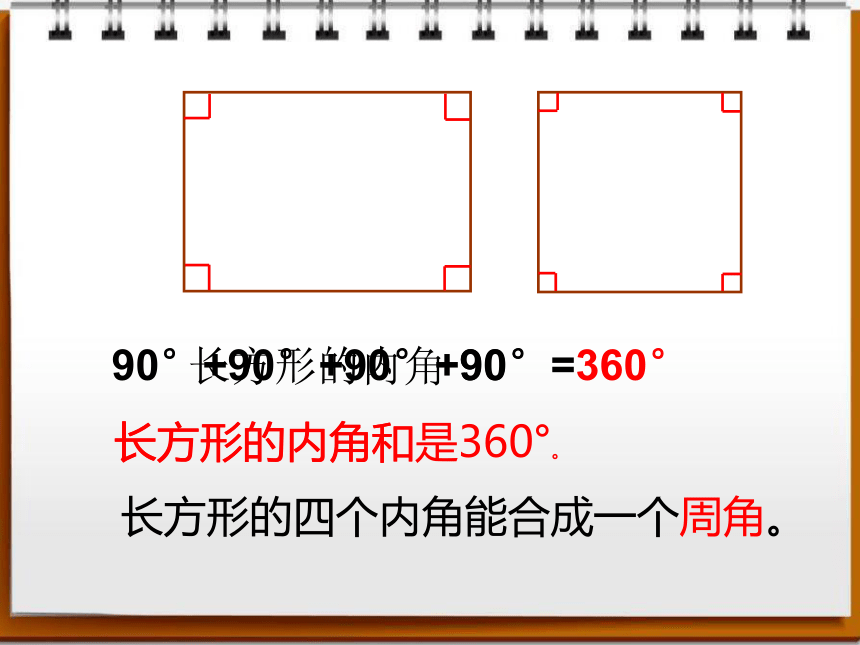
90°
90°+90°+90°+90°=360°
长方形的四个内角能合成一个周角。
长方形的内角和
长方形的内角
长方形的内角和是360°。
小组活动提示:
1.先独立思考,再小组内交流想法。
2. 可以用量一量、撕一撕、折一折等方法探究。
3.把探究过程和结果填写在探究卡上。
帕斯卡
BlaisePascal
(1623~1662) ,
法国数学家、物理学家。
。
。
。
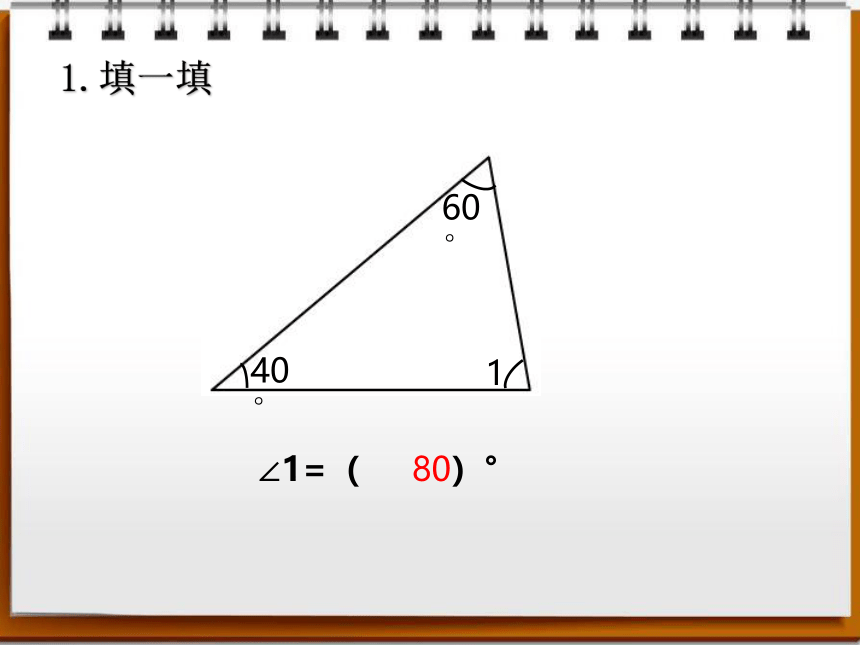
1.填一填
40°
60°
1
∠1=( )°
80
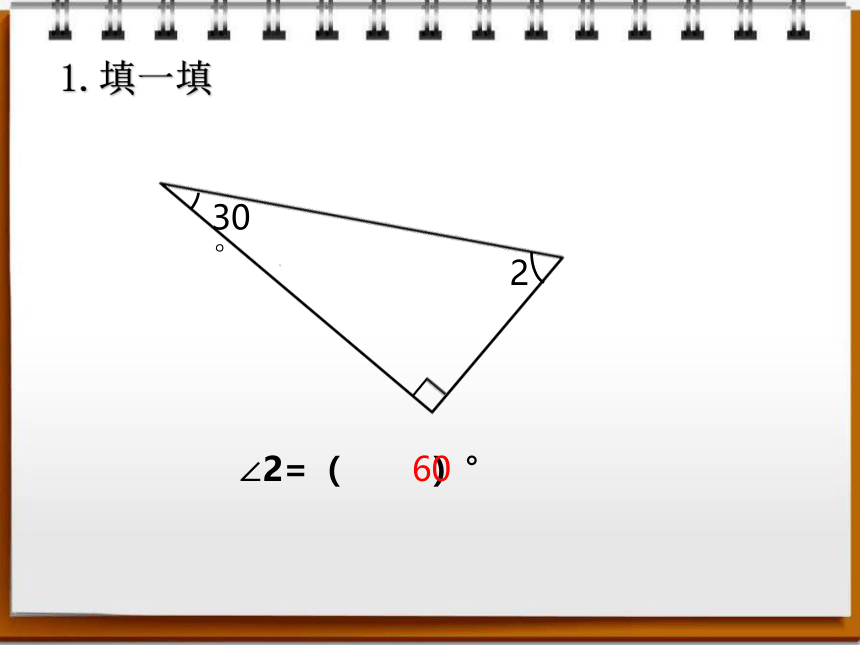
30°
2
∠2=( )°
60
1.填一填
100°
这个等腰三角形的顶角是100°,它的底角是( )°
40
1.填一填
1.填一填
这个等边三角形的每个内角是( )°
60
一个等腰三角形的风筝,它的一个底角是70°,它的顶角是多少度?
180°- 70°-70°
= 110°-70°
=40°
180°-(70°+70°)
=180°-140°
= 40°
?
答:它的顶角是40°。
2.算一算
3.选一选
这本是一块三角形的玻璃,可是被打碎了,
请问它原来是一个( )三角形。
①锐角三角形 ②直角三角形 ③钝角三角形
这本是一块三角形的玻璃,可是被打碎了,
请问它原来是一个( )三角形。
①锐角三角形 ②直角三角形 ③钝角三角形
③
3.选一选
4.画一画
撕拼
量算
折拼
推理
猜想
验证
结论
三角形的内角和?
三角形的内角和是180°。
徐光启
明代科学家
欧几里得
古希腊数学家
在三直線界中之形為三邊形。
在多直線界中之形為多邊形。
在四直線界中之形為四邊形。
五邊以上俱是。
三邊形
三邊線等,為平邊三角形。
有兩邊線等,為兩邊等三角形。
三邊線俱不等,為三不等三角形。
有一鈍角,為三邊鈍角形。
有三銳角,為三邊各銳角形。
有一直角,為三邊直角形。
三邊形
三角形
甲
乙
丙
丁
戊
甲丙戊與乙甲丙等,而戊丙丁與甲乙丙又等,則甲丙丁外角與內兩角甲、乙並等矣。後解曰:甲、乙、丙三角並,與兩直角等。
凡第一形當兩直角,第二形當四直角,第三形當六直角,自此以上,至于無窮。每命形之數倍之,為所當直角之數。又視每形邊數減二邊,即所存變數是本形之數。
一
二
三
四
平面图形
边数
相当于△个数
内角和
3
1
180°
4
2
360°
5
3
6
4
……
……
……
……
90°
90°+90°+90°+90°=360°
长方形的四个内角能合成一个周角。
长方形的内角和
长方形的内角
长方形的内角和是360°。
小组活动提示:
1.先独立思考,再小组内交流想法。
2. 可以用量一量、撕一撕、折一折等方法探究。
3.把探究过程和结果填写在探究卡上。
帕斯卡
BlaisePascal
(1623~1662) ,
法国数学家、物理学家。
。
。
。
1.填一填
40°
60°
1
∠1=( )°
80
30°
2
∠2=( )°
60
1.填一填
100°
这个等腰三角形的顶角是100°,它的底角是( )°
40
1.填一填
1.填一填
这个等边三角形的每个内角是( )°
60
一个等腰三角形的风筝,它的一个底角是70°,它的顶角是多少度?
180°- 70°-70°
= 110°-70°
=40°
180°-(70°+70°)
=180°-140°
= 40°
?
答:它的顶角是40°。
2.算一算
3.选一选
这本是一块三角形的玻璃,可是被打碎了,
请问它原来是一个( )三角形。
①锐角三角形 ②直角三角形 ③钝角三角形
这本是一块三角形的玻璃,可是被打碎了,
请问它原来是一个( )三角形。
①锐角三角形 ②直角三角形 ③钝角三角形
③
3.选一选
4.画一画
撕拼
量算
折拼
推理
猜想
验证
结论
三角形的内角和?
三角形的内角和是180°。
徐光启
明代科学家
欧几里得
古希腊数学家
在三直線界中之形為三邊形。
在多直線界中之形為多邊形。
在四直線界中之形為四邊形。
五邊以上俱是。
三邊形
三邊線等,為平邊三角形。
有兩邊線等,為兩邊等三角形。
三邊線俱不等,為三不等三角形。
有一鈍角,為三邊鈍角形。
有三銳角,為三邊各銳角形。
有一直角,為三邊直角形。
三邊形
三角形
甲
乙
丙
丁
戊
甲丙戊與乙甲丙等,而戊丙丁與甲乙丙又等,則甲丙丁外角與內兩角甲、乙並等矣。後解曰:甲、乙、丙三角並,與兩直角等。
凡第一形當兩直角,第二形當四直角,第三形當六直角,自此以上,至于無窮。每命形之數倍之,為所當直角之數。又視每形邊數減二邊,即所存變數是本形之數。
一
二
三
四
平面图形
边数
相当于△个数
内角和
3
1
180°
4
2
360°
5
3
6
4
……
……
……
……
