5.2比较线段的长短 课件(共27张PPT)
文档属性
| 名称 | 5.2比较线段的长短 课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 16:58:49 | ||
图片预览





文档简介
第五章 基本平面图形
2 比较线段的长短
知识点一 线段的基本性质
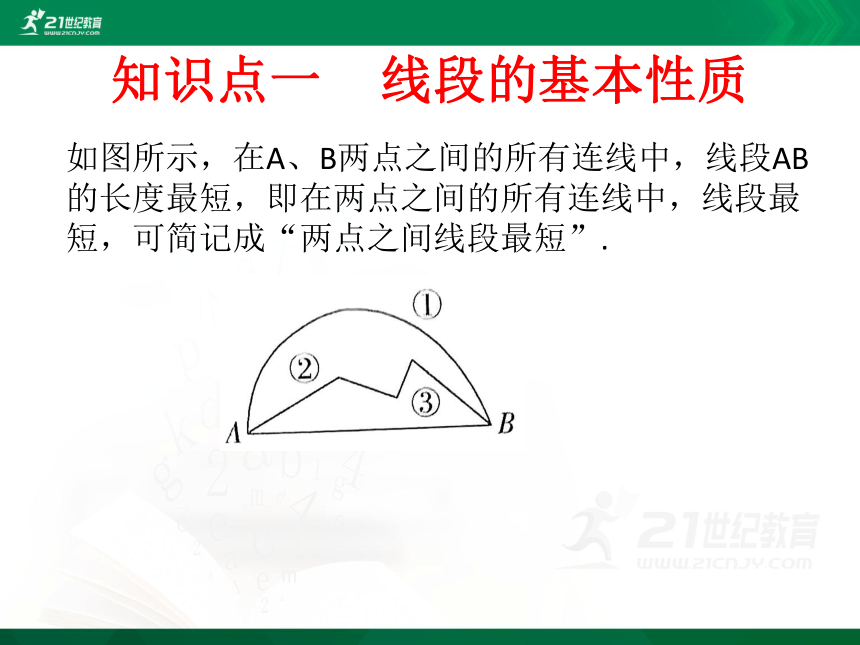
如图所示,在A、B两点之间的所有连线中,线段AB的长度最短,即在两点之间的所有连线中,线段最短,可简记成“两点之间线段最短”.
知识点一 线段的基本性质
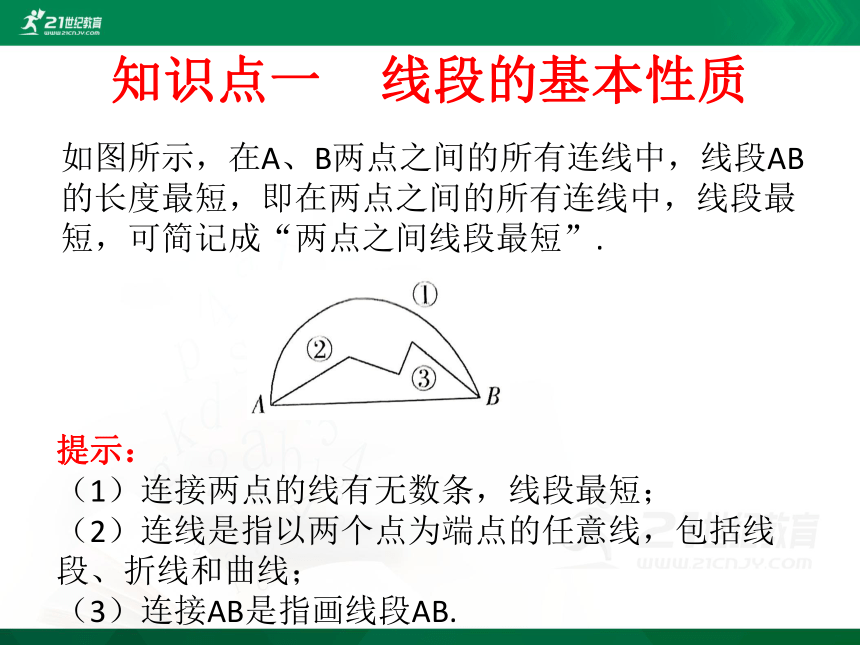
如图所示,在A、B两点之间的所有连线中,线段AB的长度最短,即在两点之间的所有连线中,线段最短,可简记成“两点之间线段最短”.
提示:
(1)连接两点的线有无数条,线段最短;
(2)连线是指以两个点为端点的任意线,包括线段、折线和曲线;
(3)连接AB是指画线段AB.
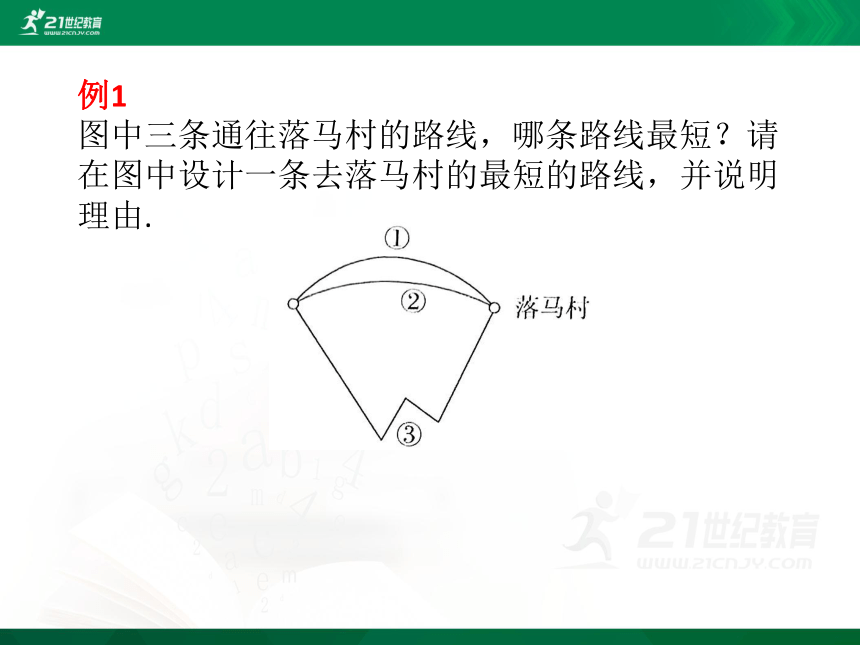
例1
图中三条通往落马村的路线,哪条路线最短?请在图中设计一条去落马村的最短的路线,并说明理由.
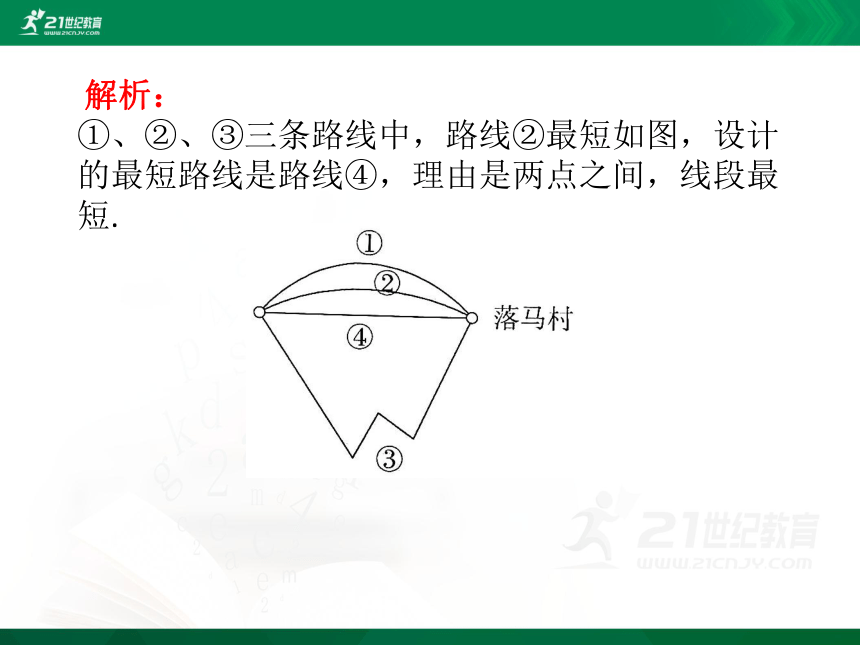
解析:
①、②、③三条路线中,路线②最短如图,设计的最短路线是路线④,理由是两点之间,线段最短.
知识点二 两点之间的距离
连接两点的线段的长度叫做这两点之间的距离.
知识点二 两点之间的距离
连接两点的线段的长度叫做这两点之间的距离.
提示:
(1)“线段”是图形,可以画出来;“距离”是指连接两点的线段的长度,可以量出来,是数量,不是线段本身.
(2)我们通常用刻度尺度量线段的长度.
例2
如图,小亮家、学校和超市在一条直线上,小亮家距离学校2 km,学校距离超市1 km,那么小亮家到超市的距离为___________.
例2
如图,小亮家、学校和超市在一条直线上,小亮家距离学校2 km,学校距离超市1 km,那么小亮家到超市的距离为___________.
解析
小亮家到超市的距离为2+1=3(km).
答案 3 km
知识点三 比较线段的长短
比较线段的长短
度量法
叠合法
用刻度尺量出线段的长度,再进行比较(注意单位要统一)
把其中的一条线段移到另一条线段上,将其中的一个端点重合在一起,使另一个端点分别在重合点的同侧,再进行比较
比较的结果
线段AB与CD比较后,有下列三种结果:AB=CD,AB>CD,AB<CD
例3
比较图中各线段的长短.
例3
比较图中各线段的长短.
解析 线段AC<线段BC<线段AB
点拨 解答这类问题,可以利用叠合法,也可以利用度量法.
知识点四 线段的和、差及尺规作图
1.线段的和差:如图所示,点B在线段AC上,AB=a,BC=b,AC=c,则线段AC可表示为线段AB与BC的和,即AC=AB+BC(或c=a+b);BC可表示为线段AC与AB的差,即BC=AC-AB(或b=c-a);AB可表示为线段AC与BC的差,即AB=AC-BC(或a=c-b).
2.尺规作图的定义:仅用圆规和没有刻度的直尺作图的方法叫做尺规作图.
例4
如图,已知线段a和b,用尺规作一条线段使其长度等于3a+b.
解析
作法:
(1)作射线AN;
(2)在射线AN上顺次截取AB=BC=CD=a;
(3)在射线DN上截取DE=b.
如图所示点拨,线段AE即为所求作的线段.
知识点五 线段的中点
线段的中点
内容
图例
把一条线段分成两条相等线段的点,叫做这条线段的中点
点M是线段AB的中点,AM=BM= AB,即AB=2AM=2BM
注意
(1)一条线段的中点一定在这条线段上;
(2)一条线段只有一个中点.
例5
如图所示,C、D是线段AB上的两点,若AB=10cm,BC=4cm,且D是线段AC的中点,求线段BD的长.
解析
因为AB=10cm,BC=4cm,所以AC=AB-BC=10-4=6cm.因为D是线段AC的中点,所以CD=AC= ×6=3cm.所以BD=BC+CD=4+3=7cm.
点拨
本题在线段和差的基础上,加入了中点的知识,解题的关键是根据条件将待求线段拆开成与已知(或可计算)线段成和差或者倍分的关系的线段.
经典例题
题型一 线段基本事实的应用
例1
如图所示,AB+CD________AC+BD.
(填“<”“>或“=”)
解析
解法一:可以通过度量得出.
解法二:设AC、BD的交点为O,由“两点之间线段最短”可得AB<AO+BO,CD<CO+DO,所以AB+CD<AO+BO+CO+DO,即AB+CD<AC+BD.
答案 <
解析
解法一:可以通过度量得出.
解法二:设AC、BD的交点为O,由“两点之间线段最短”可得AB<AO+BO,CD<CO+DO,所以AB+CD<AO+BO+CO+DO,即AB+CD<AC+BD.
答案 <
点拨
利用“两点之间线段最短”解决,为以后学习“三角形的两边之和大于第三边”作铺垫.
题型二 与线段的比有关的计算
例2
如图所示,某立柱AB=6m,底座BD与中段CD的比为2:3,中段CD是上段AC的3倍.求AC,CD,BD的长.
解析
解法一:因为底座BD与中段CD的比为2:3,中段CD是上段AC的3倍,所以BD:CD:AC=2:3:1,因为AB=6m,所以AC=6× =1m,CD=6× =3m,BD=6× =2m.
解法二:因为底座BD与中段CD的比为2:3,中段CD是上段AC的3倍,所以BD:CD:AC=2:3:1,所以设BD=2x m,CD=3x m,AC=x m.因为AB=6 m,所以2x+3x+x=6,所以x=1.所以AC=1m,CD=3m,BD=2m.
解析
解法一:因为底座BD与中段CD的比为2:3,中段CD是上段AC的3倍,所以BD:CD:AC=2:3:1,因为AB=6m,所以AC=6× =1m,CD=6× =3m,BD=6× =2m.
解法二:因为底座BD与中段CD的比为2:3,中段CD是上段AC的3倍,所以BD:CD:AC=2:3:1,所以设BD=2x m,CD=3x m,AC=x m.因为AB=6 m,所以2x+3x+x=6,所以x=1.所以AC=1m,CD=3m,BD=2m.
点拨
这种根据线段的比设出未知数,建立方程解决问题的思想方法,数学中称为方程思想.
易错易混
易错点 忽视“直线”条件而导致漏解
例
已知点B在直线AC上,AB=6,AC=10,点P、Q分别是AB、AC的中点,求PQ的长.
解析
有点B在线段AC上或在线段CA的延长线上两种可能.由点P、Q分别为AB、AC的中点可知
AP=
AB=3,AQ=
AC=5.
如下图所示,当点B在线段AC上时,PQ=AQ-AP=2.
如下图,当点B在线段CA的延长线上时,PQ=AQ+AP=8.
所以PQ的长为2或8.
易错警示:
“无图有陷阱”,时刻要牢记.这是一道典型的数形结合题,用几何的思想、代数的方法进行计算即可.
2 比较线段的长短
知识点一 线段的基本性质
如图所示,在A、B两点之间的所有连线中,线段AB的长度最短,即在两点之间的所有连线中,线段最短,可简记成“两点之间线段最短”.
知识点一 线段的基本性质
如图所示,在A、B两点之间的所有连线中,线段AB的长度最短,即在两点之间的所有连线中,线段最短,可简记成“两点之间线段最短”.
提示:
(1)连接两点的线有无数条,线段最短;
(2)连线是指以两个点为端点的任意线,包括线段、折线和曲线;
(3)连接AB是指画线段AB.
例1
图中三条通往落马村的路线,哪条路线最短?请在图中设计一条去落马村的最短的路线,并说明理由.
解析:
①、②、③三条路线中,路线②最短如图,设计的最短路线是路线④,理由是两点之间,线段最短.
知识点二 两点之间的距离
连接两点的线段的长度叫做这两点之间的距离.
知识点二 两点之间的距离
连接两点的线段的长度叫做这两点之间的距离.
提示:
(1)“线段”是图形,可以画出来;“距离”是指连接两点的线段的长度,可以量出来,是数量,不是线段本身.
(2)我们通常用刻度尺度量线段的长度.
例2
如图,小亮家、学校和超市在一条直线上,小亮家距离学校2 km,学校距离超市1 km,那么小亮家到超市的距离为___________.
例2
如图,小亮家、学校和超市在一条直线上,小亮家距离学校2 km,学校距离超市1 km,那么小亮家到超市的距离为___________.
解析
小亮家到超市的距离为2+1=3(km).
答案 3 km
知识点三 比较线段的长短
比较线段的长短
度量法
叠合法
用刻度尺量出线段的长度,再进行比较(注意单位要统一)
把其中的一条线段移到另一条线段上,将其中的一个端点重合在一起,使另一个端点分别在重合点的同侧,再进行比较
比较的结果
线段AB与CD比较后,有下列三种结果:AB=CD,AB>CD,AB<CD
例3
比较图中各线段的长短.
例3
比较图中各线段的长短.
解析 线段AC<线段BC<线段AB
点拨 解答这类问题,可以利用叠合法,也可以利用度量法.
知识点四 线段的和、差及尺规作图
1.线段的和差:如图所示,点B在线段AC上,AB=a,BC=b,AC=c,则线段AC可表示为线段AB与BC的和,即AC=AB+BC(或c=a+b);BC可表示为线段AC与AB的差,即BC=AC-AB(或b=c-a);AB可表示为线段AC与BC的差,即AB=AC-BC(或a=c-b).
2.尺规作图的定义:仅用圆规和没有刻度的直尺作图的方法叫做尺规作图.
例4
如图,已知线段a和b,用尺规作一条线段使其长度等于3a+b.
解析
作法:
(1)作射线AN;
(2)在射线AN上顺次截取AB=BC=CD=a;
(3)在射线DN上截取DE=b.
如图所示点拨,线段AE即为所求作的线段.
知识点五 线段的中点
线段的中点
内容
图例
把一条线段分成两条相等线段的点,叫做这条线段的中点
点M是线段AB的中点,AM=BM= AB,即AB=2AM=2BM
注意
(1)一条线段的中点一定在这条线段上;
(2)一条线段只有一个中点.
例5
如图所示,C、D是线段AB上的两点,若AB=10cm,BC=4cm,且D是线段AC的中点,求线段BD的长.
解析
因为AB=10cm,BC=4cm,所以AC=AB-BC=10-4=6cm.因为D是线段AC的中点,所以CD=AC= ×6=3cm.所以BD=BC+CD=4+3=7cm.
点拨
本题在线段和差的基础上,加入了中点的知识,解题的关键是根据条件将待求线段拆开成与已知(或可计算)线段成和差或者倍分的关系的线段.
经典例题
题型一 线段基本事实的应用
例1
如图所示,AB+CD________AC+BD.
(填“<”“>或“=”)
解析
解法一:可以通过度量得出.
解法二:设AC、BD的交点为O,由“两点之间线段最短”可得AB<AO+BO,CD<CO+DO,所以AB+CD<AO+BO+CO+DO,即AB+CD<AC+BD.
答案 <
解析
解法一:可以通过度量得出.
解法二:设AC、BD的交点为O,由“两点之间线段最短”可得AB<AO+BO,CD<CO+DO,所以AB+CD<AO+BO+CO+DO,即AB+CD<AC+BD.
答案 <
点拨
利用“两点之间线段最短”解决,为以后学习“三角形的两边之和大于第三边”作铺垫.
题型二 与线段的比有关的计算
例2
如图所示,某立柱AB=6m,底座BD与中段CD的比为2:3,中段CD是上段AC的3倍.求AC,CD,BD的长.
解析
解法一:因为底座BD与中段CD的比为2:3,中段CD是上段AC的3倍,所以BD:CD:AC=2:3:1,因为AB=6m,所以AC=6× =1m,CD=6× =3m,BD=6× =2m.
解法二:因为底座BD与中段CD的比为2:3,中段CD是上段AC的3倍,所以BD:CD:AC=2:3:1,所以设BD=2x m,CD=3x m,AC=x m.因为AB=6 m,所以2x+3x+x=6,所以x=1.所以AC=1m,CD=3m,BD=2m.
解析
解法一:因为底座BD与中段CD的比为2:3,中段CD是上段AC的3倍,所以BD:CD:AC=2:3:1,因为AB=6m,所以AC=6× =1m,CD=6× =3m,BD=6× =2m.
解法二:因为底座BD与中段CD的比为2:3,中段CD是上段AC的3倍,所以BD:CD:AC=2:3:1,所以设BD=2x m,CD=3x m,AC=x m.因为AB=6 m,所以2x+3x+x=6,所以x=1.所以AC=1m,CD=3m,BD=2m.
点拨
这种根据线段的比设出未知数,建立方程解决问题的思想方法,数学中称为方程思想.
易错易混
易错点 忽视“直线”条件而导致漏解
例
已知点B在直线AC上,AB=6,AC=10,点P、Q分别是AB、AC的中点,求PQ的长.
解析
有点B在线段AC上或在线段CA的延长线上两种可能.由点P、Q分别为AB、AC的中点可知
AP=
AB=3,AQ=
AC=5.
如下图所示,当点B在线段AC上时,PQ=AQ-AP=2.
如下图,当点B在线段CA的延长线上时,PQ=AQ+AP=8.
所以PQ的长为2或8.
易错警示:
“无图有陷阱”,时刻要牢记.这是一道典型的数形结合题,用几何的思想、代数的方法进行计算即可.
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
