2.2.4 二次函数y=ax2+bx+c(a≠0)的图象与性质同步练习(含答案)
文档属性
| 名称 | 2.2.4 二次函数y=ax2+bx+c(a≠0)的图象与性质同步练习(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 383.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-07 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2020-2021学年九年级数学下册课时作业(北师版)
第二章 二次函数
2 二次函数的图象与性质
第4课时 二次函数y=ax2+bx+c(a≠0)的图象与性质
一、选择题
1.二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)对应值列表如下:
x … -3 -2 -1 0 1 …
y … -3 -2 -3 -6 -11 …
则该函数图象的对称轴是( )
A.直线x=-3 B.直线x=-2
C.直线x=-1 D.直线x=0
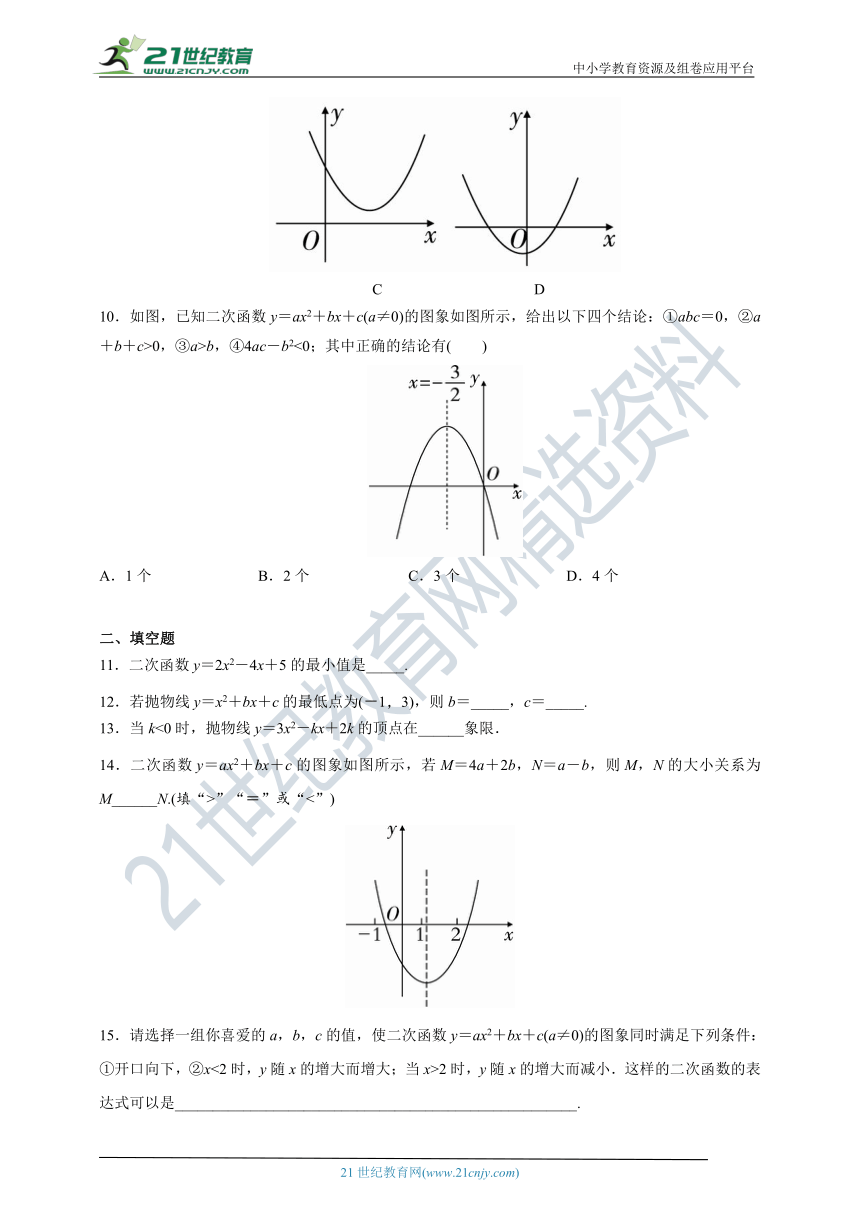
2.二次函数y=ax2+bx+c的图象如图所示,则下列结论中,正确的是( )
A.ab>0,c>0 B.ab>0,c<0
C.ab<0,c>0 D.ab<0,c<0
3.若A(-,y1),B(-1,y2),C(-,y3)为二次函数y=-x2-4x+5的图象上三点,则y1,y2,y3的大小关系是( )
A.y1C.y34.同一坐标系中,二次函数y=ax2+bx+c与一次函数y=ax+c的图象是( )
A B
C D
5.二次函数y=x2-4x+2c2的图象的顶点在x轴上,则c的值为( )
A.2 B.-2 C.- D.±
6.二次函数y=ax2+bx+c中,b2=ac,且x=0时,y=-4,则( )
A.y最大=-3 B.y最小=-3
C.y最大=4 D.y最小=-4
7.在同一平面直角坐标系中,若抛物线y=x2+(2m-1)x+2m-4与y=x2-(3m+n)x+n关于y轴对称,则符合条件的m,n的值为( )
A.m=,n=- B.m=5,n=-6
C.m=-1,n=6 D.m=1,n=-2
8.已知二次函数y=ax2+bx+c(a>0)的图象经过点A(-1,2),B(2,5),顶点坐标为(m,n),则下列说法错误的是( )
A.c<3 B.m> C.n≤2 D.b<1
9.如图,一次函数y1=x与二次函数y2=ax2+bx+c的图象相交于P,Q两点,则函数y=ax2+(b-1)x+c的图象可能是( )
A B
C D
10.如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac-b2<0;其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.二次函数y=2x2-4x+5的最小值是_____.
12.若抛物线y=x2+bx+c的最低点为(-1,3),则b=_____,c=_____.
13.当k<0时,抛物线y=3x2-kx+2k的顶点在______象限.
14.二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b,N=a-b,则M,N的大小关系为M______N.(填“>”“=”或“<”)
15.请选择一组你喜爱的a,b,c的值,使二次函数y=ax2+bx+c(a≠0)的图象同时满足下列条件:①开口向下,②x<2时,y随x的增大而增大;当x>2时,y随x的增大而减小.这样的二次函数的表达式可以是_____________________________________________________.
三、解答题
16.已知抛物线y=ax2+bx+c如图所示,对称轴x=-1.
(1)确定a,b,c的符号;
(2)求证:a-b+c>0;
(3)当x为何值时,y>0?当x为何值时,y<0?当x为何值时,y=0?
17.若两个二次函数图象的顶点相同,开口大小相同,但开口方向相反,则称这两个二次函数为“对称二次函数”.
(1)请写出二次函数y=2(x-2)2+1的“对称二次函数”;
(2)已知关于x的二次函数y1=x2-3x+1和y2=ax2+bx+c,若y1-y2与y1互为“对称二次函数”,求函数y2的表达式,并求出当-3≤x≤3时,y2的最大值.
18.已知函数y=x2+bx+c(b,c为常数)的图象经过点(-2,4).
(1)求b,c满足的关系式;
(2)设该函数图象的顶点坐标是(m,n),当b的值变化时,求n关于m的函数解析式;
(3)设该函数的图象不经过第三象限,当-5≤x≤1时,函数的最大值与最小值之差为16,求b的值.
参 考 答 案
1. B 2. C 3. C 4. D 5. D 6. A 7. D 8. B 9. A 10. C
11. 3
12. 2 4
13. 三
14. <
15. y=-x2+4x-3(答案不唯一,只要满足对称轴是x=2,a<0即可)
16. 解:(1)∵抛物线的开口向下,∴a<0.∵对称轴为x=-1,∴-<0.又∵a<0,∴b<0.∵抛物线交y轴于正半轴,∴c>0.
(2)x=-1时,y=a-b+c,而由图象知,x=-1时,y>0,∴a-b+c>0.
(3)根据图象,当-3<x<1时,y>0,当x<-3或x>1时,y<0,当x=-3或1时,y=0.
17. 解:(1)二次函数y=2(x-2)2+1的对称二次函数是y=-2(x-2)2+1.
(2)∵y1=x2-3x+1,y2=ax2+bx+c,∴y1-y2=(1-a)x2-(3+b)x+1-c=(1-a)·[x-]2+.又∵y1-y2与y1互为“对称二次函数”,y1=x2-3x+1=(x-)2-,∴ 解得∴y2=2x2-6x+,∴y2=2(x-)2,∴y2的抛物线的对称轴为直线x=,∵a=2>0,且-3≤x≤3,∴当x=-3时,y最大值=2×(-3)2-6×(-3)+=.故函数y2的表达式是y2=2x2-6x+,当x=-3时,y2的最大值是.
18. 解:(1)将点(-2,4)代入y=x2+bx+c中得4=(-2)2-2b+c.∴c=2b.∴b,c满足的关系式是c=2b.
(2)把c=2b代入y=x2+bx+c,得y=x2+bx+2b.∵顶点坐标是(m,n),∴n=m2+bm+2b,且m=-,即b=-2m.∴n=m2+(-2m)m+2×(-2m)=-m2-4m.∴n关于m的函数解析式为n=-m2-4m.
(3)由(2)的结论,画出函数y=x2+bx+c和函数y=-x2-4x的图象如图.∵函数y=x2+bx+c的图象不经过第三象限,∴-4≤-≤0.①当-4≤-≤-2,即4≤b≤8时,如图1所示,x=1时,函数取到最大值y=1+3b;当x=-时,函数取到最小值y=,∴(1+3b)-=16,即b2+4b-60=0.∴b1=6,b2=-10(舍去).
_21?????????è?????(www.21cnjy.com)_
2020-2021学年九年级数学下册课时作业(北师版)
第二章 二次函数
2 二次函数的图象与性质
第4课时 二次函数y=ax2+bx+c(a≠0)的图象与性质
一、选择题
1.二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)对应值列表如下:
x … -3 -2 -1 0 1 …
y … -3 -2 -3 -6 -11 …
则该函数图象的对称轴是( )
A.直线x=-3 B.直线x=-2
C.直线x=-1 D.直线x=0
2.二次函数y=ax2+bx+c的图象如图所示,则下列结论中,正确的是( )
A.ab>0,c>0 B.ab>0,c<0
C.ab<0,c>0 D.ab<0,c<0
3.若A(-,y1),B(-1,y2),C(-,y3)为二次函数y=-x2-4x+5的图象上三点,则y1,y2,y3的大小关系是( )
A.y1
A B
C D
5.二次函数y=x2-4x+2c2的图象的顶点在x轴上,则c的值为( )
A.2 B.-2 C.- D.±
6.二次函数y=ax2+bx+c中,b2=ac,且x=0时,y=-4,则( )
A.y最大=-3 B.y最小=-3
C.y最大=4 D.y最小=-4
7.在同一平面直角坐标系中,若抛物线y=x2+(2m-1)x+2m-4与y=x2-(3m+n)x+n关于y轴对称,则符合条件的m,n的值为( )
A.m=,n=- B.m=5,n=-6
C.m=-1,n=6 D.m=1,n=-2
8.已知二次函数y=ax2+bx+c(a>0)的图象经过点A(-1,2),B(2,5),顶点坐标为(m,n),则下列说法错误的是( )
A.c<3 B.m> C.n≤2 D.b<1
9.如图,一次函数y1=x与二次函数y2=ax2+bx+c的图象相交于P,Q两点,则函数y=ax2+(b-1)x+c的图象可能是( )
A B
C D
10.如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac-b2<0;其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.二次函数y=2x2-4x+5的最小值是_____.
12.若抛物线y=x2+bx+c的最低点为(-1,3),则b=_____,c=_____.
13.当k<0时,抛物线y=3x2-kx+2k的顶点在______象限.
14.二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b,N=a-b,则M,N的大小关系为M______N.(填“>”“=”或“<”)
15.请选择一组你喜爱的a,b,c的值,使二次函数y=ax2+bx+c(a≠0)的图象同时满足下列条件:①开口向下,②x<2时,y随x的增大而增大;当x>2时,y随x的增大而减小.这样的二次函数的表达式可以是_____________________________________________________.
三、解答题
16.已知抛物线y=ax2+bx+c如图所示,对称轴x=-1.
(1)确定a,b,c的符号;
(2)求证:a-b+c>0;
(3)当x为何值时,y>0?当x为何值时,y<0?当x为何值时,y=0?
17.若两个二次函数图象的顶点相同,开口大小相同,但开口方向相反,则称这两个二次函数为“对称二次函数”.
(1)请写出二次函数y=2(x-2)2+1的“对称二次函数”;
(2)已知关于x的二次函数y1=x2-3x+1和y2=ax2+bx+c,若y1-y2与y1互为“对称二次函数”,求函数y2的表达式,并求出当-3≤x≤3时,y2的最大值.
18.已知函数y=x2+bx+c(b,c为常数)的图象经过点(-2,4).
(1)求b,c满足的关系式;
(2)设该函数图象的顶点坐标是(m,n),当b的值变化时,求n关于m的函数解析式;
(3)设该函数的图象不经过第三象限,当-5≤x≤1时,函数的最大值与最小值之差为16,求b的值.
参 考 答 案
1. B 2. C 3. C 4. D 5. D 6. A 7. D 8. B 9. A 10. C
11. 3
12. 2 4
13. 三
14. <
15. y=-x2+4x-3(答案不唯一,只要满足对称轴是x=2,a<0即可)
16. 解:(1)∵抛物线的开口向下,∴a<0.∵对称轴为x=-1,∴-<0.又∵a<0,∴b<0.∵抛物线交y轴于正半轴,∴c>0.
(2)x=-1时,y=a-b+c,而由图象知,x=-1时,y>0,∴a-b+c>0.
(3)根据图象,当-3<x<1时,y>0,当x<-3或x>1时,y<0,当x=-3或1时,y=0.
17. 解:(1)二次函数y=2(x-2)2+1的对称二次函数是y=-2(x-2)2+1.
(2)∵y1=x2-3x+1,y2=ax2+bx+c,∴y1-y2=(1-a)x2-(3+b)x+1-c=(1-a)·[x-]2+.又∵y1-y2与y1互为“对称二次函数”,y1=x2-3x+1=(x-)2-,∴ 解得∴y2=2x2-6x+,∴y2=2(x-)2,∴y2的抛物线的对称轴为直线x=,∵a=2>0,且-3≤x≤3,∴当x=-3时,y最大值=2×(-3)2-6×(-3)+=.故函数y2的表达式是y2=2x2-6x+,当x=-3时,y2的最大值是.
18. 解:(1)将点(-2,4)代入y=x2+bx+c中得4=(-2)2-2b+c.∴c=2b.∴b,c满足的关系式是c=2b.
(2)把c=2b代入y=x2+bx+c,得y=x2+bx+2b.∵顶点坐标是(m,n),∴n=m2+bm+2b,且m=-,即b=-2m.∴n=m2+(-2m)m+2×(-2m)=-m2-4m.∴n关于m的函数解析式为n=-m2-4m.
(3)由(2)的结论,画出函数y=x2+bx+c和函数y=-x2-4x的图象如图.∵函数y=x2+bx+c的图象不经过第三象限,∴-4≤-≤0.①当-4≤-≤-2,即4≤b≤8时,如图1所示,x=1时,函数取到最大值y=1+3b;当x=-时,函数取到最小值y=,∴(1+3b)-=16,即b2+4b-60=0.∴b1=6,b2=-10(舍去).
_21?????????è?????(www.21cnjy.com)_
