5.1曲线运动(小船渡河模型)—人教版高中物理必修二课件16张PPT
文档属性
| 名称 | 5.1曲线运动(小船渡河模型)—人教版高中物理必修二课件16张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 599.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-07 00:00:00 | ||
图片预览





文档简介
5.1 曲线运动
(小船渡河模型)
人教版 高中物理必修二
第五章曲线运动
一、小船渡河模型
小船渡河问题是运动的合成与分解的一个典型实例,又是教材中小蜡块实验的拓展与延伸。
2.模型的特点:
①一般情况下,船速和水速恒定,河岸平直且平行。
②船的实际运动是随水流的运动和船相对静水的运动的合运动。
1.模型构建: 匀速运动的船在匀速流动的水中航行,该运动情景可看作“小船渡河”模型。
一、小船渡河模型
3.三个速度 v船(船在静水中的速度)、v水(水流速度)、v合(船的实际速度).
4.求解小船渡河问题有两类:
①求最短渡河时间;②求最短渡河位移。
5.无论哪类都必须明确以几点:
(1)解决这类问题的关键是:正确区分分运动和合运动,船的航行方向也就是船头指向,是分运动。船的运动方向也就是船的实际运动方向,是合运动,一般情况下与船头指向不一致。
一、小船渡河模型
(2)运动分解的基本方法,按实际效果分解,一般用平行四边形定则按水流方向和船头指向分解。
(3)渡河时间只与垂直河岸的船的分速度有关,与水流速度无关。
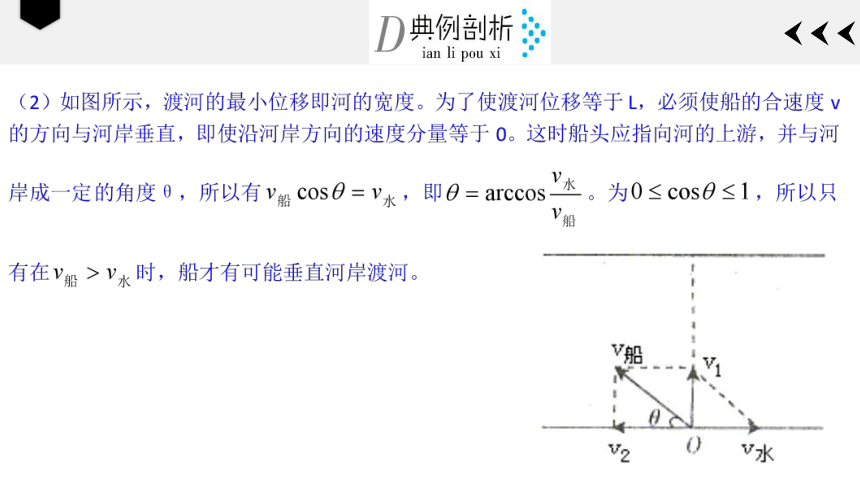
一条宽度为L的河,水流速度为V水,已知船在静水中速度为V船,那么:(1)怎样渡河时间最短?(2)若V船>V水,怎样渡河位移最小?
(3)若V船一、小船渡河模型
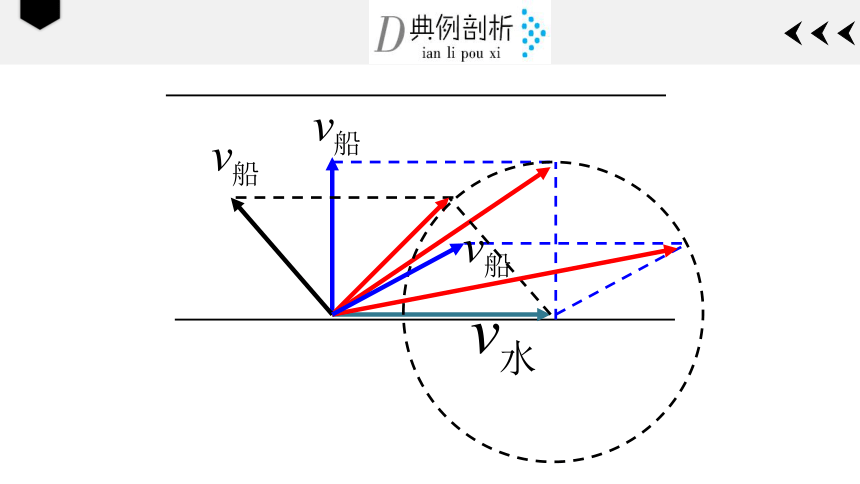
(4)求渡河的航程实际就是求小船实际运动的轨迹长度,其中最短航程为常求的量,一般要分两种情况讨论:
①若v水一、小船渡河模型
针对练习1:(单选题)某小船在静水中的运动大小保持不变,该小船要渡过一条河,渡河时小船船头垂直指向河岸,若船行至河中间时,水流速度突然增大,则( )
A 小船渡河时间不变
B 小船渡河时间减少
C 小船渡河时间增加
D 小船到达对岸地点不变
A
针对练习2:一艘小船在100m宽的河中横渡到对岸,已知水流速度为2m/s,小船在静水中的速度是4m/s,求:
(1)要使船以最短的时间渡到对岸,船头所指方向与河岸间的夹角为多大?船渡到对岸所需最短时间是多少?船发生的位移是多大?
(2)要使船以最短的距离到对岸,船头所指方向与河岸间的夹角多大?船到对岸所需时间是多少?
针对练习3:河宽d=300m ,水流速度为v1=4m/s,船在静水中的速度是v2=3m/s,求:
(1)欲使船渡河时间最短,船应怎样渡河?最短时间是多少?船经过的位移是多大?
(2)欲使船航行距离最短,船应怎样渡河?渡河时间多长?
?
C
课后作业:
完成第五章第一节相关练习
预习“关联速度”相关知识
(小船渡河模型)
人教版 高中物理必修二
第五章曲线运动
一、小船渡河模型
小船渡河问题是运动的合成与分解的一个典型实例,又是教材中小蜡块实验的拓展与延伸。
2.模型的特点:
①一般情况下,船速和水速恒定,河岸平直且平行。
②船的实际运动是随水流的运动和船相对静水的运动的合运动。
1.模型构建: 匀速运动的船在匀速流动的水中航行,该运动情景可看作“小船渡河”模型。
一、小船渡河模型
3.三个速度 v船(船在静水中的速度)、v水(水流速度)、v合(船的实际速度).
4.求解小船渡河问题有两类:
①求最短渡河时间;②求最短渡河位移。
5.无论哪类都必须明确以几点:
(1)解决这类问题的关键是:正确区分分运动和合运动,船的航行方向也就是船头指向,是分运动。船的运动方向也就是船的实际运动方向,是合运动,一般情况下与船头指向不一致。
一、小船渡河模型
(2)运动分解的基本方法,按实际效果分解,一般用平行四边形定则按水流方向和船头指向分解。
(3)渡河时间只与垂直河岸的船的分速度有关,与水流速度无关。
一条宽度为L的河,水流速度为V水,已知船在静水中速度为V船,那么:(1)怎样渡河时间最短?(2)若V船>V水,怎样渡河位移最小?
(3)若V船
(4)求渡河的航程实际就是求小船实际运动的轨迹长度,其中最短航程为常求的量,一般要分两种情况讨论:
①若v水
针对练习1:(单选题)某小船在静水中的运动大小保持不变,该小船要渡过一条河,渡河时小船船头垂直指向河岸,若船行至河中间时,水流速度突然增大,则( )
A 小船渡河时间不变
B 小船渡河时间减少
C 小船渡河时间增加
D 小船到达对岸地点不变
A
针对练习2:一艘小船在100m宽的河中横渡到对岸,已知水流速度为2m/s,小船在静水中的速度是4m/s,求:
(1)要使船以最短的时间渡到对岸,船头所指方向与河岸间的夹角为多大?船渡到对岸所需最短时间是多少?船发生的位移是多大?
(2)要使船以最短的距离到对岸,船头所指方向与河岸间的夹角多大?船到对岸所需时间是多少?
针对练习3:河宽d=300m ,水流速度为v1=4m/s,船在静水中的速度是v2=3m/s,求:
(1)欲使船渡河时间最短,船应怎样渡河?最短时间是多少?船经过的位移是多大?
(2)欲使船航行距离最短,船应怎样渡河?渡河时间多长?
?
C
课后作业:
完成第五章第一节相关练习
预习“关联速度”相关知识
