2020-2021学年上海市浦东新区第四教育署七年级(上)期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年上海市浦东新区第四教育署七年级(上)期末数学试卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 554.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-07 00:00:00 | ||
图片预览




文档简介
2020-2021学年上海市浦东新区第四教育署七年级第一学期期末数学试卷(五四学制)
一、选择题(共6小题).
1.在下列式子:﹣5x,,a2﹣b2,,中,分式有( )
A.1个 B.2个 C.3个 D.4个
2.多项式3x﹣9,x2﹣9与x2﹣6x+9的公因式为( )
A.x+3 B.(x+3)2 C.x﹣3 D.x2+9
3.下列运算中,正确的是( )
A.(﹣m)6÷(﹣m)3=﹣m3 B.(﹣a3)2=﹣a6
C.(xy2)2=xy4 D.a2?a3=a6
4.若a=﹣3﹣2,b=(﹣)﹣2,c=(﹣0.3)0,则a,b,c的大小关系是( )
A.a<b<c B.b<c<a C.c<b<a D.a<c<b
5.若把x,y的值同时扩大为原来的2倍,则下列分式的值保持不变的是( )
A. B. C. D.
6.下列四个汉字是轴对称图形的是( )
A. B. C. D.
二、填空题(共12小题).
7.单项式﹣6x3y的次数是 次.
8.已知7xay2和﹣9x5yb是同类项,则= .
9.当x 时,分式有意义.
10.在括号内填入适当的整式:(2a+b)( )=b2﹣4a2.
11.分解因式:m2+2m﹣3= .
12.计算:(3a6b3﹣6ab5)÷3ab= .
13.计算:= .
14.一种花的花粉颗粒直径约为0.00065米,0.00065用科学记数法表示为 .
15.如果关于x的方程有增根,那么k= .
16.若am=6,an=4,则a2m﹣n= .
17.在正方形、长方形、线段、等边三角形和平行四边形这五种图形中,是旋转对称图形不是中心对称图形的是 .
18.如图,在长方形ABCD中,AB=2cm,BC=3cm,E、F分别是AD、BC的中点,如果将长方形ABFE绕点F顺时针旋转90°,那么旋转后的长方形与长方形CDEF重叠部分的面积是 cm2.
三、解答题(共9小题).
19.计算:a?a7﹣(﹣3a4)2+a10÷a2.
20.ab(a﹣2+b﹣2).(结果只含有正整数指数幂)
21.分解因式:2x3+12x2y+18xy2.
22.因式分解:(x2+2x)2﹣7(x2+2x)﹣8.
23.解分式方程:﹣=1﹣.
24.如图,已知在平面内有三角形ABC和点D,请根据下列要求画出对应的图形,并回答问题.
(1)将△ABC平移,使得点A平移到图中点D的位置,点B、点C的对应点分别为点E、点F,请画出△DEF.
(2)画出△ABC关于点D成中心对称的△A1B1C1.
(3)△DEF与△A1B1C1是否关于某个点成中心对称?如果是,请在图中画出这个对称中心,并记作点O.
25.先化简,再求值:+÷,其中x=3.
26.某中学为配合开展“垃圾分类进校园”活动,新购买了一批不同型号的垃圾分类垃圾桶,学校先用2700元购买了一批给班级使用的小号垃圾桶,再用3600元购买了一批放在户外永久使用的大号垃圾桶,已知每个大号垃圾桶的价格是小号垃圾桶的4倍,且购买的数量比小号垃圾桶少40个,求每个小号垃圾桶的价格是多少元?
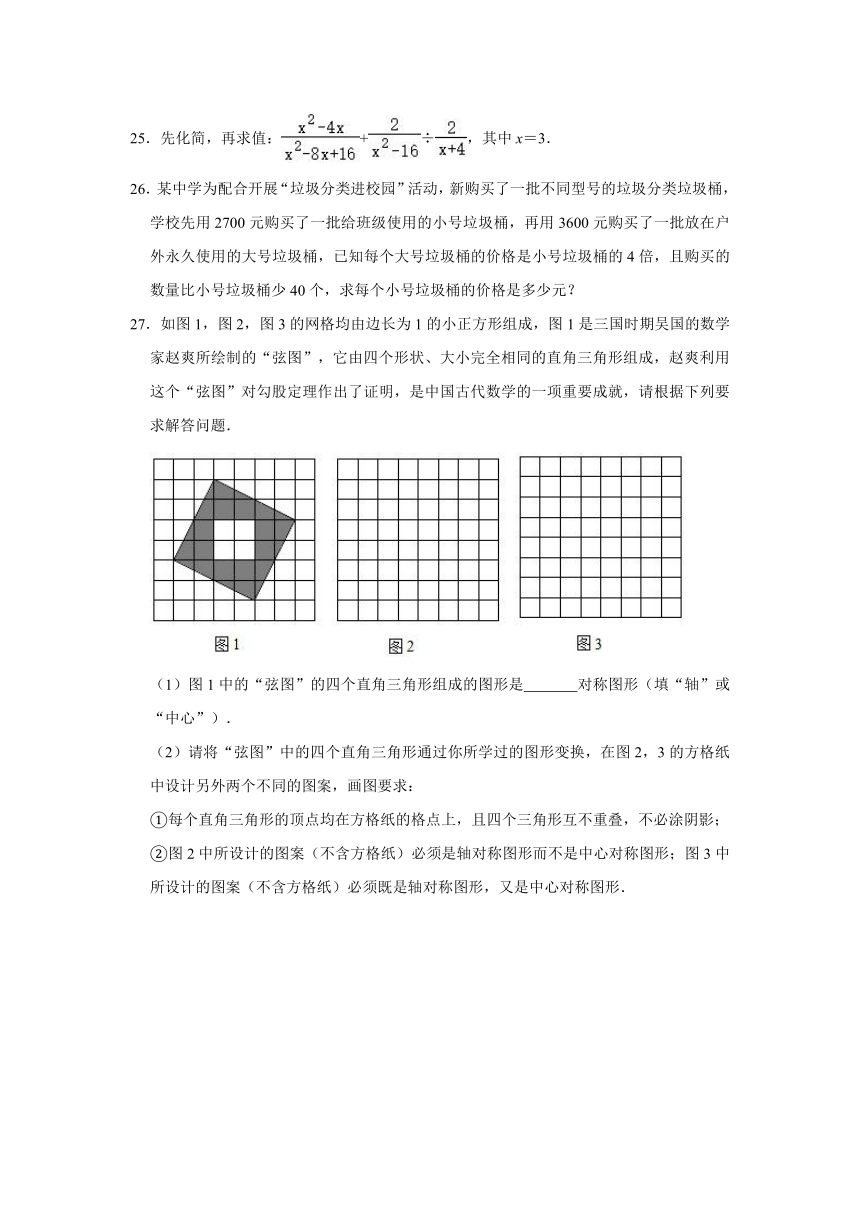
27.如图1,图2,图3的网格均由边长为1的小正方形组成,图1是三国时期吴国的数学家赵爽所绘制的“弦图”,它由四个形状、大小完全相同的直角三角形组成,赵爽利用这个“弦图”对勾股定理作出了证明,是中国古代数学的一项重要成就,请根据下列要求解答问题.
(1)图1中的“弦图”的四个直角三角形组成的图形是 对称图形(填“轴”或“中心”).
(2)请将“弦图”中的四个直角三角形通过你所学过的图形变换,在图2,3的方格纸中设计另外两个不同的图案,画图要求:
①每个直角三角形的顶点均在方格纸的格点上,且四个三角形互不重叠,不必涂阴影;
②图2中所设计的图案(不含方格纸)必须是轴对称图形而不是中心对称图形;图3中所设计的图案(不含方格纸)必须既是轴对称图形,又是中心对称图形.
参考答案
一、单项选择题(共6小题).
1.在下列式子:﹣5x,,a2﹣b2,,中,分式有( )
A.1个 B.2个 C.3个 D.4个
【分析】判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式.
解:,的分母中含有字母,属于分式,其它的属于整式.
故选:B.
2.多项式3x﹣9,x2﹣9与x2﹣6x+9的公因式为( )
A.x+3 B.(x+3)2 C.x﹣3 D.x2+9
【分析】根据公因式定义,对各选项整理然后即可选出有公因式的项.
解:因为3x﹣9=3(x﹣3),x2﹣9=(x+3)(x﹣3),x2﹣6x+9=(x﹣3)2,
所以多项式3x﹣9,x2﹣9与x2﹣6x+9的公因式为(x﹣3).
故选:C.
3.下列运算中,正确的是( )
A.(﹣m)6÷(﹣m)3=﹣m3 B.(﹣a3)2=﹣a6
C.(xy2)2=xy4 D.a2?a3=a6
【分析】分别根据同底数幂的除法法则,幂的乘方与积的乘方运算法则以及同底数幂的乘法法则逐一判断即可.
解:A、(﹣m)6÷(﹣m)3=﹣m3,故本选项符合题意;
B、(﹣a3)2=a6,故本选项不符合题意;
C、(xy2)2=x2y4,故本选项不符合题意;
D、a2?a3=a5,故本选项不符合题意;
故选:A.
4.若a=﹣3﹣2,b=(﹣)﹣2,c=(﹣0.3)0,则a,b,c的大小关系是( )
A.a<b<c B.b<c<a C.c<b<a D.a<c<b
【分析】直接利用负整数指数幂的性质和零指数幂的性质分别化简得出答案.
解:∵a=﹣3﹣2=﹣,b=(﹣)﹣2=9,c=(﹣0.3)0=1,
∴a<c<b.
故选:D.
5.若把x,y的值同时扩大为原来的2倍,则下列分式的值保持不变的是( )
A. B. C. D.
【分析】根据分式的基本性质即可求出答案.
解:A、=2×,分式的值不能保持不变,故此选项不符合题意;
B、=,分式的值保持不变,故此选项符合题意;
C、=,分式的值不能保持不变,故此选项不符合题意;
D、=,分式的值不能保持不变,故此选项不符合题意.
故选:B.
6.下列四个汉字是轴对称图形的是( )
A. B. C. D.
【分析】根据轴对称图形的概念对各选项分析判断即可得解.
解:A、是轴对称图形,故本选项符合题意;
B、不是轴对称图形,故本选项不符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、不是轴对称图形,故本选项不符合题意.
故选:A.
二、填空题(共12小题).
7.单项式﹣6x3y的次数是 4 次.
【分析】直接利用单项式的次数确定方法得出答案.
解:单项式﹣6x3y的次数是4次.
故答案为:4.
8.已知7xay2和﹣9x5yb是同类项,则= .
【分析】根据同类项法则即可求出答案.
解:由题意可知:a=5,b=2,
∴原式=.
故答案为:.
9.当x ≠﹣ 时,分式有意义.
【分析】根据分式有意义的条件可得2x+3≠0,再解即可.
解:由题意得:2x+3≠0,
解得:x≠﹣,
故答案为:≠﹣.
10.在括号内填入适当的整式:(2a+b)( b﹣2a )=b2﹣4a2.
【分析】利用平方差公式的结构特征判断即可.
解:(2a+b)(b﹣2a)=b2﹣4a2.
故答案为:b﹣2a.
11.分解因式:m2+2m﹣3= (m+3)(m﹣1) .
【分析】直接利用十字相乘法分解因式得出答案.
解:m2+2m﹣3=(m+3)(m﹣1).
故答案为:(m+3)(m﹣1).
12.计算:(3a6b3﹣6ab5)÷3ab= a5b2﹣2b4 .
【分析】根据多项式除以单项式的方法,求出算式的值是多少即可.
解:(3a6b3﹣6ab5)÷3ab=a5b2﹣2b4.
故答案为:a5b2﹣2b4.
13.计算:= .
【分析】直接通分运算,再利用分式的加减运算法则计算得出答案.
解:=﹣
=.
故答案为:.
14.一种花的花粉颗粒直径约为0.00065米,0.00065用科学记数法表示为 6.5×10﹣4 .
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数n由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.00065=6.5×10﹣4.
故答案为:6.5×10﹣4.
15.如果关于x的方程有增根,那么k= 1 .
【分析】分式方程去分母转化为整式方程,由分式方程有增根求出x的值,代入整式方程计算即可求出k的值.
解:,
去分母得:1=3(x﹣3)+k,
由分式方程有增根,得到x﹣3=0,即x=3,
把x=3代入整式方程得1=3(3﹣3)+k,
解得k=1.
故答案为:1.
16.若am=6,an=4,则a2m﹣n= 9 .
【分析】根据幂的乘方运算法则以及同底数幂的除法法则计算即可.
解:∵am=6,an=4,
∴a2m﹣n=(am)2÷an=62÷4=36÷4=9.
故答案为:9.
17.在正方形、长方形、线段、等边三角形和平行四边形这五种图形中,是旋转对称图形不是中心对称图形的是 等边三角形 .
【分析】根据中心对称图形的定义以及旋转图形的性质分别判断得出即可.
解:在正方形、长方形、线段、等边三角形和平行四边形这五种图形中正方形、是旋转对称图形不是中心对称图形的是等边三角形.
故答案为:等边三角形.
18.如图,在长方形ABCD中,AB=2cm,BC=3cm,E、F分别是AD、BC的中点,如果将长方形ABFE绕点F顺时针旋转90°,那么旋转后的长方形与长方形CDEF重叠部分的面积是 2.25 cm2.
【分析】将长方形ABFE绕点F顺时针旋转90度,旋转后的长方形与长方形CDEF重叠部分是一个正方形,其边长为FC=1.5cm,根据正方形的面积公式即可求解.
解:如图,将长方形ABFE绕点F顺时针旋转90度,得到长方形A′B′FE′,设A′B′与DC交于点G,
则FC=FB=FB′=BC=1.5cm,
所以旋转后的长方形A′B′FE′与长方形CDEF重叠部分B′FCG是正方形,边长为1.5cm,
所以,面积S=1.5×1.5=2.25(cm2).
故答案是:2.25.
三、解答题(本大题共9小题,第19至21题每题5分,第22至24题每题6分,第25、26题每题7分,第27题5分,共52分)
19.计算:a?a7﹣(﹣3a4)2+a10÷a2.
【分析】分别根据同底数幂的乘除法法则以及积的乘方运算法则化简后,再合并同类项即可.
解:a?a7﹣(﹣3a4)2+a10÷a2
=a8﹣9a8+a8
=﹣7a8.
20.ab(a﹣2+b﹣2).(结果只含有正整数指数幂)
【分析】根据负整数指数幂,可以根据题目的中的要求进行转化,从而可以解答本题.
解:ab(a﹣2+b﹣2)
=ab()
=
=.
21.分解因式:2x3+12x2y+18xy2.
【分析】提公因式2x,再利用完全平方公式进行因式分解即可.
解:2x3+12x2y+18xy2
=2x(x2+6xy+9y2)
=2x(x+3y)2.
22.因式分解:(x2+2x)2﹣7(x2+2x)﹣8.
【分析】原式利用十字相乘法分解后,再利用完全平方公式分解即可.
解:原式=(x2+2x﹣8)(x2+2x+1)=(x﹣2)(x+4)(x+1)2.
23.解分式方程:﹣=1﹣.
【分析】根据解分式方程的过程进行计算即可.
解:去分母得:x﹣1+x+1=x2﹣1﹣x2,
移项,合并同类项得2x=﹣1,
系数化为1得x=﹣,
检验:把x=﹣代入x2﹣1≠0,
所以原方程的解为x=﹣.
24.如图,已知在平面内有三角形ABC和点D,请根据下列要求画出对应的图形,并回答问题.
(1)将△ABC平移,使得点A平移到图中点D的位置,点B、点C的对应点分别为点E、点F,请画出△DEF.
(2)画出△ABC关于点D成中心对称的△A1B1C1.
(3)△DEF与△A1B1C1是否关于某个点成中心对称?如果是,请在图中画出这个对称中心,并记作点O.
【分析】(1)利用点A和点D的位置确定平移方向与距离,然后利用此平移规律画出B、C的对应点E、F即可;
(2)延长AD到A1,使A1D=DA,延长BD到B1,使B1D=DB,延长CD到C1,使C1D=DC;
(3)连接EC1、FB1,EC1、FB1和DA1相交于O点,则可判断△DEF与△A1B1C1关于O点成中心对称.
解:(1)如图,△DEF为所作;
(2)如图,△A1B1C1为所作;
(3)△DEF与△A1B1C1关于点O成中心对称,如图,点O为所作.
25.先化简,再求值:+÷,其中x=3.
【分析】根据分式的除法和加法可以化简题目中的式子,然后将x=3代入化简后的式子即可解答本题.
解:+÷
=
=
=,
当x=3时,原式==﹣4.
26.某中学为配合开展“垃圾分类进校园”活动,新购买了一批不同型号的垃圾分类垃圾桶,学校先用2700元购买了一批给班级使用的小号垃圾桶,再用3600元购买了一批放在户外永久使用的大号垃圾桶,已知每个大号垃圾桶的价格是小号垃圾桶的4倍,且购买的数量比小号垃圾桶少40个,求每个小号垃圾桶的价格是多少元?
【分析】设每个小号垃圾桶的价格是x元,则每个大号垃圾桶的价格是4x元,根据数量=总价÷单价结合用2700元购买的小号垃圾桶比用3600元购买的大号垃圾桶多40个,即可得出关于x的分式方程,解之经检验后即可得出结论.
解:设每个小号垃圾桶的价格是x元,则每个大号垃圾桶的价格是4x元,
依题意,得:﹣=40,
解得:x=45,
经检验,x=45是原方程的解,且符合题意.
答:每个小号垃圾桶的价格是45元.
27.如图1,图2,图3的网格均由边长为1的小正方形组成,图1是三国时期吴国的数学家赵爽所绘制的“弦图”,它由四个形状、大小完全相同的直角三角形组成,赵爽利用这个“弦图”对勾股定理作出了证明,是中国古代数学的一项重要成就,请根据下列要求解答问题.
(1)图1中的“弦图”的四个直角三角形组成的图形是 中心 对称图形(填“轴”或“中心”).
(2)请将“弦图”中的四个直角三角形通过你所学过的图形变换,在图2,3的方格纸中设计另外两个不同的图案,画图要求:
①每个直角三角形的顶点均在方格纸的格点上,且四个三角形互不重叠,不必涂阴影;
②图2中所设计的图案(不含方格纸)必须是轴对称图形而不是中心对称图形;图3中所设计的图案(不含方格纸)必须既是轴对称图形,又是中心对称图形.
【分析】(1)利用中心对称图形的意义得出答案即可;
(2)①每个直角三角形的顶点均在方格纸的格点上,且四个三角形不重叠,是轴对称图形;
②所设计的图案(不含方格纸)必须是中心对称图形或轴对称图形画出图.
解:(1)图1中的“弦图”的四个直角三角形组成的图形是中心对称图形.
故答案为:中心;
(2)如图2是轴对称图形而不是中心对称图形;
图3既是轴对称图形,又是中心对称图形.
一、选择题(共6小题).
1.在下列式子:﹣5x,,a2﹣b2,,中,分式有( )
A.1个 B.2个 C.3个 D.4个
2.多项式3x﹣9,x2﹣9与x2﹣6x+9的公因式为( )
A.x+3 B.(x+3)2 C.x﹣3 D.x2+9
3.下列运算中,正确的是( )
A.(﹣m)6÷(﹣m)3=﹣m3 B.(﹣a3)2=﹣a6
C.(xy2)2=xy4 D.a2?a3=a6
4.若a=﹣3﹣2,b=(﹣)﹣2,c=(﹣0.3)0,则a,b,c的大小关系是( )
A.a<b<c B.b<c<a C.c<b<a D.a<c<b
5.若把x,y的值同时扩大为原来的2倍,则下列分式的值保持不变的是( )
A. B. C. D.
6.下列四个汉字是轴对称图形的是( )
A. B. C. D.
二、填空题(共12小题).
7.单项式﹣6x3y的次数是 次.
8.已知7xay2和﹣9x5yb是同类项,则= .
9.当x 时,分式有意义.
10.在括号内填入适当的整式:(2a+b)( )=b2﹣4a2.
11.分解因式:m2+2m﹣3= .
12.计算:(3a6b3﹣6ab5)÷3ab= .
13.计算:= .
14.一种花的花粉颗粒直径约为0.00065米,0.00065用科学记数法表示为 .
15.如果关于x的方程有增根,那么k= .
16.若am=6,an=4,则a2m﹣n= .
17.在正方形、长方形、线段、等边三角形和平行四边形这五种图形中,是旋转对称图形不是中心对称图形的是 .
18.如图,在长方形ABCD中,AB=2cm,BC=3cm,E、F分别是AD、BC的中点,如果将长方形ABFE绕点F顺时针旋转90°,那么旋转后的长方形与长方形CDEF重叠部分的面积是 cm2.
三、解答题(共9小题).
19.计算:a?a7﹣(﹣3a4)2+a10÷a2.
20.ab(a﹣2+b﹣2).(结果只含有正整数指数幂)
21.分解因式:2x3+12x2y+18xy2.
22.因式分解:(x2+2x)2﹣7(x2+2x)﹣8.
23.解分式方程:﹣=1﹣.
24.如图,已知在平面内有三角形ABC和点D,请根据下列要求画出对应的图形,并回答问题.
(1)将△ABC平移,使得点A平移到图中点D的位置,点B、点C的对应点分别为点E、点F,请画出△DEF.
(2)画出△ABC关于点D成中心对称的△A1B1C1.
(3)△DEF与△A1B1C1是否关于某个点成中心对称?如果是,请在图中画出这个对称中心,并记作点O.
25.先化简,再求值:+÷,其中x=3.
26.某中学为配合开展“垃圾分类进校园”活动,新购买了一批不同型号的垃圾分类垃圾桶,学校先用2700元购买了一批给班级使用的小号垃圾桶,再用3600元购买了一批放在户外永久使用的大号垃圾桶,已知每个大号垃圾桶的价格是小号垃圾桶的4倍,且购买的数量比小号垃圾桶少40个,求每个小号垃圾桶的价格是多少元?
27.如图1,图2,图3的网格均由边长为1的小正方形组成,图1是三国时期吴国的数学家赵爽所绘制的“弦图”,它由四个形状、大小完全相同的直角三角形组成,赵爽利用这个“弦图”对勾股定理作出了证明,是中国古代数学的一项重要成就,请根据下列要求解答问题.
(1)图1中的“弦图”的四个直角三角形组成的图形是 对称图形(填“轴”或“中心”).
(2)请将“弦图”中的四个直角三角形通过你所学过的图形变换,在图2,3的方格纸中设计另外两个不同的图案,画图要求:
①每个直角三角形的顶点均在方格纸的格点上,且四个三角形互不重叠,不必涂阴影;
②图2中所设计的图案(不含方格纸)必须是轴对称图形而不是中心对称图形;图3中所设计的图案(不含方格纸)必须既是轴对称图形,又是中心对称图形.
参考答案
一、单项选择题(共6小题).
1.在下列式子:﹣5x,,a2﹣b2,,中,分式有( )
A.1个 B.2个 C.3个 D.4个
【分析】判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式.
解:,的分母中含有字母,属于分式,其它的属于整式.
故选:B.
2.多项式3x﹣9,x2﹣9与x2﹣6x+9的公因式为( )
A.x+3 B.(x+3)2 C.x﹣3 D.x2+9
【分析】根据公因式定义,对各选项整理然后即可选出有公因式的项.
解:因为3x﹣9=3(x﹣3),x2﹣9=(x+3)(x﹣3),x2﹣6x+9=(x﹣3)2,
所以多项式3x﹣9,x2﹣9与x2﹣6x+9的公因式为(x﹣3).
故选:C.
3.下列运算中,正确的是( )
A.(﹣m)6÷(﹣m)3=﹣m3 B.(﹣a3)2=﹣a6
C.(xy2)2=xy4 D.a2?a3=a6
【分析】分别根据同底数幂的除法法则,幂的乘方与积的乘方运算法则以及同底数幂的乘法法则逐一判断即可.
解:A、(﹣m)6÷(﹣m)3=﹣m3,故本选项符合题意;
B、(﹣a3)2=a6,故本选项不符合题意;
C、(xy2)2=x2y4,故本选项不符合题意;
D、a2?a3=a5,故本选项不符合题意;
故选:A.
4.若a=﹣3﹣2,b=(﹣)﹣2,c=(﹣0.3)0,则a,b,c的大小关系是( )
A.a<b<c B.b<c<a C.c<b<a D.a<c<b
【分析】直接利用负整数指数幂的性质和零指数幂的性质分别化简得出答案.
解:∵a=﹣3﹣2=﹣,b=(﹣)﹣2=9,c=(﹣0.3)0=1,
∴a<c<b.
故选:D.
5.若把x,y的值同时扩大为原来的2倍,则下列分式的值保持不变的是( )
A. B. C. D.
【分析】根据分式的基本性质即可求出答案.
解:A、=2×,分式的值不能保持不变,故此选项不符合题意;
B、=,分式的值保持不变,故此选项符合题意;
C、=,分式的值不能保持不变,故此选项不符合题意;
D、=,分式的值不能保持不变,故此选项不符合题意.
故选:B.
6.下列四个汉字是轴对称图形的是( )
A. B. C. D.
【分析】根据轴对称图形的概念对各选项分析判断即可得解.
解:A、是轴对称图形,故本选项符合题意;
B、不是轴对称图形,故本选项不符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、不是轴对称图形,故本选项不符合题意.
故选:A.
二、填空题(共12小题).
7.单项式﹣6x3y的次数是 4 次.
【分析】直接利用单项式的次数确定方法得出答案.
解:单项式﹣6x3y的次数是4次.
故答案为:4.
8.已知7xay2和﹣9x5yb是同类项,则= .
【分析】根据同类项法则即可求出答案.
解:由题意可知:a=5,b=2,
∴原式=.
故答案为:.
9.当x ≠﹣ 时,分式有意义.
【分析】根据分式有意义的条件可得2x+3≠0,再解即可.
解:由题意得:2x+3≠0,
解得:x≠﹣,
故答案为:≠﹣.
10.在括号内填入适当的整式:(2a+b)( b﹣2a )=b2﹣4a2.
【分析】利用平方差公式的结构特征判断即可.
解:(2a+b)(b﹣2a)=b2﹣4a2.
故答案为:b﹣2a.
11.分解因式:m2+2m﹣3= (m+3)(m﹣1) .
【分析】直接利用十字相乘法分解因式得出答案.
解:m2+2m﹣3=(m+3)(m﹣1).
故答案为:(m+3)(m﹣1).
12.计算:(3a6b3﹣6ab5)÷3ab= a5b2﹣2b4 .
【分析】根据多项式除以单项式的方法,求出算式的值是多少即可.
解:(3a6b3﹣6ab5)÷3ab=a5b2﹣2b4.
故答案为:a5b2﹣2b4.
13.计算:= .
【分析】直接通分运算,再利用分式的加减运算法则计算得出答案.
解:=﹣
=.
故答案为:.
14.一种花的花粉颗粒直径约为0.00065米,0.00065用科学记数法表示为 6.5×10﹣4 .
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数n由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.00065=6.5×10﹣4.
故答案为:6.5×10﹣4.
15.如果关于x的方程有增根,那么k= 1 .
【分析】分式方程去分母转化为整式方程,由分式方程有增根求出x的值,代入整式方程计算即可求出k的值.
解:,
去分母得:1=3(x﹣3)+k,
由分式方程有增根,得到x﹣3=0,即x=3,
把x=3代入整式方程得1=3(3﹣3)+k,
解得k=1.
故答案为:1.
16.若am=6,an=4,则a2m﹣n= 9 .
【分析】根据幂的乘方运算法则以及同底数幂的除法法则计算即可.
解:∵am=6,an=4,
∴a2m﹣n=(am)2÷an=62÷4=36÷4=9.
故答案为:9.
17.在正方形、长方形、线段、等边三角形和平行四边形这五种图形中,是旋转对称图形不是中心对称图形的是 等边三角形 .
【分析】根据中心对称图形的定义以及旋转图形的性质分别判断得出即可.
解:在正方形、长方形、线段、等边三角形和平行四边形这五种图形中正方形、是旋转对称图形不是中心对称图形的是等边三角形.
故答案为:等边三角形.
18.如图,在长方形ABCD中,AB=2cm,BC=3cm,E、F分别是AD、BC的中点,如果将长方形ABFE绕点F顺时针旋转90°,那么旋转后的长方形与长方形CDEF重叠部分的面积是 2.25 cm2.
【分析】将长方形ABFE绕点F顺时针旋转90度,旋转后的长方形与长方形CDEF重叠部分是一个正方形,其边长为FC=1.5cm,根据正方形的面积公式即可求解.
解:如图,将长方形ABFE绕点F顺时针旋转90度,得到长方形A′B′FE′,设A′B′与DC交于点G,
则FC=FB=FB′=BC=1.5cm,
所以旋转后的长方形A′B′FE′与长方形CDEF重叠部分B′FCG是正方形,边长为1.5cm,
所以,面积S=1.5×1.5=2.25(cm2).
故答案是:2.25.
三、解答题(本大题共9小题,第19至21题每题5分,第22至24题每题6分,第25、26题每题7分,第27题5分,共52分)
19.计算:a?a7﹣(﹣3a4)2+a10÷a2.
【分析】分别根据同底数幂的乘除法法则以及积的乘方运算法则化简后,再合并同类项即可.
解:a?a7﹣(﹣3a4)2+a10÷a2
=a8﹣9a8+a8
=﹣7a8.
20.ab(a﹣2+b﹣2).(结果只含有正整数指数幂)
【分析】根据负整数指数幂,可以根据题目的中的要求进行转化,从而可以解答本题.
解:ab(a﹣2+b﹣2)
=ab()
=
=.
21.分解因式:2x3+12x2y+18xy2.
【分析】提公因式2x,再利用完全平方公式进行因式分解即可.
解:2x3+12x2y+18xy2
=2x(x2+6xy+9y2)
=2x(x+3y)2.
22.因式分解:(x2+2x)2﹣7(x2+2x)﹣8.
【分析】原式利用十字相乘法分解后,再利用完全平方公式分解即可.
解:原式=(x2+2x﹣8)(x2+2x+1)=(x﹣2)(x+4)(x+1)2.
23.解分式方程:﹣=1﹣.
【分析】根据解分式方程的过程进行计算即可.
解:去分母得:x﹣1+x+1=x2﹣1﹣x2,
移项,合并同类项得2x=﹣1,
系数化为1得x=﹣,
检验:把x=﹣代入x2﹣1≠0,
所以原方程的解为x=﹣.
24.如图,已知在平面内有三角形ABC和点D,请根据下列要求画出对应的图形,并回答问题.
(1)将△ABC平移,使得点A平移到图中点D的位置,点B、点C的对应点分别为点E、点F,请画出△DEF.
(2)画出△ABC关于点D成中心对称的△A1B1C1.
(3)△DEF与△A1B1C1是否关于某个点成中心对称?如果是,请在图中画出这个对称中心,并记作点O.
【分析】(1)利用点A和点D的位置确定平移方向与距离,然后利用此平移规律画出B、C的对应点E、F即可;
(2)延长AD到A1,使A1D=DA,延长BD到B1,使B1D=DB,延长CD到C1,使C1D=DC;
(3)连接EC1、FB1,EC1、FB1和DA1相交于O点,则可判断△DEF与△A1B1C1关于O点成中心对称.
解:(1)如图,△DEF为所作;
(2)如图,△A1B1C1为所作;
(3)△DEF与△A1B1C1关于点O成中心对称,如图,点O为所作.
25.先化简,再求值:+÷,其中x=3.
【分析】根据分式的除法和加法可以化简题目中的式子,然后将x=3代入化简后的式子即可解答本题.
解:+÷
=
=
=,
当x=3时,原式==﹣4.
26.某中学为配合开展“垃圾分类进校园”活动,新购买了一批不同型号的垃圾分类垃圾桶,学校先用2700元购买了一批给班级使用的小号垃圾桶,再用3600元购买了一批放在户外永久使用的大号垃圾桶,已知每个大号垃圾桶的价格是小号垃圾桶的4倍,且购买的数量比小号垃圾桶少40个,求每个小号垃圾桶的价格是多少元?
【分析】设每个小号垃圾桶的价格是x元,则每个大号垃圾桶的价格是4x元,根据数量=总价÷单价结合用2700元购买的小号垃圾桶比用3600元购买的大号垃圾桶多40个,即可得出关于x的分式方程,解之经检验后即可得出结论.
解:设每个小号垃圾桶的价格是x元,则每个大号垃圾桶的价格是4x元,
依题意,得:﹣=40,
解得:x=45,
经检验,x=45是原方程的解,且符合题意.
答:每个小号垃圾桶的价格是45元.
27.如图1,图2,图3的网格均由边长为1的小正方形组成,图1是三国时期吴国的数学家赵爽所绘制的“弦图”,它由四个形状、大小完全相同的直角三角形组成,赵爽利用这个“弦图”对勾股定理作出了证明,是中国古代数学的一项重要成就,请根据下列要求解答问题.
(1)图1中的“弦图”的四个直角三角形组成的图形是 中心 对称图形(填“轴”或“中心”).
(2)请将“弦图”中的四个直角三角形通过你所学过的图形变换,在图2,3的方格纸中设计另外两个不同的图案,画图要求:
①每个直角三角形的顶点均在方格纸的格点上,且四个三角形互不重叠,不必涂阴影;
②图2中所设计的图案(不含方格纸)必须是轴对称图形而不是中心对称图形;图3中所设计的图案(不含方格纸)必须既是轴对称图形,又是中心对称图形.
【分析】(1)利用中心对称图形的意义得出答案即可;
(2)①每个直角三角形的顶点均在方格纸的格点上,且四个三角形不重叠,是轴对称图形;
②所设计的图案(不含方格纸)必须是中心对称图形或轴对称图形画出图.
解:(1)图1中的“弦图”的四个直角三角形组成的图形是中心对称图形.
故答案为:中心;
(2)如图2是轴对称图形而不是中心对称图形;
图3既是轴对称图形,又是中心对称图形.
同课章节目录
