山东省菏泽市成武县2020-2021学年八年级上学期期末学业质量测评数学试题(含答案)
文档属性
| 名称 | 山东省菏泽市成武县2020-2021学年八年级上学期期末学业质量测评数学试题(含答案) | 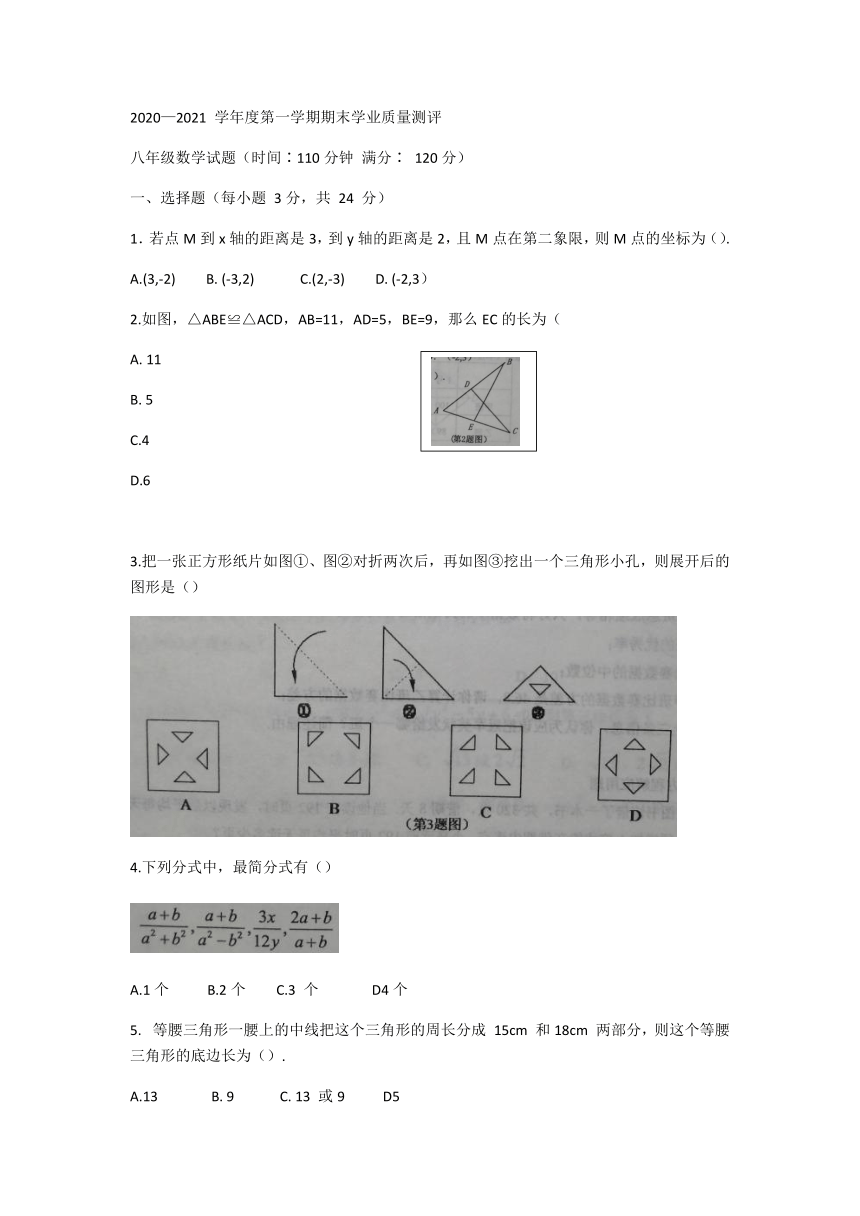 | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-03 19:04:15 | ||
图片预览



文档简介
12192000122936002020—2021 学年度第一学期期末学业质量测评
八年级数学试题(时间∶110分钟 满分∶ 120分)
一、选择题(每小题 3分,共 24 分)
1.若点M到x轴的距离是3,到y轴的距离是2,且M点在第二象限,则M点的坐标为().
A.(3,-2) B. (-3,2) C.(2,-3) D. (-2,3)
2.如图,△ABE≌△ACD,AB=11,AD=5,BE=9,那么EC的长为(
255778047625
A. 11
B. 5
C.4
D.6
3.把一张正方形纸片如图①、图②对折两次后,再如图③挖出一个三角形小孔,则展开后的图形是()
4.下列分式中,最简分式有()
A.1个 B.2个 C.3 个 D4个
等腰三角形一腰上的中线把这个三角形的周长分成 15cm 和18cm 两部分,则这个等腰三角形的底边长为().
A.13 B. 9 C. 13 或9 D5
6. 某公司有 15名工作人员,他们的月工资情况如下表所示∶
则该公司工作人员月工资的中位数、众数分别为( )
A.2800,2000 B.2000,2000 C. 5000,8000 D. 2800,8000
7.下列命题中,真命题是()
A. 两条直线被第三条直线所截,同位角相等.
B.相等的角是对顶角.
C. 三角形的外角和等于 360°
D.三角形的外角大于它的任一内角.
8.在学校的一次卫生检查中,八年级一班的教室卫生成绩评为85分,环境卫生成绩评为90分,个人卫生成绩评为 90分.如果三项成绩分别按 40%,40%。和 20%计入总成绩,则该班这次卫生检查的总成绩是()
A.85 B. 88 C.90 D.95
二、填空题(每小题 3分,共 18 分)
9.已知点A(m-1,2),点B(3,2m),且AB//y轴,则点B的坐标为
10.如图,将一张长方形纸片 ABCD 沿它的一条对角线 BD 折叠后,点C落在点F处,BF交AD于E,若∠FDB=66°,则∠BED的度数是
11.的最简公分母是
12.一组数据2,4,5,1,a的平均数为a,则这组数据的方差是__
13."线段垂直平分线上的点到线段两端的距离相等."的逆命题是
14.分式的值为0,则x的值是__
三、解答题(本题满分78 分,要写出必要的计算、推理、解答过程)
(8分)如图,在△ABC中,AB=AC,AD是BC边上的中线,延长 CB至点E,延长BC至点F,使BE=CF,连结 AE,AF.求证∶ AD 平分∠EAF.
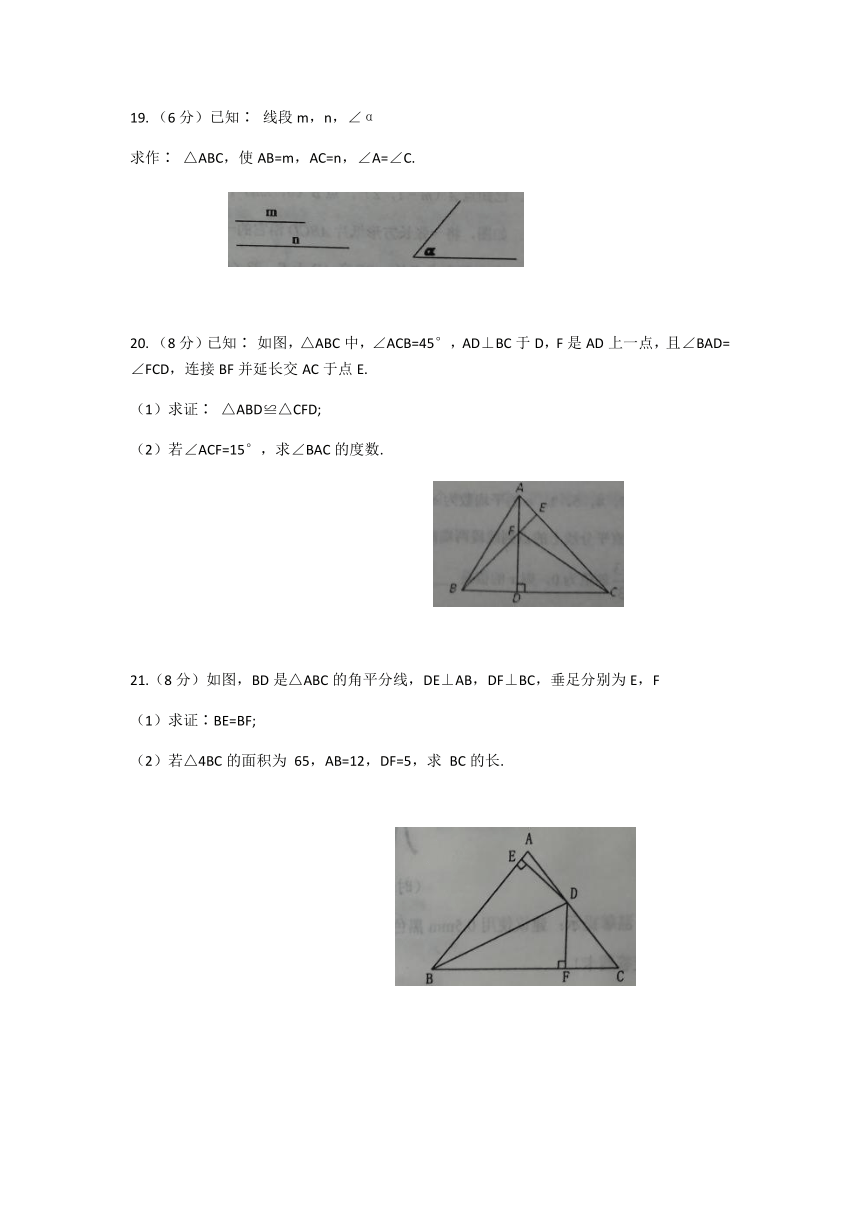
(6分)已知∶ 线段m,n,∠α
求作∶ △ABC,使AB=m,AC=n,∠A=∠C.
(8分)已知∶ 如图,△ABC中,∠ACB=45°,AD⊥BC于D,F是AD上一点,且∠BAD=∠FCD,连接BF并延长交AC于点E.
(1)求证∶ △ABD≌△CFD;
(2)若∠ACF=15°,求∠BAC的度数.
21.(8分)如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC,垂足分别为E,F
(1)求证∶BE=BF;
(2)若△4BC的面积为 65,AB=12,DF=5,求 BC的长.
22.(8分)某校九年级学生开展踢键子比赛活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢 100 个以上(含 100 个)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位∶个)
经统计发现两班总成绩相等,只好将数据中的其他信息作为参考.根据要求回答下列问题∶
计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)经计算甲班比赛数据的方差是 46.8,请你计算乙班比赛数据的方差;
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班?简述理由.
23.(10分)列方程解应用题
小亮从图书馆借了一本书,共 320 页,借期8天.当他读完 192 页时,发现以后平均每天读书的页数必须增加1倍才能在借期内读完.小亮读前 192 页时平均每天读多少页?
八年级数学试题(时间∶110分钟 满分∶ 120分)
一、选择题(每小题 3分,共 24 分)
1.若点M到x轴的距离是3,到y轴的距离是2,且M点在第二象限,则M点的坐标为().
A.(3,-2) B. (-3,2) C.(2,-3) D. (-2,3)
2.如图,△ABE≌△ACD,AB=11,AD=5,BE=9,那么EC的长为(
255778047625
A. 11
B. 5
C.4
D.6
3.把一张正方形纸片如图①、图②对折两次后,再如图③挖出一个三角形小孔,则展开后的图形是()
4.下列分式中,最简分式有()
A.1个 B.2个 C.3 个 D4个
等腰三角形一腰上的中线把这个三角形的周长分成 15cm 和18cm 两部分,则这个等腰三角形的底边长为().
A.13 B. 9 C. 13 或9 D5
6. 某公司有 15名工作人员,他们的月工资情况如下表所示∶
则该公司工作人员月工资的中位数、众数分别为( )
A.2800,2000 B.2000,2000 C. 5000,8000 D. 2800,8000
7.下列命题中,真命题是()
A. 两条直线被第三条直线所截,同位角相等.
B.相等的角是对顶角.
C. 三角形的外角和等于 360°
D.三角形的外角大于它的任一内角.
8.在学校的一次卫生检查中,八年级一班的教室卫生成绩评为85分,环境卫生成绩评为90分,个人卫生成绩评为 90分.如果三项成绩分别按 40%,40%。和 20%计入总成绩,则该班这次卫生检查的总成绩是()
A.85 B. 88 C.90 D.95
二、填空题(每小题 3分,共 18 分)
9.已知点A(m-1,2),点B(3,2m),且AB//y轴,则点B的坐标为
10.如图,将一张长方形纸片 ABCD 沿它的一条对角线 BD 折叠后,点C落在点F处,BF交AD于E,若∠FDB=66°,则∠BED的度数是
11.的最简公分母是
12.一组数据2,4,5,1,a的平均数为a,则这组数据的方差是__
13."线段垂直平分线上的点到线段两端的距离相等."的逆命题是
14.分式的值为0,则x的值是__
三、解答题(本题满分78 分,要写出必要的计算、推理、解答过程)
(8分)如图,在△ABC中,AB=AC,AD是BC边上的中线,延长 CB至点E,延长BC至点F,使BE=CF,连结 AE,AF.求证∶ AD 平分∠EAF.
(6分)已知∶ 线段m,n,∠α
求作∶ △ABC,使AB=m,AC=n,∠A=∠C.
(8分)已知∶ 如图,△ABC中,∠ACB=45°,AD⊥BC于D,F是AD上一点,且∠BAD=∠FCD,连接BF并延长交AC于点E.
(1)求证∶ △ABD≌△CFD;
(2)若∠ACF=15°,求∠BAC的度数.
21.(8分)如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC,垂足分别为E,F
(1)求证∶BE=BF;
(2)若△4BC的面积为 65,AB=12,DF=5,求 BC的长.
22.(8分)某校九年级学生开展踢键子比赛活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢 100 个以上(含 100 个)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位∶个)
经统计发现两班总成绩相等,只好将数据中的其他信息作为参考.根据要求回答下列问题∶
计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)经计算甲班比赛数据的方差是 46.8,请你计算乙班比赛数据的方差;
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班?简述理由.
23.(10分)列方程解应用题
小亮从图书馆借了一本书,共 320 页,借期8天.当他读完 192 页时,发现以后平均每天读书的页数必须增加1倍才能在借期内读完.小亮读前 192 页时平均每天读多少页?
同课章节目录
