5.3.1 平行线的性质 课件(共18张PPT)
文档属性
| 名称 | 5.3.1 平行线的性质 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-07 18:24:49 | ||
图片预览





文档简介
5.3.1 平行线的性质
第五章 相交线与平行线
2021年春人教版七年级数学下册
1、理解平行线的性质。
2、能初步运用平行线的性质进行有关计算。
3、体会“观察-猜想-证明”的探索方法,培养学生辩证和逻辑能力。
平行线性质的研究和探索。(重点)
正确区分平行线的性质和判定。( 难点)
学习目标
平行线判定方法1:
平行线判定方法2:
平行线判定方法3:
同位角相等,两直线平行。
内错角相等,两直线平行。
同旁内角互补,两直线平行。
上节课通过同位角、内错角、同旁内角
之间的关系证明平行线的过程,
这节课我们学习已知两直线平行,
同位角、内错角、同旁内角存在什么关系?
知识回顾
任意画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角。 选几组同位角,度量这些角,把结果填入下表:
a
b
c
1
3
2
4
8
5
7
6
角
∠1
∠2
∠3
∠4
度数
角
∠5
∠6
∠7
∠8
度数
问题一:找出图中的角中,哪些是同位角?
问题二:观察度量结果,你发现了它们之间的度数有什么关系?
问题三:猜想两条平行线被第三条直线所截得的同位角有什么关系吗?
探究新知
任意画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角。 选几组同位角,度量这些角,把结果填入下表:
角
∠1
∠2
∠3
∠4
度数
角
∠5
∠6
∠7
∠8
度数
a
b
c
1
3
2
4
8
5
7
6
问题四:任意画一条截线d,同样度量并比较各对同位角的度数,猜想还成立吗?
d
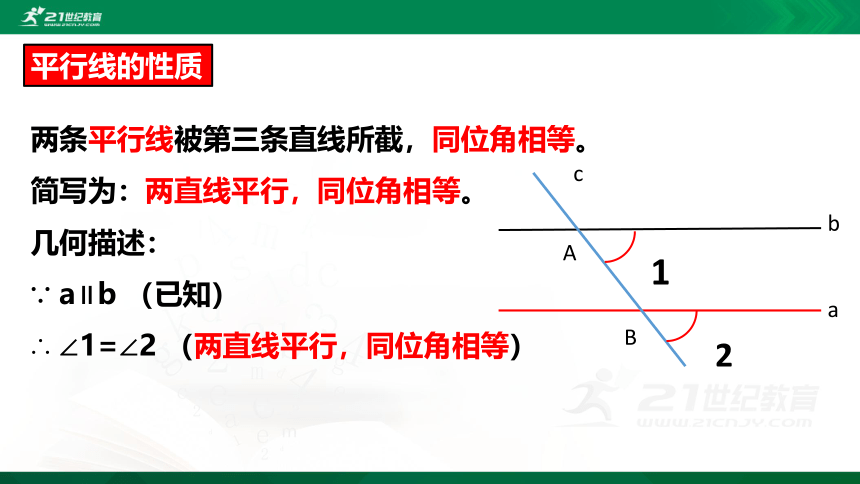
平行线的性质
两条平行线被第三条直线所截,同位角相等。
简写为:两直线平行,同位角相等。
几何描述:
∵ a∥b (已知)
∴ ∠1=∠2 (两直线平行,同位角相等)
a
b
c
1
2
A
B
a
b
c
1
2
A
B
3
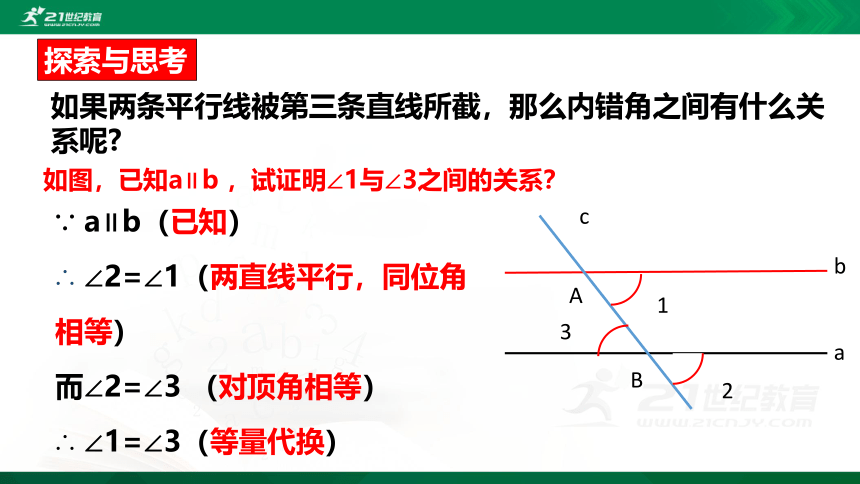
如果两条平行线被第三条直线所截,那么内错角之间有什么关系呢?
∵ a∥b(已知)
∴ ∠2=∠1(两直线平行,同位角相等)
而∠2=∠3 (对顶角相等)
∴ ∠1=∠3(等量代换)
如图,已知a∥b ,试证明∠1与∠3之间的关系?
探索与思考
两条平行线被第三条直线所截,内错角相等。
简写为:两直线平行,内错角相等。
几何描述:
∵ a∥b (已知)
∴ ∠1=∠2 (两直线平行,内错角相等)
a
b
c
1
A
B
2
探索与思考
a
b
c
1
2
A
B
3
如果两条平行线被第三条直线所截,那么同旁内角之间有什么关系呢?
∵ a∥b (已知)
∴ ∠2=∠1(两直线平行,同位角相等)
而∠2+∠3 =180°
∴ ∠1+∠3 =180°(等量代换)
如图,已知a∥b ,探究∠1与∠3之间的关系?
探索与思考
两条平行线被第三条直线所截,同旁内角互补。
简写为:两直线平行,同旁内角互补。
几何描述:
∵ a∥b (已知)
∴ ∠1+∠3 = 180° (两直线平行,同旁内角互补)
a
b
c
1
2
A
B
3
平行线的性质
1,如下图一块梯形贴片的残余部分,已知∠A=105°,∠B=112°,另外两个角分别是多少度?
A
B
C
D
解:∵该四边形ABCD是梯形
∴AB∥CD
∴∠A+∠D=180°
∠B+∠C=180°(两直线平行,同旁内角互补)
∴ ∠D=180°- ∠A = 180°- 105°=75°
∠C=180°- ∠B = 180°- 112°=68°
所以梯形的另外两个角分别是75°、68°
课堂练习
如图,直线????,????被????,????所截,且????//????,则下列结论中正确的是( )
A.∠1=∠2 B.∠3=∠4
C.∠2+∠4=180? D.∠1+∠4=180?
?
【答案】B
【详解】如图,∵a//b,
∴∠1=∠5,∠3=∠4,
∵∠2+∠5=180°,∴无法得到∠2=∠5,即得不到∠1=∠2,
由已知得不到∠2+∠4=180? 、∠1+∠4=180?,
故选B.
?
2,
3,如图,直线a∥b,直线AB⊥AC,若∠1=47°,则∠2的度数为()
A.50° B.45° C.30° D.43°
【答案】D
【详解】
解:∵直线a∥b,
∴∠ABC=∠2,
∵AB⊥AC ,
∴∠1+∠ABC=90° 而∠1=47° .
∴∠2=43°.
故选:D.
4,如图,已知CD∥BE,?如果∠1=55°,?那么∠B的度数为( )
A.70° B.100° C.110° D.125°
【答案】D
【详解】
解:∵∠1=55°,
∴∠2=180°- 60°=125°.
∵CD∥BE,
∴∠2=∠B=125°.
故选:D.
5,如图所示,直线a∥b,∠1=35°,∠2=90°则∠3的度数为( )
A.125° B.135° C.145° D.155°
【答案】A
【解析】
∵a∥b,∴∠1=∠4=35°,
∵∠2=90°,∴∠4+∠5=90°,
∴∠5=55°,∴∠3=180°-∠5=125°,
故选:A.
6,变式 如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )
A.132° B.134° C.136° D.138°
【答案】B
【解析】
解:过E作EF∥AB,
∵AB∥CD,∴AB∥CD∥EF,
∴∠C=∠FEC,∠BAE=∠FEA,
∵∠C=44°,∠AEC为直角,
∴∠FEC=44°,∠BAE=∠AEF=90°﹣44°=46°,
∴∠1=180°﹣∠BAE=180°﹣46°=134°,故选B.
谢谢聆听
第五章 相交线与平行线
2021年春人教版七年级数学下册
1、理解平行线的性质。
2、能初步运用平行线的性质进行有关计算。
3、体会“观察-猜想-证明”的探索方法,培养学生辩证和逻辑能力。
平行线性质的研究和探索。(重点)
正确区分平行线的性质和判定。( 难点)
学习目标
平行线判定方法1:
平行线判定方法2:
平行线判定方法3:
同位角相等,两直线平行。
内错角相等,两直线平行。
同旁内角互补,两直线平行。
上节课通过同位角、内错角、同旁内角
之间的关系证明平行线的过程,
这节课我们学习已知两直线平行,
同位角、内错角、同旁内角存在什么关系?
知识回顾
任意画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角。 选几组同位角,度量这些角,把结果填入下表:
a
b
c
1
3
2
4
8
5
7
6
角
∠1
∠2
∠3
∠4
度数
角
∠5
∠6
∠7
∠8
度数
问题一:找出图中的角中,哪些是同位角?
问题二:观察度量结果,你发现了它们之间的度数有什么关系?
问题三:猜想两条平行线被第三条直线所截得的同位角有什么关系吗?
探究新知
任意画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角。 选几组同位角,度量这些角,把结果填入下表:
角
∠1
∠2
∠3
∠4
度数
角
∠5
∠6
∠7
∠8
度数
a
b
c
1
3
2
4
8
5
7
6
问题四:任意画一条截线d,同样度量并比较各对同位角的度数,猜想还成立吗?
d
平行线的性质
两条平行线被第三条直线所截,同位角相等。
简写为:两直线平行,同位角相等。
几何描述:
∵ a∥b (已知)
∴ ∠1=∠2 (两直线平行,同位角相等)
a
b
c
1
2
A
B
a
b
c
1
2
A
B
3
如果两条平行线被第三条直线所截,那么内错角之间有什么关系呢?
∵ a∥b(已知)
∴ ∠2=∠1(两直线平行,同位角相等)
而∠2=∠3 (对顶角相等)
∴ ∠1=∠3(等量代换)
如图,已知a∥b ,试证明∠1与∠3之间的关系?
探索与思考
两条平行线被第三条直线所截,内错角相等。
简写为:两直线平行,内错角相等。
几何描述:
∵ a∥b (已知)
∴ ∠1=∠2 (两直线平行,内错角相等)
a
b
c
1
A
B
2
探索与思考
a
b
c
1
2
A
B
3
如果两条平行线被第三条直线所截,那么同旁内角之间有什么关系呢?
∵ a∥b (已知)
∴ ∠2=∠1(两直线平行,同位角相等)
而∠2+∠3 =180°
∴ ∠1+∠3 =180°(等量代换)
如图,已知a∥b ,探究∠1与∠3之间的关系?
探索与思考
两条平行线被第三条直线所截,同旁内角互补。
简写为:两直线平行,同旁内角互补。
几何描述:
∵ a∥b (已知)
∴ ∠1+∠3 = 180° (两直线平行,同旁内角互补)
a
b
c
1
2
A
B
3
平行线的性质
1,如下图一块梯形贴片的残余部分,已知∠A=105°,∠B=112°,另外两个角分别是多少度?
A
B
C
D
解:∵该四边形ABCD是梯形
∴AB∥CD
∴∠A+∠D=180°
∠B+∠C=180°(两直线平行,同旁内角互补)
∴ ∠D=180°- ∠A = 180°- 105°=75°
∠C=180°- ∠B = 180°- 112°=68°
所以梯形的另外两个角分别是75°、68°
课堂练习
如图,直线????,????被????,????所截,且????//????,则下列结论中正确的是( )
A.∠1=∠2 B.∠3=∠4
C.∠2+∠4=180? D.∠1+∠4=180?
?
【答案】B
【详解】如图,∵a//b,
∴∠1=∠5,∠3=∠4,
∵∠2+∠5=180°,∴无法得到∠2=∠5,即得不到∠1=∠2,
由已知得不到∠2+∠4=180? 、∠1+∠4=180?,
故选B.
?
2,
3,如图,直线a∥b,直线AB⊥AC,若∠1=47°,则∠2的度数为()
A.50° B.45° C.30° D.43°
【答案】D
【详解】
解:∵直线a∥b,
∴∠ABC=∠2,
∵AB⊥AC ,
∴∠1+∠ABC=90° 而∠1=47° .
∴∠2=43°.
故选:D.
4,如图,已知CD∥BE,?如果∠1=55°,?那么∠B的度数为( )
A.70° B.100° C.110° D.125°
【答案】D
【详解】
解:∵∠1=55°,
∴∠2=180°- 60°=125°.
∵CD∥BE,
∴∠2=∠B=125°.
故选:D.
5,如图所示,直线a∥b,∠1=35°,∠2=90°则∠3的度数为( )
A.125° B.135° C.145° D.155°
【答案】A
【解析】
∵a∥b,∴∠1=∠4=35°,
∵∠2=90°,∴∠4+∠5=90°,
∴∠5=55°,∴∠3=180°-∠5=125°,
故选:A.
6,变式 如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )
A.132° B.134° C.136° D.138°
【答案】B
【解析】
解:过E作EF∥AB,
∵AB∥CD,∴AB∥CD∥EF,
∴∠C=∠FEC,∠BAE=∠FEA,
∵∠C=44°,∠AEC为直角,
∴∠FEC=44°,∠BAE=∠AEF=90°﹣44°=46°,
∴∠1=180°﹣∠BAE=180°﹣46°=134°,故选B.
谢谢聆听
