5.4 角的比较 课件（共25张PPT）

第五章 基本平面图形
4 角的比较
知识点一 角的大小比较
内容
角度
举例
度量法


叠合法


重要提示
知识点一 角的大小比较
内容
角度
举例
度量法
（1）对“中”——角的顶点对准量角器的中心；
（2）重合——角的一边与量角器的零刻度线重合；
（3）读数——读出角的另一边所对的度数；
（4）比较度数
数
因为∠AOB＝70°，∠A′O′B′＝40°，所以∠AOB＞∠A′O′B′
叠合法
（1）将两个角的顶点及一边重合；
（2）使两个角的另一边落在重合一边的同侧；
（3）由两个角的另一边的位置确定两个角的大小
形
∠AOB＞∠A′O′B′
重要提示
两个角的比较还可用中间值法，通过两个角与中间值的比较，得出大小关系
例1
如图为两块直角三角板.
（1）用叠合法比较∠1，∠a的大小；
（2）量出图中各角的度数，并把图中的6个角从小到大排列，然后用“＜”或“＝”连接.
解析
（1）如下图所示，把两块三角板叠放在一起，可得∠l＞∠a.





（2）用量角器量出题图中各个角的度数，分别是∠1＝∠2＝45°，∠3＝90°，∠a＝30°，∠β＝60°，∠γ＝90°，把它们从小到大排列，得∠a＜∠1＝∠2＜∠β＜∠3＝∠γ.
知识点二 角的平分线及相关计算
定义
举例

性质和判定
角平分线的基本性质
角平分线的基本判定方法
重要
提示
知识点二 角的平分线及相关计算
定义
从一个角的顶点出发，把这个角分成相等的两个角的射线，叫做这个角的平分线
举例
如图，射线OC把∠AOB分成两个相等的角，射线OC叫做∠AOB的平分线
性质和判定
角平分线的基本性质
角平分线的基本判定方法
因为OC是∠AOB的平分线，所以∠AOB＝2∠1＝2∠2，∠1＝∠2＝ ∠AOB
①因为∠AOB＝2∠1，所以OC是∠AOB的平分线；②因为∠1＝∠2，所以OC是∠AOB的平分线；③因为∠2＝ ∠AOB，所以OC是∠AOB的平分线
重要
提示
角的平分线是一条在角的内部的射线，不是线段，也不是直线
例2
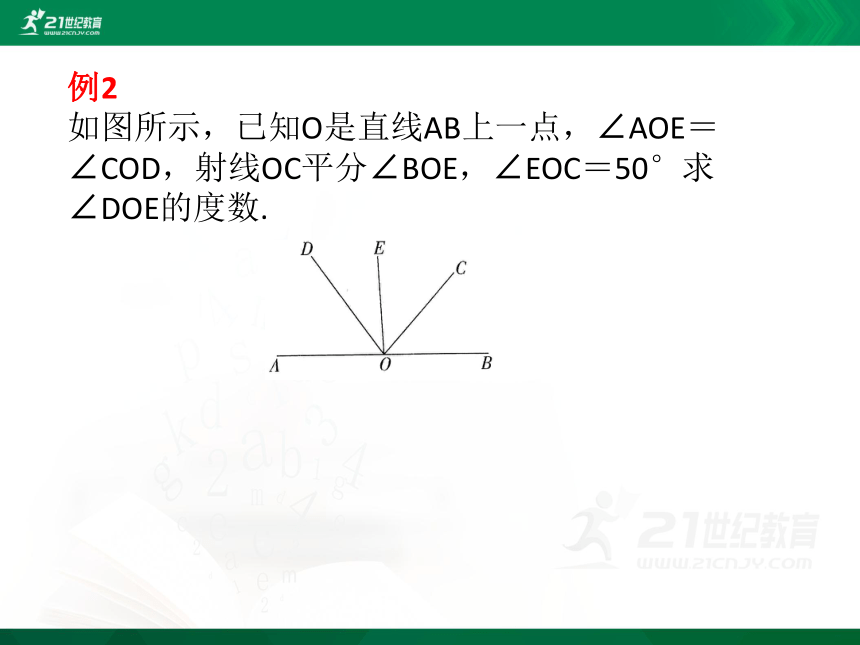
如图所示，已知O是直线AB上一点，∠AOE＝∠COD，射线OC平分∠BOE，∠EOC＝50°求∠DOE的度数.
分析
由∠AOE＝∠COD，得∠AOD＝∠EOC＝50°，由射线OC平分∠BOE，得∠BOC＝∠EOC＝50°，由平角减去∠AOD、∠EOC和∠BOC，可得∠DOE的度数.
分析
由∠AOE＝∠COD，得∠AOD＝∠EOC＝50°，由射线OC平分∠BOE，得∠BOC＝∠EOC＝50°，由平角减去∠AOD、∠EOC和∠BOC，可得∠DOE的度数.
解析
因为∠AOE＝∠COD，所以∠AOE-∠DOE＝∠COD-∠DOE，即∠AOD＝∠EOC＝50°，因为射线OC平分∠BOE，所以∠COB＝∠EOC＝50°，所以∠DOE＝180°-3×50°＝30°.
分析
由∠AOE＝∠COD，得∠AOD＝∠EOC＝50°，由射线OC平分∠BOE，得∠BOC＝∠EOC＝50°，由平角减去∠AOD、∠EOC和∠BOC，可得∠DOE的度数.
解析
因为∠AOE＝∠COD，所以∠AOE-∠DOE＝∠COD-∠DOE，即∠AOD＝∠EOC＝50°，因为射线OC平分∠BOE，所以∠COB＝∠EOC＝50°，所以∠DOE＝180°-3×50°＝30°.
提示
平角等于180°是题目中的隐含条件，要注意挖掘.
经典例题
题型一 一副三角板中角的计算
例1
下图是一副三角板拼成的图案，其中∠ACB＝∠EBD＝90°若∠EBC＝4∠ABD，则∠ABD的度数为______.



解析
因为∠EBD＝90°，∠ABC＝60°，所以∠EBC＋∠ABD＝∠EBD＋∠ABC＝90°＋60°＝150°，因为∠EBC＝4∠ABD，所以4∠ABD＋∠ABD＝150°所以∠ABD＝30°.
答案 30°
解析
因为∠EBD＝90°，∠ABC＝60°，所以∠EBC＋∠ABD＝∠EBD＋∠ABC＝90°＋60°＝150°，因为∠EBC＝4∠ABD，所以4∠ABD＋∠ABD＝150°所以∠ABD＝30°.
答案 30°
规律总结
共顶点的两个角形成的角中，最大的钝角与叠合部分的角相加等于共顶点的两个角的和.
题型二 借助一元一次方程求角的度数
例2
如下图，OC平分∠AOB，∠AOD:∠BOD＝3:5，已知∠COD＝15°，求∠AOB的度数.



解析
因为∠AOD:∠BOD＝3:5，所以设∠AOD＝3x，则∠BOD＝5x.所以∠AOB＝∠AOD＋∠BOD＝3x＋5x＝8x.因为OC平分∠AOB，所以∠AOC＝ ∠AOB＝
×8x＝4x.所以∠COD＝∠AOC-∠AOD＝4x-3x＝x.因为∠COD＝15°，所以x＝15°所以∠AOB＝8x＝8×15°＝120°.
解析
因为∠AOD:∠BOD＝3:5，所以设∠AOD＝3x，则∠BOD＝5x.所以∠AOB＝∠AOD＋∠BOD＝3x＋5x＝8x.因为OC平分∠AOB，所以∠AOC＝ ∠AOB＝
×8x＝4x.所以∠COD＝∠AOC-∠AOD＝4x-3x＝x.因为∠COD＝15°，所以x＝15°所以∠AOB＝8x＝8×15°＝120°.
温馨提示
当所给的角以比的形式出现时，常常设出份数，建立方程求解.
题型三 运用整体思想求角的度数
例3
如图所示，OC是∠AOD的平分线，OE是∠DOB的平分线.
（1）如果∠AOB＝130°，那么∠COE是多少度？
（2）如果∠COE＝a，那么∠AOB是多少度？
解析
因为OC是∠AOD的平分线，所以∠COD＝ ∠AOD.
因为OE是∠BOD的平分线，所以∠DOE＝ ∠BOD.
所以∠COD＋∠DOE＝ ∠AOD＋ ∠BOD＝ （∠AOD＋∠BOD）.
因为∠COD＋∠DOE＝∠COE，∠AOD＋∠BOD＝∠AOB，
所以∠COE＝ ∠AOB.
（1）因为∠AOB＝130°，所以∠COE＝65°.
（2）因为∠COE＝a，所以∠AOB＝2∠COE＝2a.
解析
因为OC是∠AOD的平分线，所以∠COD＝ ∠AOD.
因为OE是∠BOD的平分线，所以∠DOE＝ ∠BOD.
所以∠COD＋∠DOE＝ ∠AOD＋ ∠BOD＝ （∠AOD＋∠BOD）.
因为∠COD＋∠DOE＝∠COE，∠AOD＋∠BOD＝∠AOB，
所以∠COE＝ ∠AOB.
（1）因为∠AOB＝130°，所以∠COE＝65°.
（2）因为∠COE＝a，所以∠AOB＝2∠COE＝2a.
点拨
本题运用整体思想得出∠AOB的度数是∠COE的度数的2倍.
题型四 借助一副三角板能画出的角的度数
例4 借助一副三角板，你能画出下面哪个度数的角？（ ）
A.65° B.75° C.80° D.95°
题型四 借助一副三角板能画出的角的度数
例4 借助一副三角板，你能画出下面哪个度数的角？（ ）
A.65° B.75° C.80° D.95°
解析 一副三角板中有30°、45°、60°、90°的角，所以能画出的最小角为45°-30°＝15°.所以15°的整数倍的角都能画出来.
因为75°是15°的整数倍，所以能画出来75°的角，故选B.
答案 B
易错易混
易错点 对角的“和”理解不透彻而导致漏解
例 已知在平面内，∠AOB＝70°，∠BOC＝40°，求∠AOC的度数.
解析 分∠BOC在∠AOB的外部和内部两种情况.
（1）当∠BOC在∠AOB的外部时，如图①所示，∠AOC＝∠AOB＋∠BOC＝70°＋40°＝110°；
（2）当∠BOC在∠AOB的内部时，如图②所示，∠AOC＝∠AOB-∠BOC＝70°-40°＝30°.
故∠AOC的度数为110°或30°.



解析 分∠BOC在∠AOB的外部和内部两种情况.
（1）当∠BOC在∠AOB的外部时，如图①所示，∠AOC＝∠AOB＋∠BOC＝70°＋40°＝110°；
（2）当∠BOC在∠AOB的内部时，如图②所示，∠AOC＝∠AOB-∠BOC＝70°-40°＝30°.
故∠AOC的度数为110°或30°.



易错警示
如果没有真正理解两角“和”的含义，也没有全面考虑具体图形（∠BOC可能在∠AOB的外部，也可能在∠AOB的内部），就可能会导致漏解.