6.1.2 算术平方根的估值 课件(共20张PPT)
文档属性
| 名称 | 6.1.2 算术平方根的估值 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-07 18:17:35 | ||
图片预览





文档简介
6.1.2 算术平方根的估值
第六章 实数
2021年春人教版七年级数学下册
1、会用计算器求一个数的算术平方根。
2、能用夹值法求一个数的算术平方根的近似值。
3、理解无限不循环小数的概念。
理解夹值法。(重点)
通过夹值法估计无理数的大小。( 难点)
学习目标
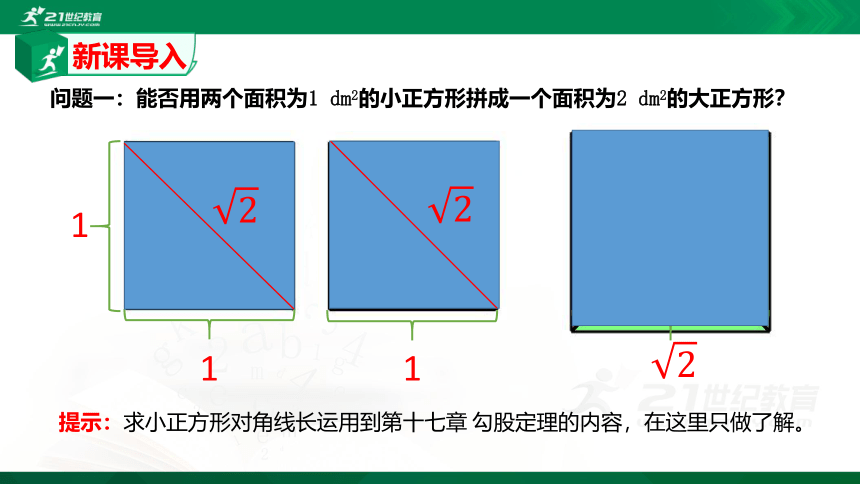
问题一:能否用两个面积为1 dm2的小正方形拼成一个面积为2 dm2的大正方形?
1
1
2
?
1
2
?
2
?
提示:求小正方形对角线长运用到第十七章 勾股定理的内容,在这里只做了解。
新课导入
2?有多大?
?
……
1)因为12=1, 22=4,而1< 2 <4,所以1< ?2? <2
?
2)因为1.42=1.96, 1.52=2.25,而1.96< 2 <2.25,所以1.4< 2?<1.5
?
3)因为1.412=1.9881, 1.422=2.0614,而1.9881< 2 <2.0614,所以1.41< 2?<1.42
?
4)因为1.4142=1.9999396, 1.4152=2.002225,
而1.999396< 2 <2.002225,所以1.414< 2?<1.415
?
探究新知
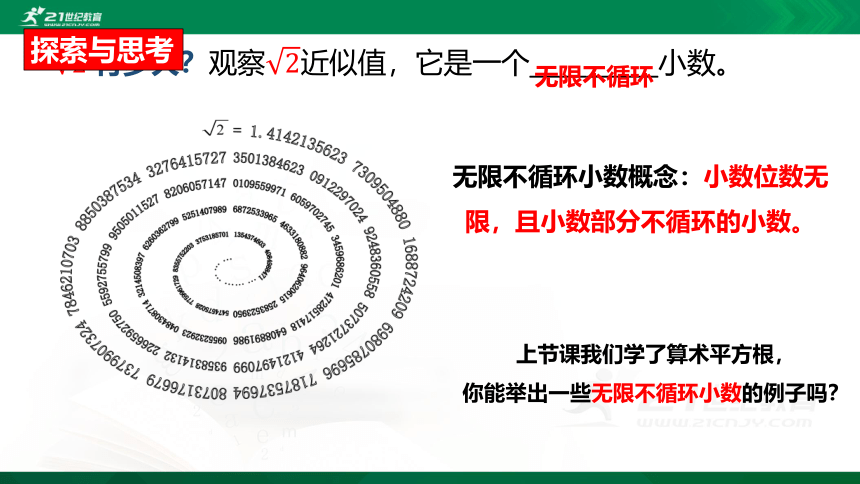
2?有多大?观察2近似值,它是一个_________小数。
?
无限不循环
无限不循环小数概念:小数位数无限,且小数部分不循环的小数。
上节课我们学了算术平方根,
你能举出一些无限不循环小数的例子吗?
探索与思考
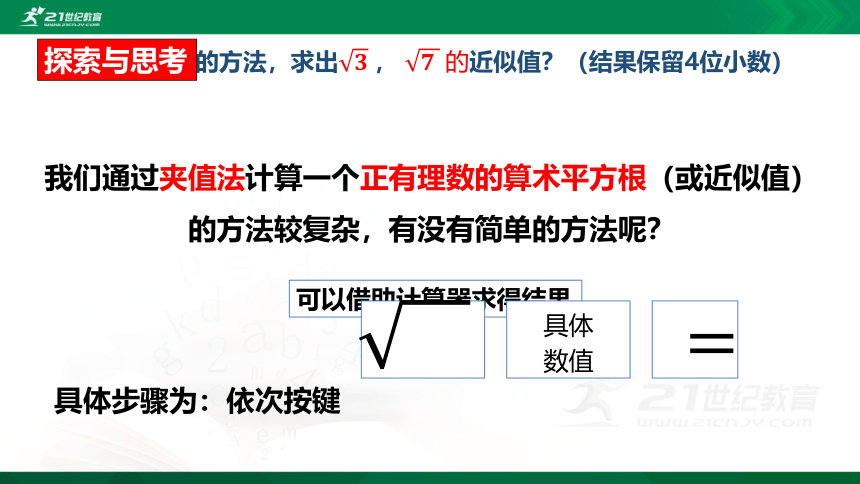
尝试通过上面的方法,求出?????, ??????的近似值?(结果保留4位小数)
?
我们通过夹值法计算一个正有理数的算术平方根(或近似值)
的方法较复杂,有没有简单的方法呢?
可以借助计算器求得结果
具体步骤为:依次按键
?
具体
数值
?
??=
?
探索与思考
用计算器求下列各式的值
1) ?????????????????
2)????(精确到0.01)
3) ????????????????
4)????????(精确到0.001)
5)????????(精确到0.0001)
?
(2)依次按键 2
显示:1.414213562.
∴ ????≈1.41.
?
解:(1)依次按键 3136
显示:56.
∴ 3136=56 .
?
针对练习
例题讲解
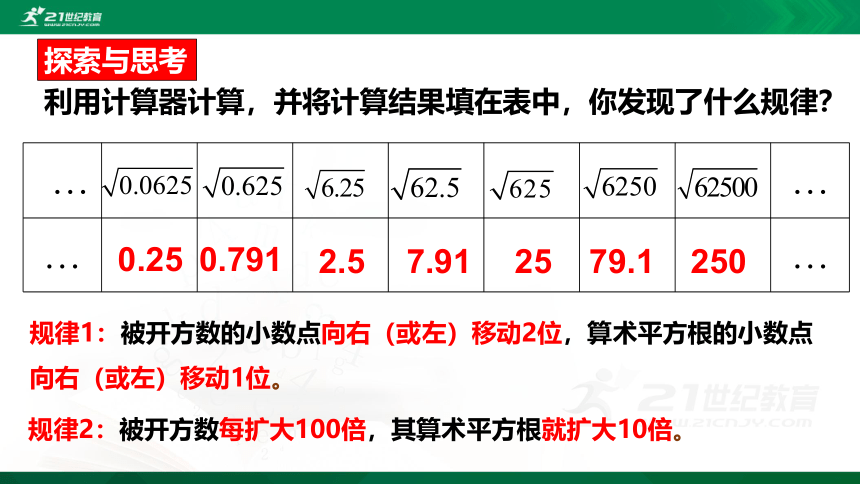
利用计算器计算,并将计算结果填在表中,你发现了什么规律?
…
…
…
…
0.25
0.791
2.5
7.91
25
79.1
250
规律1:被开方数的小数点向右(或左)移动2位,算术平方根的小数点向右(或左)移动1位。
规律2:被开方数每扩大100倍,其算术平方根就扩大10倍。
探索与思考
∵?????≈1.732
∴ ????.???????? ≈0. 1732,???????????? ≈17.32,?????????????????????≈173.2
?
用计算器计算????(精确到0.001),并利用刚才的得到规律说出????.????????, ???????????? , ????????????????????的近似值。你能否根据????的值说出????????是多少?
?
探索与思考
小丽想用一块面积为400cm2的正方形纸片,沿着边的方向剪出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2。她不知能否裁得出来,正在发愁。小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
【分析】
1、面积为400cm2的正方形纸片,它的边长为_______ cm;
2、若假设长方形的宽为2x,则长为____________ cm;
3、若这块这片符合要求,它的长和宽需要满足什么条件:
______________________________。
20
3x
3x<20,2x<20
例题讲解
小丽想用一块面积为400cm2的正方形纸片,沿着边的方向剪出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2。她不知能否裁得出来,正在发愁。小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
解:设长方形纸片的长为3x cm,宽为2x cm.根据边长与面积的关系得
3x ? 2x = 300 ,
解得 x = 50 ,
故长方形纸片的长为350 ,宽为250 .
?
因为50>49,得50 >7,所以350 >3×7=21,比原正方形的边长更长.
所以小丽不能用这块纸片裁出符合要求的纸片.
?
1.估算22的算术平方根在( )
A.2和3之间 B.3和4之间 C.4和5之间 D.5和6之间
【答案】C
【详解】
解:?∵16<24<25,
∴4<24<5,
∴24的算术平方根在4和5之间.
故选C.
?
课堂练习
变式1-1.面积为17m2的正方形,它的边长介于( )
A.2m与3m之间 B.3m与4m之间
C.4m与5m之间 D.5m与6m之间
【答案】C
【详解】
解:设正方形的边长为x,则x2=17,
∴x=17.
∵16<17<25,
∴4<17<5.
故选:C.
?
2.设n为正整数,且???? A.5 B.6 C.7 D.8
?
【答案】D
【解析】
试题分析:∵64<69<81,
∴8<69<9,
∵n<69<n+1(n为正整数),
∴n=8.
故选D.
?
变式2-1.若2<?????????<3,则a的值可以是( )
A.﹣7 B.???????????? C.???????????? D.12
?
【答案】C
【详解】
解:∵2<?????2<3,
∴4<a-2<9,∴6<a<11.
又a-2≥0,即a≥2.
∴a的取值范围是6<a<11.
观察选项,只有选项C符合题意.
故选C.
?
3.估计?????????????的值在( )
A.1到2之间 B.2到3之间 C.3到4之间 D.4到5之间
?
【答案】C
【解析】
∵16<17<25
∴4<17<5
∴3<17-1<4
因此17-1在3到4之间.
故选:C.
?
【答案】D
【详解】
∵2017≈44.91,∴20.17≈4.491.故选:D.
?
4.已知:????????????????≈44.91,????????????.????=14.0,则????????.????????的值约为( )
A.32.41 B.1.40
C.3.241 D.4.491
?
谢谢聆听
第六章 实数
2021年春人教版七年级数学下册
1、会用计算器求一个数的算术平方根。
2、能用夹值法求一个数的算术平方根的近似值。
3、理解无限不循环小数的概念。
理解夹值法。(重点)
通过夹值法估计无理数的大小。( 难点)
学习目标
问题一:能否用两个面积为1 dm2的小正方形拼成一个面积为2 dm2的大正方形?
1
1
2
?
1
2
?
2
?
提示:求小正方形对角线长运用到第十七章 勾股定理的内容,在这里只做了解。
新课导入
2?有多大?
?
……
1)因为12=1, 22=4,而1< 2 <4,所以1< ?2? <2
?
2)因为1.42=1.96, 1.52=2.25,而1.96< 2 <2.25,所以1.4< 2?<1.5
?
3)因为1.412=1.9881, 1.422=2.0614,而1.9881< 2 <2.0614,所以1.41< 2?<1.42
?
4)因为1.4142=1.9999396, 1.4152=2.002225,
而1.999396< 2 <2.002225,所以1.414< 2?<1.415
?
探究新知
2?有多大?观察2近似值,它是一个_________小数。
?
无限不循环
无限不循环小数概念:小数位数无限,且小数部分不循环的小数。
上节课我们学了算术平方根,
你能举出一些无限不循环小数的例子吗?
探索与思考
尝试通过上面的方法,求出?????, ??????的近似值?(结果保留4位小数)
?
我们通过夹值法计算一个正有理数的算术平方根(或近似值)
的方法较复杂,有没有简单的方法呢?
可以借助计算器求得结果
具体步骤为:依次按键
?
具体
数值
?
??=
?
探索与思考
用计算器求下列各式的值
1) ?????????????????
2)????(精确到0.01)
3) ????????????????
4)????????(精确到0.001)
5)????????(精确到0.0001)
?
(2)依次按键 2
显示:1.414213562.
∴ ????≈1.41.
?
解:(1)依次按键 3136
显示:56.
∴ 3136=56 .
?
针对练习
例题讲解
利用计算器计算,并将计算结果填在表中,你发现了什么规律?
…
…
…
…
0.25
0.791
2.5
7.91
25
79.1
250
规律1:被开方数的小数点向右(或左)移动2位,算术平方根的小数点向右(或左)移动1位。
规律2:被开方数每扩大100倍,其算术平方根就扩大10倍。
探索与思考
∵?????≈1.732
∴ ????.???????? ≈0. 1732,???????????? ≈17.32,?????????????????????≈173.2
?
用计算器计算????(精确到0.001),并利用刚才的得到规律说出????.????????, ???????????? , ????????????????????的近似值。你能否根据????的值说出????????是多少?
?
探索与思考
小丽想用一块面积为400cm2的正方形纸片,沿着边的方向剪出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2。她不知能否裁得出来,正在发愁。小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
【分析】
1、面积为400cm2的正方形纸片,它的边长为_______ cm;
2、若假设长方形的宽为2x,则长为____________ cm;
3、若这块这片符合要求,它的长和宽需要满足什么条件:
______________________________。
20
3x
3x<20,2x<20
例题讲解
小丽想用一块面积为400cm2的正方形纸片,沿着边的方向剪出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2。她不知能否裁得出来,正在发愁。小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
解:设长方形纸片的长为3x cm,宽为2x cm.根据边长与面积的关系得
3x ? 2x = 300 ,
解得 x = 50 ,
故长方形纸片的长为350 ,宽为250 .
?
因为50>49,得50 >7,所以350 >3×7=21,比原正方形的边长更长.
所以小丽不能用这块纸片裁出符合要求的纸片.
?
1.估算22的算术平方根在( )
A.2和3之间 B.3和4之间 C.4和5之间 D.5和6之间
【答案】C
【详解】
解:?∵16<24<25,
∴4<24<5,
∴24的算术平方根在4和5之间.
故选C.
?
课堂练习
变式1-1.面积为17m2的正方形,它的边长介于( )
A.2m与3m之间 B.3m与4m之间
C.4m与5m之间 D.5m与6m之间
【答案】C
【详解】
解:设正方形的边长为x,则x2=17,
∴x=17.
∵16<17<25,
∴4<17<5.
故选:C.
?
2.设n为正整数,且???? A.5 B.6 C.7 D.8
?
【答案】D
【解析】
试题分析:∵64<69<81,
∴8<69<9,
∵n<69<n+1(n为正整数),
∴n=8.
故选D.
?
变式2-1.若2<?????????<3,则a的值可以是( )
A.﹣7 B.???????????? C.???????????? D.12
?
【答案】C
【详解】
解:∵2<?????2<3,
∴4<a-2<9,∴6<a<11.
又a-2≥0,即a≥2.
∴a的取值范围是6<a<11.
观察选项,只有选项C符合题意.
故选C.
?
3.估计?????????????的值在( )
A.1到2之间 B.2到3之间 C.3到4之间 D.4到5之间
?
【答案】C
【解析】
∵16<17<25
∴4<17<5
∴3<17-1<4
因此17-1在3到4之间.
故选:C.
?
【答案】D
【详解】
∵2017≈44.91,∴20.17≈4.491.故选:D.
?
4.已知:????????????????≈44.91,????????????.????=14.0,则????????.????????的值约为( )
A.32.41 B.1.40
C.3.241 D.4.491
?
谢谢聆听
