6.1.3 平方根 课件(共16张PPT)
文档属性
| 名称 | 6.1.3 平方根 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-07 00:00:00 | ||
图片预览





文档简介
6.1.3
平方根
第六章
实数
2021年春人教版七年级数学下册
1、理解平方根的概念,会用符号表示一个数的平方根。
2、算术平方根与平方根的区别与联系。
3、会求一个数的平方根。
理解平方根的定义,会求一个数的平方根。(重点)
算术平方根与平方根的区别与联系。(
难点)
学习目标
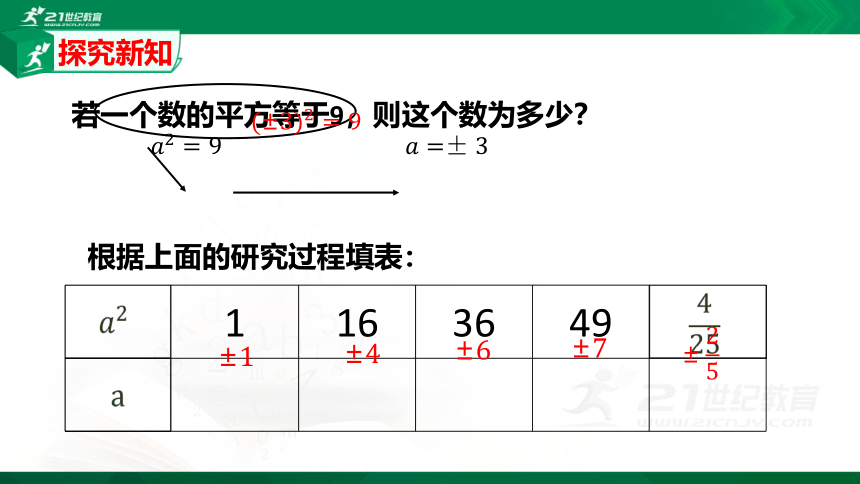
若一个数的平方等于9,则这个数为多少?
????2=9
?
(±3)2=9
?
????=±3
?
根据上面的研究过程填表:
1
16
36
49
±1
?
±4
?
±6
?
±7
?
±25
?
探究新知
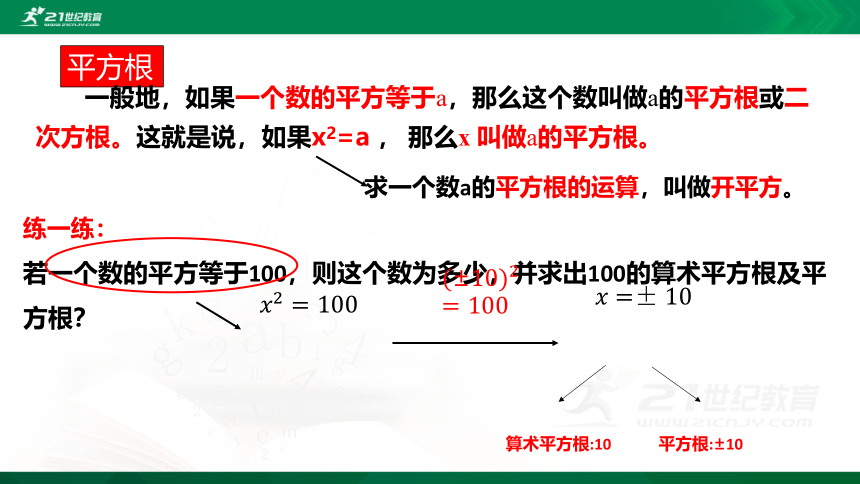
平方根
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根。这就是说,如果x2=a
,
那么x
叫做a的平方根。
求一个数a的平方根的运算,叫做开平方。
练一练:
若一个数的平方等于100,则这个数为多少,并求出100的算术平方根及平方根?
????2=100
?
(±10)2=100
?
????=±10
?
算术平方根:10
平方根:±10
探索平方与开平方的联系
{00A15C55-8517-42AA-B614-E9B94910E393}
1
4
16
平方
开平方
±1
?
±4
?
±2
?
1
?
1
?
4
?
4
?
16
?
16
?
观察表格的运算结果,你觉得平方与开平方之间有什么关系呢?
互逆运算
求下列各数的平方根
1)
????????????????2)????????????
3)0.36
4)
2????????
?
解:(1)因为(±13)2=169,所以169的平方根是±13.
(2)因为(±
????????)2=
?????????????,所以????????????的平方根是±
?????????.
?
(3)因为(±????.????)2
=
????.????????,所以????.????????的平方根是±????.????.
?
(4)因为(±????????)2
=214,所以214的平方根是±?????????.
?
针对练方根的表示
我们已经学过一个正数的算术平方根的表示方法,你能表示一个正数的平方根吗?
正数a的算术平方根
;
正数a的负的平方根
;
正数a的平方根
,
读作:正、负根号a
归纳小结
求下列各式的值
1)
????????????
2)
?????.??????????
3)
±????????????
?
解:(1)因为62=36,所以?????????=
6.
?
(2)因为0.92=
????.81,所以?????.??????????=
-0.9.
?
(3)因为(
????????
)2
=
?????????????,所以±?????????????=
±
????????
.
?
课堂练习
1.下列各数:64,?322,0,?4,??3,??3,??54,其中有平方根的有(
)
A.3个
B.4个
C.5个
D.6个
?
【答案】B
【详解】
解:?4、??3=-3、??54=-625,化简之后都为负数,64、?322、0、??3都为非负数,
∴有平方根的有4个.
故选B.
?
2.下列各式中,正确的是(
)
A.(?3)2=?3
B.?32=?3
C.(?3)2=?3
D.32=±3
?
【答案】B
【详解】
(?3)2=9=3;?32=?9=?3;(?3)2=32=3;
32=9=3,故选B.
?
3.下列运算中错误的有( )
①16=4②3649=±67,③?32=?3,④±32=3
A.4个
B.3个
C.2个
D.1个
?
【答案】B
【详解】
①16=4,;②3649=67,③?32,无法开方,;④±32=±3,.
错误的有3个.故选B.
?
4.若一个正数????的平方根为2?????7和14?3????,则????=(
)
A.7
B.16
C.25
D.49
?
【答案】D
【详解】
∵一个正数x的平方根为2?????7和14?3????,
∴(2?????7)+(14?3????)=0,解得:a=7.
∴2?????7=7,14?3????=-7,
∴x=(±7)2=49.
故选D.
?
5.若a2=4,b2=9,且ab<0,则a﹣b的值为( )
A.﹣2
B.±5
C.5
D.﹣5
【答案】B
【解析】
∵a2=4,b2=9,∴a=±2,b=±3,
∵ab<0,∴a=2时,b=?3,a?b=2?(?3)=2+3=5,
a=?2时,b=3,a?b=?2?3=?5,
所以,a?b的值为5或?5.
故选:B.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
算术平方根
平方根
区别
概念
表示方法
性质
1)正数只有一个算术平方根,且恒为正;
2)0的算术平方根为0
3)负数没有算术平方根
1)正数有两个平方根,且互为相反数;
2)0的平方根为0
3)负数没有平方根
求法
开平方后取非负的平方根
开平方
联系
1)a的取值范围相同,均为a≥0
2)平方根包含了算术平方根,即算术平方根是平方根中的一个(非负的)。
课堂小结
谢谢聆听
平方根
第六章
实数
2021年春人教版七年级数学下册
1、理解平方根的概念,会用符号表示一个数的平方根。
2、算术平方根与平方根的区别与联系。
3、会求一个数的平方根。
理解平方根的定义,会求一个数的平方根。(重点)
算术平方根与平方根的区别与联系。(
难点)
学习目标
若一个数的平方等于9,则这个数为多少?
????2=9
?
(±3)2=9
?
????=±3
?
根据上面的研究过程填表:
1
16
36
49
±1
?
±4
?
±6
?
±7
?
±25
?
探究新知
平方根
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根。这就是说,如果x2=a
,
那么x
叫做a的平方根。
求一个数a的平方根的运算,叫做开平方。
练一练:
若一个数的平方等于100,则这个数为多少,并求出100的算术平方根及平方根?
????2=100
?
(±10)2=100
?
????=±10
?
算术平方根:10
平方根:±10
探索平方与开平方的联系
{00A15C55-8517-42AA-B614-E9B94910E393}
1
4
16
平方
开平方
±1
?
±4
?
±2
?
1
?
1
?
4
?
4
?
16
?
16
?
观察表格的运算结果,你觉得平方与开平方之间有什么关系呢?
互逆运算
求下列各数的平方根
1)
????????????????2)????????????
3)0.36
4)
2????????
?
解:(1)因为(±13)2=169,所以169的平方根是±13.
(2)因为(±
????????)2=
?????????????,所以????????????的平方根是±
?????????.
?
(3)因为(±????.????)2
=
????.????????,所以????.????????的平方根是±????.????.
?
(4)因为(±????????)2
=214,所以214的平方根是±?????????.
?
针对练方根的表示
我们已经学过一个正数的算术平方根的表示方法,你能表示一个正数的平方根吗?
正数a的算术平方根
;
正数a的负的平方根
;
正数a的平方根
,
读作:正、负根号a
归纳小结
求下列各式的值
1)
????????????
2)
?????.??????????
3)
±????????????
?
解:(1)因为62=36,所以?????????=
6.
?
(2)因为0.92=
????.81,所以?????.??????????=
-0.9.
?
(3)因为(
????????
)2
=
?????????????,所以±?????????????=
±
????????
.
?
课堂练习
1.下列各数:64,?322,0,?4,??3,??3,??54,其中有平方根的有(
)
A.3个
B.4个
C.5个
D.6个
?
【答案】B
【详解】
解:?4、??3=-3、??54=-625,化简之后都为负数,64、?322、0、??3都为非负数,
∴有平方根的有4个.
故选B.
?
2.下列各式中,正确的是(
)
A.(?3)2=?3
B.?32=?3
C.(?3)2=?3
D.32=±3
?
【答案】B
【详解】
(?3)2=9=3;?32=?9=?3;(?3)2=32=3;
32=9=3,故选B.
?
3.下列运算中错误的有( )
①16=4②3649=±67,③?32=?3,④±32=3
A.4个
B.3个
C.2个
D.1个
?
【答案】B
【详解】
①16=4,;②3649=67,③?32,无法开方,;④±32=±3,.
错误的有3个.故选B.
?
4.若一个正数????的平方根为2?????7和14?3????,则????=(
)
A.7
B.16
C.25
D.49
?
【答案】D
【详解】
∵一个正数x的平方根为2?????7和14?3????,
∴(2?????7)+(14?3????)=0,解得:a=7.
∴2?????7=7,14?3????=-7,
∴x=(±7)2=49.
故选D.
?
5.若a2=4,b2=9,且ab<0,则a﹣b的值为( )
A.﹣2
B.±5
C.5
D.﹣5
【答案】B
【解析】
∵a2=4,b2=9,∴a=±2,b=±3,
∵ab<0,∴a=2时,b=?3,a?b=2?(?3)=2+3=5,
a=?2时,b=3,a?b=?2?3=?5,
所以,a?b的值为5或?5.
故选:B.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
算术平方根
平方根
区别
概念
表示方法
性质
1)正数只有一个算术平方根,且恒为正;
2)0的算术平方根为0
3)负数没有算术平方根
1)正数有两个平方根,且互为相反数;
2)0的平方根为0
3)负数没有平方根
求法
开平方后取非负的平方根
开平方
联系
1)a的取值范围相同,均为a≥0
2)平方根包含了算术平方根,即算术平方根是平方根中的一个(非负的)。
课堂小结
谢谢聆听
