五年级数学下册 一课一练《解决问题的策略》习题1-苏教版(含答案)
文档属性
| 名称 | 五年级数学下册 一课一练《解决问题的策略》习题1-苏教版(含答案) | 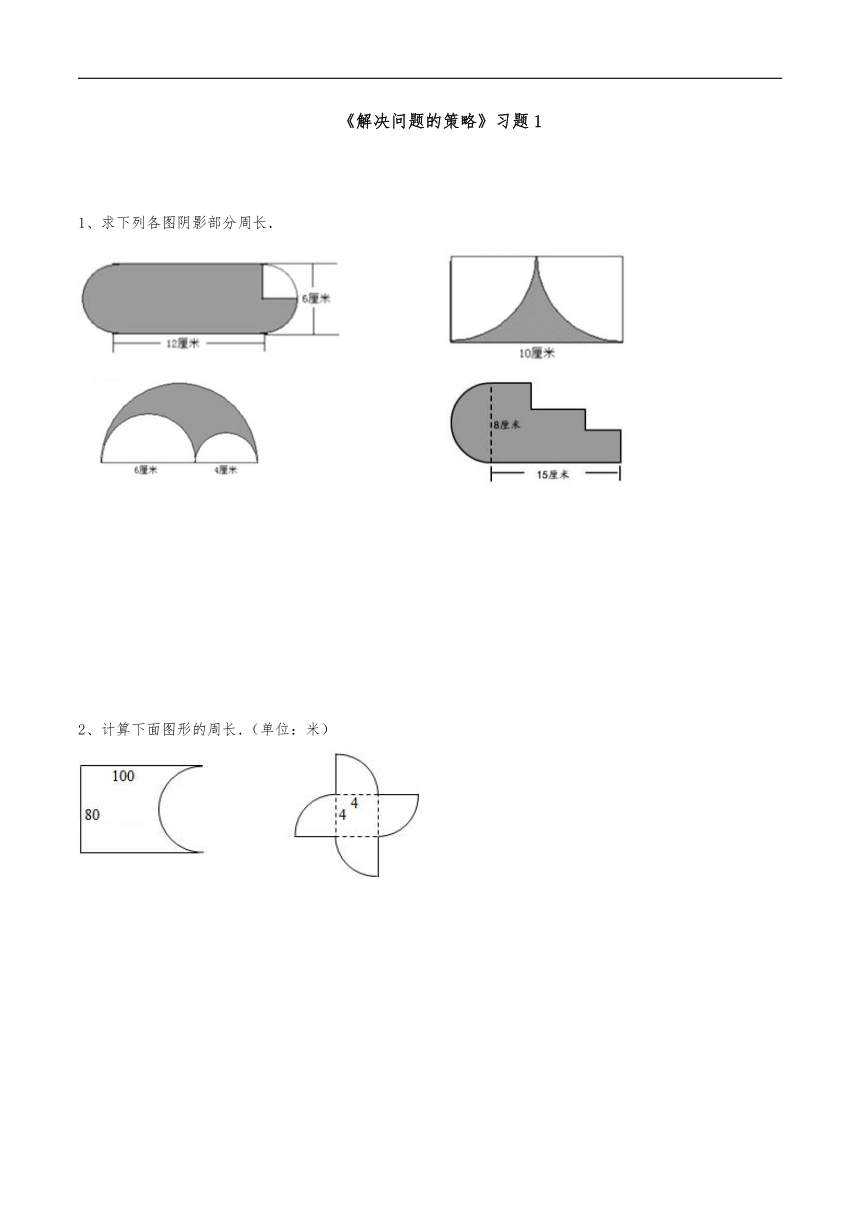 | |
| 格式 | zip | ||
| 文件大小 | 541.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-07 17:15:26 | ||
图片预览



文档简介
《解决问题的策略》习题1
1、求下列各图阴影部分周长.
2、计算下面图形的周长.(单位:米)
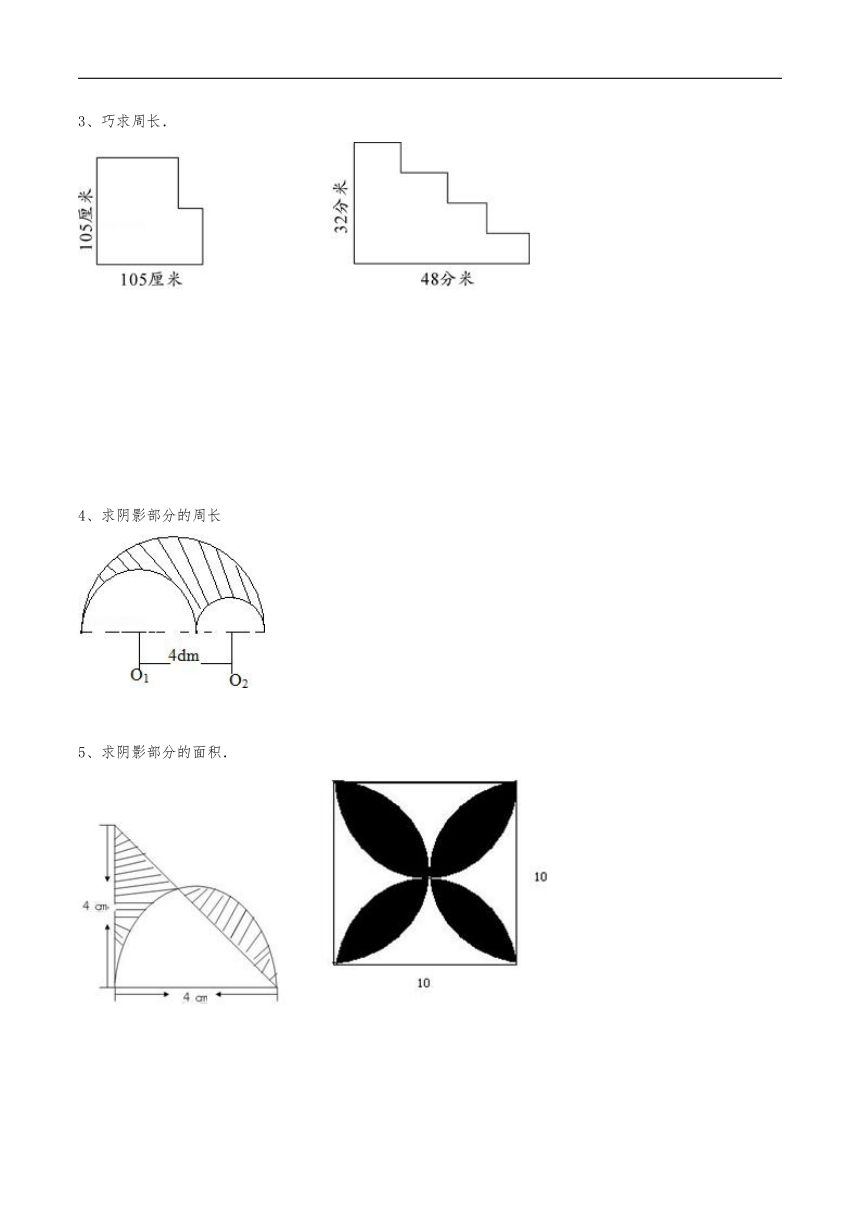
3、巧求周长.
4、求阴影部分的周长
5、求阴影部分的面积.
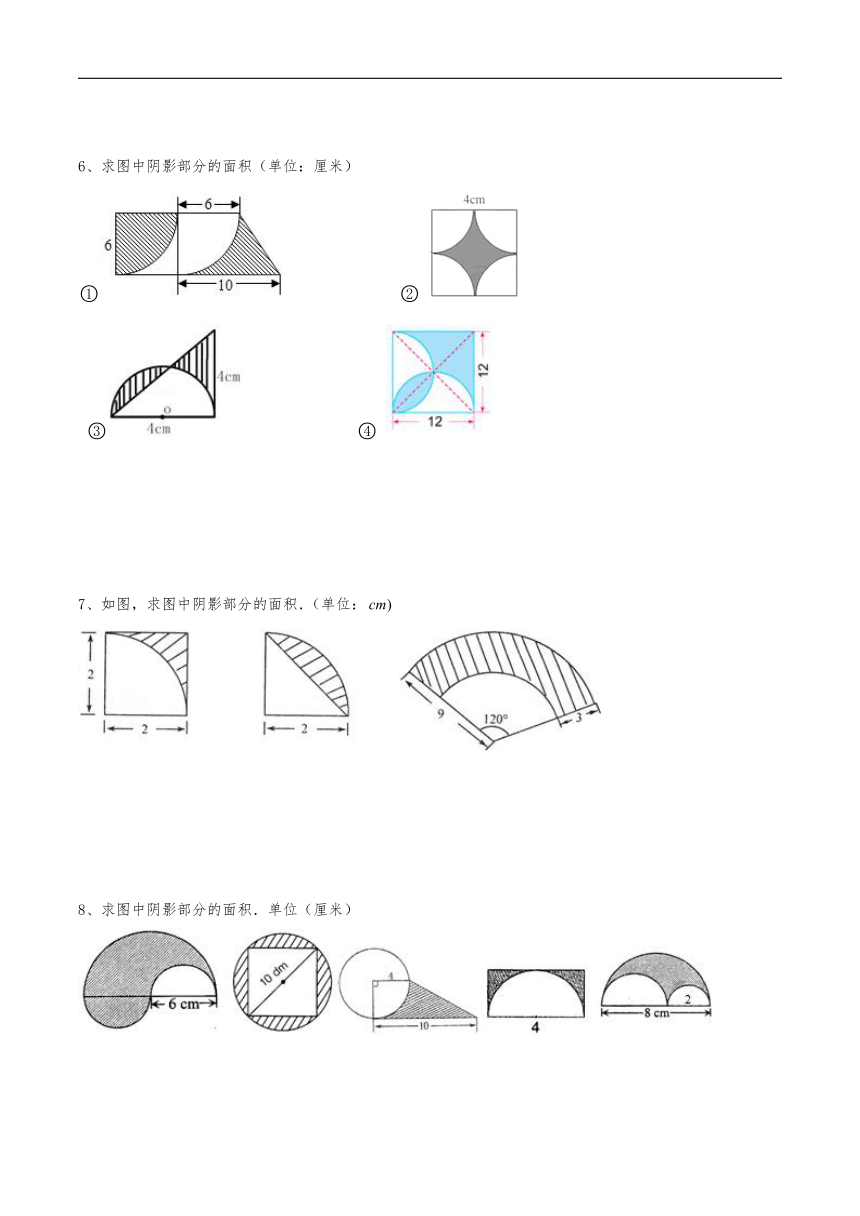
6、求图中阴影部分的面积(单位:厘米)
7、如图,求图中阴影部分的面积.(单位:
8、求图中阴影部分的面积.单位(厘米)
9、计算下面各题,想一想,怎样转化变形可以使计算更简便
.
;
10、计算:
.
11、高斯算法不神秘.
高斯被认为是历史上最重要的数学家之一,10岁时,他很快地做出了下面的题①.想想他用的运算定律,请你完成题②.
①
②
12、先找规律,再用简便方法计算.
答案
1、解:①
(厘米)
答:这个阴影部分的周长为44.13厘米.
②
(厘米)
答:这个阴影部分的周长为25.7厘米.
③
(厘米)
答:这个阴影部分的周长为31.4厘米.
④
(厘米)
答:阴影部分的周长是50.56厘米.
2、解:(1)
(米;
(2)
(米.
3、解:(1)(厘米)
答:这个图形的周长是420厘米.
(2)
(分米)
答:这个图形的周长是160分米.
4、解:
答:阴影部分的周长是.
5、解:(1)
(平方厘米);
答:阴影部分的面积是4平方厘米.
(2)
(平方厘米),
答:阴影部分的面积是57平方厘米.
6、解:
(平方厘米)
答:图中阴影部分的面积48平方厘米.
(平方厘米)
答:阴影部分的面积是3.44平方厘米.
(平方厘米)
答:阴影部分的面积是3.44平方厘米.
(平方厘米)
答:阴影部分的面积是4平方厘米
7、解:(1),
,
;
(2),
,
;
(3),
,
,
;
答:阴影部分的面积从左到右分别是,,.
8、解:(1)
答:阴影部分面积是.
(2)
答:阴影部分面积是.
(3)
答:阴影部分面积是.
(4)
答:阴影部分面积是.
(5)
答:阴影部分面积是.
9、解:
,
,
,
.
10、解:①
②
.
.
11、解:
12、解:
;
.
1、求下列各图阴影部分周长.
2、计算下面图形的周长.(单位:米)
3、巧求周长.
4、求阴影部分的周长
5、求阴影部分的面积.
6、求图中阴影部分的面积(单位:厘米)
7、如图,求图中阴影部分的面积.(单位:
8、求图中阴影部分的面积.单位(厘米)
9、计算下面各题,想一想,怎样转化变形可以使计算更简便
.
;
10、计算:
.
11、高斯算法不神秘.
高斯被认为是历史上最重要的数学家之一,10岁时,他很快地做出了下面的题①.想想他用的运算定律,请你完成题②.
①
②
12、先找规律,再用简便方法计算.
答案
1、解:①
(厘米)
答:这个阴影部分的周长为44.13厘米.
②
(厘米)
答:这个阴影部分的周长为25.7厘米.
③
(厘米)
答:这个阴影部分的周长为31.4厘米.
④
(厘米)
答:阴影部分的周长是50.56厘米.
2、解:(1)
(米;
(2)
(米.
3、解:(1)(厘米)
答:这个图形的周长是420厘米.
(2)
(分米)
答:这个图形的周长是160分米.
4、解:
答:阴影部分的周长是.
5、解:(1)
(平方厘米);
答:阴影部分的面积是4平方厘米.
(2)
(平方厘米),
答:阴影部分的面积是57平方厘米.
6、解:
(平方厘米)
答:图中阴影部分的面积48平方厘米.
(平方厘米)
答:阴影部分的面积是3.44平方厘米.
(平方厘米)
答:阴影部分的面积是3.44平方厘米.
(平方厘米)
答:阴影部分的面积是4平方厘米
7、解:(1),
,
;
(2),
,
;
(3),
,
,
;
答:阴影部分的面积从左到右分别是,,.
8、解:(1)
答:阴影部分面积是.
(2)
答:阴影部分面积是.
(3)
答:阴影部分面积是.
(4)
答:阴影部分面积是.
(5)
答:阴影部分面积是.
9、解:
,
,
,
.
10、解:①
②
.
.
11、解:
12、解:
;
.
