7.1.1 有序数对 课件(共22张PPT)
文档属性
| 名称 | 7.1.1 有序数对 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-07 18:14:00 | ||
图片预览






文档简介
7.1.1有序数对
2021年春人教版七年级数学下册
第七章 平面直角坐标系
1.了解有序数对的概念.
2.结合实例进一步体会有序数对的意义,并会用有序数对表示物体的位置.
学习目标
张亮父子俩周末去电影院看国产大片《红海行动》,买了两张票去观看,座位号分别是5排6号和6排5号.怎样才能既快又准地找到座位?
新课导入
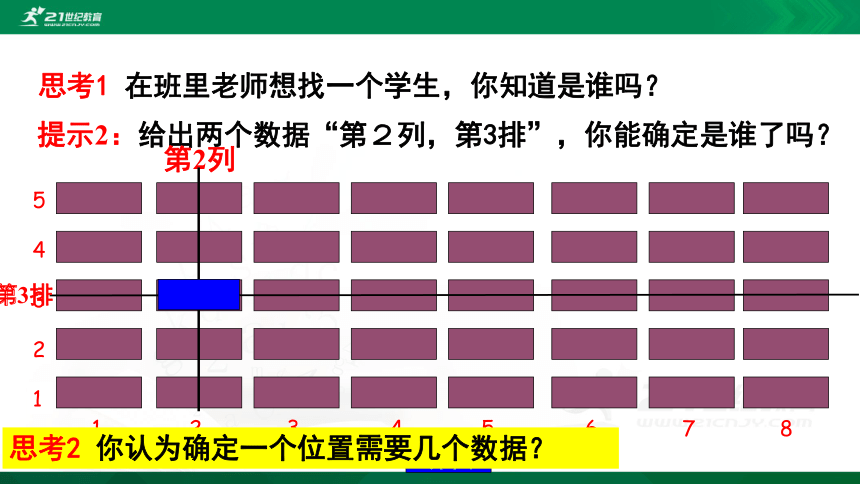
思考1 在班里老师想找一个学生,你知道是谁吗?
提示1:只给一个数据“第2列”,你能确定老师要找的学生是谁吗?
探究新知
思考1 在班里老师想找一个学生,你知道是谁吗?
提示2:给出两个数据“第2列,第3排”,你能确定是谁了吗?
讲台
2
1
3
4
5
6
7
8
1
2
3
4
5
第2列
思考2 你认为确定一个位置需要几个数据?
第3排
讲台
2
1
3
4
5
6
7
8
1
2
3
4
5
第3排
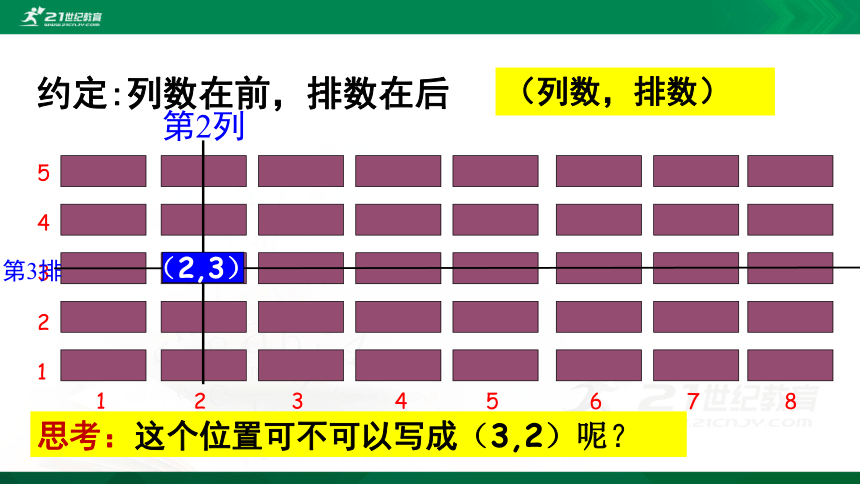
第2列
(2,3)
(列数,排数)
约定:列数在前,排数在后
思考:这个位置可不可以写成(3,2)呢?
我们把这种有顺序的两个数a与b组成的数对,叫做有序数对.记做(a, b).
有序数对的概念
注意:(a,b)与( b,a)是两个不同的数据.
归纳小结
1,“怪兽吃豆豆”是一种计算机游戏,图中的●标志表示“怪兽”先后经过的几个位置,如果用(1,2)表示“怪兽”经过的第2个位置,那么你能用同样的方式表示出图中“怪兽”经过的其他几个位置吗?
1
2
3
4
5
1
2
3
4
5
6
7
8
排
列
(3,2)
(4,3)
(3,3)
(4,5)
(5,4)
(5,5)
(7,4)
(7,3)
(8,3)
(1,1)
(1,2)
针对练习
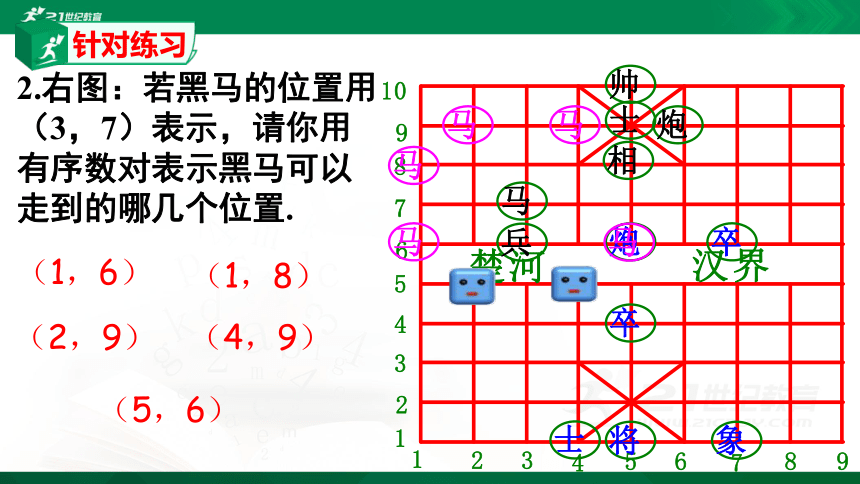
2.右图:若黑马的位置用(3,7)表示,请你用有序数对表示黑马可以走到的哪几个位置.
(1,6)
(1,8)
(2,9)
(4,9)
(5,6)
针对练习
从市五十二中到碧沙岗的距离大约是3.2公里,你能告诉游客如何在手机上找到打车软件——“滴滴出行”为游客叫车吗?
你能举例在生活中用有序数对表示位置的例子吗?
探索思考
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
13 12 11 10 9 8 7 6 5 4 3 2 1
A
C
D
E
F
G
若A(2,1)(1)图中五角星五个顶点的位置如何表示?
C点是(7,10)
D点是(3,7)
E点是(4,2)
F点是(10,2)
G点是(11,7)
针对练习
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
13 12 11 10 9 8 7 6 5 4 3 2 1
A
C
D
E
F
G
(2),图中(6,1),(10,8),位置上分别是什么物体?
分别表示足球和草莓
思考:在地球上如何确定城市的位置?
在地球上有横线和竖线,连接两极点的竖线叫经线,垂直于经线的横线圈为纬线.根据经纬线可以确定地球上任何一点的正确位置.
探索思考
哈尔滨的位置:
北纬:46°
东经:126°
,
针对练习
据新华社报道,2008年5月12日 14:28,我国四川省发生里氏8.0级强烈地震,震中位于阿坝州汶川县境内,即北纬31?,东经 103.4 ?.这是新中国成立以来破坏最强、波及范围最大的一次地震.你能在地图上找到震中的大致位置吗?
1.这是某班几个同学写出来的几个有序数对,谁写对了?
A (5、9)
B (x,y)
E (b,9)
C 4,6
D (a b)
×
√
×
×
√
F (3;a)
×
课堂练习
1街 2街 3街 4街 5街 6街
A
B
(3,5)
(3,4)
(3,3)
(4,3)
(5,3)
2. 如图,点A表示3街与5大道的十字路口,点B表示5街与3大道的十字路口.如果用(3,5)----(4,5) ---- (5,5) ---- (5,3)表示由A到B的一条林荫道,那么你能用同样的方式写出由A到B的其他路径吗?
5
预
明
满
万
次
4
中
活
此
成
学
3
祝
英
天
!
动
2
球
里
区
生
大
1
功
片
打
习
圆
A
B
C
D
E
3.如右图,方块中用(C,3)表示“天”,那么按下列要求排列会组成一句什么话,把它读出来.
(A,5 ) (A,3) (C,4 ) (E,5 ) (B,1) (C,2) (B,4)
(E,3) (E,1) (C,5) (D,4) (A,1) (D,3)
预
祝
此
次
片
区
活
动
圆
满
成
功
!
8
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
9
10
●
●
●
●
●
●
●
●
大门
食堂
宿舍楼
宣传橱窗
实验楼
教学楼
运动场
办公楼
(9,6)
(8,5)
(3,7)
(6,8)
(7,4)
(2,2)
(3,3)
(5,2)
4.已知大门的位置,用有序数对表示学校里的各个地点.
有序数对
点的位置
思想方法:
我们把这种有顺序的两个数a与b组成的数对,叫做有序数对.记做(a, b).
有序数对的概念
注意:(a,b)与( b,a)是两个不同的数据.
课堂小结
谢谢聆听
2021年春人教版七年级数学下册
第七章 平面直角坐标系
1.了解有序数对的概念.
2.结合实例进一步体会有序数对的意义,并会用有序数对表示物体的位置.
学习目标
张亮父子俩周末去电影院看国产大片《红海行动》,买了两张票去观看,座位号分别是5排6号和6排5号.怎样才能既快又准地找到座位?
新课导入
思考1 在班里老师想找一个学生,你知道是谁吗?
提示1:只给一个数据“第2列”,你能确定老师要找的学生是谁吗?
探究新知
思考1 在班里老师想找一个学生,你知道是谁吗?
提示2:给出两个数据“第2列,第3排”,你能确定是谁了吗?
讲台
2
1
3
4
5
6
7
8
1
2
3
4
5
第2列
思考2 你认为确定一个位置需要几个数据?
第3排
讲台
2
1
3
4
5
6
7
8
1
2
3
4
5
第3排
第2列
(2,3)
(列数,排数)
约定:列数在前,排数在后
思考:这个位置可不可以写成(3,2)呢?
我们把这种有顺序的两个数a与b组成的数对,叫做有序数对.记做(a, b).
有序数对的概念
注意:(a,b)与( b,a)是两个不同的数据.
归纳小结
1,“怪兽吃豆豆”是一种计算机游戏,图中的●标志表示“怪兽”先后经过的几个位置,如果用(1,2)表示“怪兽”经过的第2个位置,那么你能用同样的方式表示出图中“怪兽”经过的其他几个位置吗?
1
2
3
4
5
1
2
3
4
5
6
7
8
排
列
(3,2)
(4,3)
(3,3)
(4,5)
(5,4)
(5,5)
(7,4)
(7,3)
(8,3)
(1,1)
(1,2)
针对练习
2.右图:若黑马的位置用(3,7)表示,请你用有序数对表示黑马可以走到的哪几个位置.
(1,6)
(1,8)
(2,9)
(4,9)
(5,6)
针对练习
从市五十二中到碧沙岗的距离大约是3.2公里,你能告诉游客如何在手机上找到打车软件——“滴滴出行”为游客叫车吗?
你能举例在生活中用有序数对表示位置的例子吗?
探索思考
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
13 12 11 10 9 8 7 6 5 4 3 2 1
A
C
D
E
F
G
若A(2,1)(1)图中五角星五个顶点的位置如何表示?
C点是(7,10)
D点是(3,7)
E点是(4,2)
F点是(10,2)
G点是(11,7)
针对练习
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
13 12 11 10 9 8 7 6 5 4 3 2 1
A
C
D
E
F
G
(2),图中(6,1),(10,8),位置上分别是什么物体?
分别表示足球和草莓
思考:在地球上如何确定城市的位置?
在地球上有横线和竖线,连接两极点的竖线叫经线,垂直于经线的横线圈为纬线.根据经纬线可以确定地球上任何一点的正确位置.
探索思考
哈尔滨的位置:
北纬:46°
东经:126°
,
针对练习
据新华社报道,2008年5月12日 14:28,我国四川省发生里氏8.0级强烈地震,震中位于阿坝州汶川县境内,即北纬31?,东经 103.4 ?.这是新中国成立以来破坏最强、波及范围最大的一次地震.你能在地图上找到震中的大致位置吗?
1.这是某班几个同学写出来的几个有序数对,谁写对了?
A (5、9)
B (x,y)
E (b,9)
C 4,6
D (a b)
×
√
×
×
√
F (3;a)
×
课堂练习
1街 2街 3街 4街 5街 6街
A
B
(3,5)
(3,4)
(3,3)
(4,3)
(5,3)
2. 如图,点A表示3街与5大道的十字路口,点B表示5街与3大道的十字路口.如果用(3,5)----(4,5) ---- (5,5) ---- (5,3)表示由A到B的一条林荫道,那么你能用同样的方式写出由A到B的其他路径吗?
5
预
明
满
万
次
4
中
活
此
成
学
3
祝
英
天
!
动
2
球
里
区
生
大
1
功
片
打
习
圆
A
B
C
D
E
3.如右图,方块中用(C,3)表示“天”,那么按下列要求排列会组成一句什么话,把它读出来.
(A,5 ) (A,3) (C,4 ) (E,5 ) (B,1) (C,2) (B,4)
(E,3) (E,1) (C,5) (D,4) (A,1) (D,3)
预
祝
此
次
片
区
活
动
圆
满
成
功
!
8
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
9
10
●
●
●
●
●
●
●
●
大门
食堂
宿舍楼
宣传橱窗
实验楼
教学楼
运动场
办公楼
(9,6)
(8,5)
(3,7)
(6,8)
(7,4)
(2,2)
(3,3)
(5,2)
4.已知大门的位置,用有序数对表示学校里的各个地点.
有序数对
点的位置
思想方法:
我们把这种有顺序的两个数a与b组成的数对,叫做有序数对.记做(a, b).
有序数对的概念
注意:(a,b)与( b,a)是两个不同的数据.
课堂小结
谢谢聆听
