7.1.2平面直角坐标系(平面直角坐标系相关概念) 课件(共21张)
文档属性
| 名称 | 7.1.2平面直角坐标系(平面直角坐标系相关概念) 课件(共21张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-07 18:05:37 | ||
图片预览





文档简介
7.1.2平面直角坐标系(平面直角坐标系相关概念)
2021年春人教版七年级数学下册
第七章 平面直角坐标系
1,理解平面直角坐标系的相关概念。
2,能在平面直角坐标系中,根据坐标找出点,由点描出坐标。
3,平面直角坐标系四个象限和坐标轴上点的坐标特征。
学习目标
思考:什么叫做有序数对?
把有顺序的两个数a与b组成的数对叫做有序数对。记做(a,b)
思考:你呢个举出一些例子吗?
(1,5),(5,1),(2,4),(4,2),(3,5),(5,3)
新课导入
数轴的三要素:原点、正方向、单位长度。
思考:数轴上的点与实数是一一对应的。
类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置呢?
平面直角坐标系
新课导入
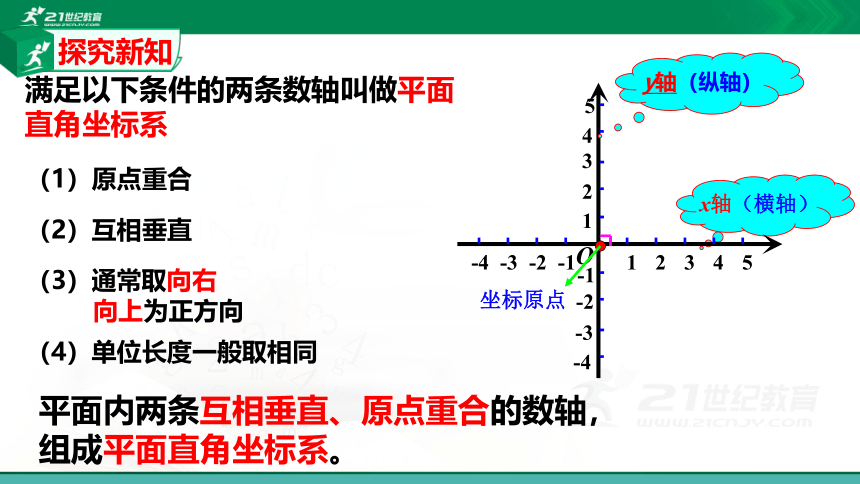
满足以下条件的两条数轴叫做平面直角坐标系
(1)原点重合
(2)互相垂直
x轴(横轴)
O
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y轴(纵轴)
坐标原点
(3)通常取向右
向上为正方向
(4)单位长度一般取相同
平面内两条互相垂直、原点重合的数轴,
组成平面直角坐标系。
探究新知
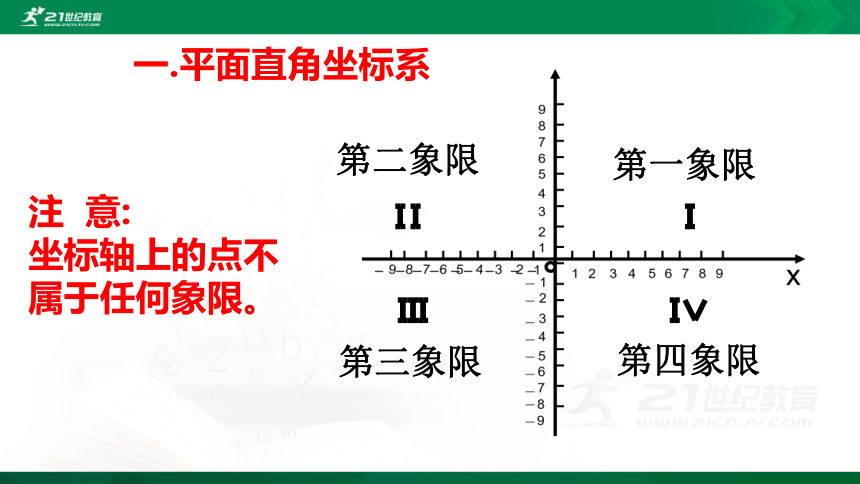
一.平面直角坐标系
第二象限
第一象限
第三象限
第四象限
注 意:
坐标轴上的点不属于任何象限。
y
-5
-6
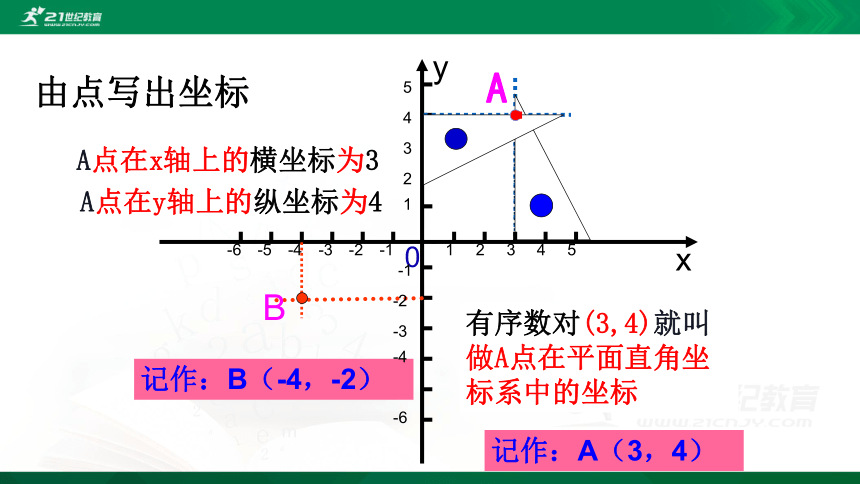
A点在y轴上的纵坐标为4
A点在x轴上的横坐标为3
有序数对(3,4)就叫做A点在平面直角坐标系中的坐标
记作:B(-4,-2)
x
0
1
2
3
4
5
-1
-2
-3
-4
-5
-6
1
2
3
4
5
-1
-2
-3
-4
A
B
.
记作:A(3,4)
由点写出坐标
·
B
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
C
·
A
·
E
·
D
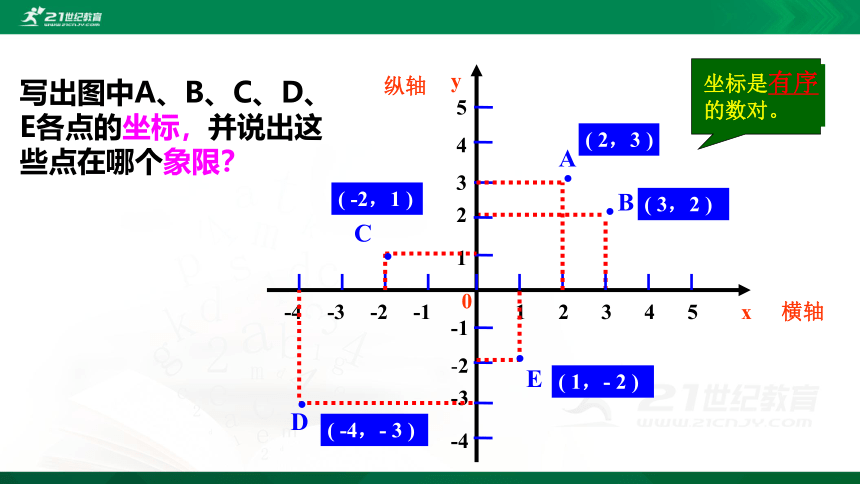
( 2,3 )
( 3,2 )
( -2,1 )
( -4,- 3 )
( 1,- 2 )
坐标是有序
的数对。
写出图中A、B、C、D、E各点的坐标,并说出这些点在哪个象限?
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
在平面直角坐标系中 找(3,-2)表示的点A。
由坐标找点的方法:
先找到表示横坐标与纵坐标的点,
然后过这两点分别作x轴与y轴的垂线,
垂线的交点就是该坐标对应的点。
A
由坐标找点
3
1
2
-2
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
·
P
点P(a,b)分别在四个象限时,横、纵坐标有什么特征?
·
P
·
P
·
P
(+,+)
(-,+)
(-,-)
(+,-)
x
y
即:a>0
b>0
即:a<0
b>0
即:a<0
b<0
即:a>0
b<0
探索思考
探究1:
找出图中各点的坐标:
A ( , )
B ( , )
C ( , )
D ( , )
O ( , )
-3
0
2
0
0
-2
3
0
坐标轴上点的坐标特点
O
-1
-2
-3
1
2
3
1
2
3
-1
-2
-3
x
4
y
A
B
D
C
0
0
X 轴上点坐标横坐标是任意实数,纵坐标为0。
y轴上点的坐标横坐标为0,纵坐标是任意实数。
探究2:
探索思考
点的位置
横坐标符号
纵坐标符号
第一象限
第二象限
第三象限
第四象限
X轴
正半轴
负半轴
Y轴
正半轴
负半轴
原点
+
+
+
+
—
—
—
—
—
—
0
0
0
0
0
0
+
+
归纳小结
②描出(-2,2),
(0,2),
(2,2),
(4,2),
依次连接各点, 发现了什么?
①描出(2,3),
(2,2),
(2,0),
(2,-2),
依次连接各点, 发现了什么?
0
x
y
横坐标相同点的连线,平行于y轴
纵坐标相同点的连线,平行于x轴
探究3:
探索思考
1.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( )
(A)平行于x轴 (B)平行于y轴
(C)经过原点 (D)以上都不对
B
2.已知点 P( a,b),Q(3,6)且 PQ∥x轴,则 b的值为_______
6
例题讲解
3.平行于横轴的直线上的点的_______相同;
平行于纵轴的直线上的点的_______相同;
4.已知点M(3a-2,a+6),点N的坐标为(2,5)且直线MN∥x轴,求点M的坐标。
纵坐标
横坐标
(-5,5)
3
1
2
-2
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
当点P落在一、三象限的两条坐标轴夹角平分线上时,点P(a,b)具有什么特征?
x
y
(a,a)
·
P
·
P
a=b
探究4:
探索思考
3
1
2
-2
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
当点P落在二、四象限的两条坐标轴夹角平分线上时,点P(a,b)具有什么特征?
x
y
·
P
·
P
(a,-a)
a=-b
探究5:
探索思考
若点A(a,b)在第三象限,则点 Q
(-a+1,b-5)在第( )象限。
2. 若点B(m+4,m-1)在X轴上,则m=______。
3. 若点 C(x,y)满足x+y<0 , xy >0 ,
则点C在第( )象限。
4. 若点D(6-5m,m2-2)在第二、四象限夹角
的平分线上,则m=( )。
四
1
三
1或4
课堂练习
1、平面直角坐标系的概念。
2、能在平面直角坐标系中,根据坐标找出点,由点描出坐标。坐标平面内的点与有序实数对是一一 对应的。
3、平面直角坐标系四个象限和坐标轴上点的坐标特征。
4、坐标轴的夹角平分线的点的坐标特征。
课堂小结
谢谢聆听
2021年春人教版七年级数学下册
第七章 平面直角坐标系
1,理解平面直角坐标系的相关概念。
2,能在平面直角坐标系中,根据坐标找出点,由点描出坐标。
3,平面直角坐标系四个象限和坐标轴上点的坐标特征。
学习目标
思考:什么叫做有序数对?
把有顺序的两个数a与b组成的数对叫做有序数对。记做(a,b)
思考:你呢个举出一些例子吗?
(1,5),(5,1),(2,4),(4,2),(3,5),(5,3)
新课导入
数轴的三要素:原点、正方向、单位长度。
思考:数轴上的点与实数是一一对应的。
类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置呢?
平面直角坐标系
新课导入
满足以下条件的两条数轴叫做平面直角坐标系
(1)原点重合
(2)互相垂直
x轴(横轴)
O
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y轴(纵轴)
坐标原点
(3)通常取向右
向上为正方向
(4)单位长度一般取相同
平面内两条互相垂直、原点重合的数轴,
组成平面直角坐标系。
探究新知
一.平面直角坐标系
第二象限
第一象限
第三象限
第四象限
注 意:
坐标轴上的点不属于任何象限。
y
-5
-6
A点在y轴上的纵坐标为4
A点在x轴上的横坐标为3
有序数对(3,4)就叫做A点在平面直角坐标系中的坐标
记作:B(-4,-2)
x
0
1
2
3
4
5
-1
-2
-3
-4
-5
-6
1
2
3
4
5
-1
-2
-3
-4
A
B
.
记作:A(3,4)
由点写出坐标
·
B
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
C
·
A
·
E
·
D
( 2,3 )
( 3,2 )
( -2,1 )
( -4,- 3 )
( 1,- 2 )
坐标是有序
的数对。
写出图中A、B、C、D、E各点的坐标,并说出这些点在哪个象限?
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
在平面直角坐标系中 找(3,-2)表示的点A。
由坐标找点的方法:
先找到表示横坐标与纵坐标的点,
然后过这两点分别作x轴与y轴的垂线,
垂线的交点就是该坐标对应的点。
A
由坐标找点
3
1
2
-2
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
·
P
点P(a,b)分别在四个象限时,横、纵坐标有什么特征?
·
P
·
P
·
P
(+,+)
(-,+)
(-,-)
(+,-)
x
y
即:a>0
b>0
即:a<0
b>0
即:a<0
b<0
即:a>0
b<0
探索思考
探究1:
找出图中各点的坐标:
A ( , )
B ( , )
C ( , )
D ( , )
O ( , )
-3
0
2
0
0
-2
3
0
坐标轴上点的坐标特点
O
-1
-2
-3
1
2
3
1
2
3
-1
-2
-3
x
4
y
A
B
D
C
0
0
X 轴上点坐标横坐标是任意实数,纵坐标为0。
y轴上点的坐标横坐标为0,纵坐标是任意实数。
探究2:
探索思考
点的位置
横坐标符号
纵坐标符号
第一象限
第二象限
第三象限
第四象限
X轴
正半轴
负半轴
Y轴
正半轴
负半轴
原点
+
+
+
+
—
—
—
—
—
—
0
0
0
0
0
0
+
+
归纳小结
②描出(-2,2),
(0,2),
(2,2),
(4,2),
依次连接各点, 发现了什么?
①描出(2,3),
(2,2),
(2,0),
(2,-2),
依次连接各点, 发现了什么?
0
x
y
横坐标相同点的连线,平行于y轴
纵坐标相同点的连线,平行于x轴
探究3:
探索思考
1.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( )
(A)平行于x轴 (B)平行于y轴
(C)经过原点 (D)以上都不对
B
2.已知点 P( a,b),Q(3,6)且 PQ∥x轴,则 b的值为_______
6
例题讲解
3.平行于横轴的直线上的点的_______相同;
平行于纵轴的直线上的点的_______相同;
4.已知点M(3a-2,a+6),点N的坐标为(2,5)且直线MN∥x轴,求点M的坐标。
纵坐标
横坐标
(-5,5)
3
1
2
-2
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
当点P落在一、三象限的两条坐标轴夹角平分线上时,点P(a,b)具有什么特征?
x
y
(a,a)
·
P
·
P
a=b
探究4:
探索思考
3
1
2
-2
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
当点P落在二、四象限的两条坐标轴夹角平分线上时,点P(a,b)具有什么特征?
x
y
·
P
·
P
(a,-a)
a=-b
探究5:
探索思考
若点A(a,b)在第三象限,则点 Q
(-a+1,b-5)在第( )象限。
2. 若点B(m+4,m-1)在X轴上,则m=______。
3. 若点 C(x,y)满足x+y<0 , xy >0 ,
则点C在第( )象限。
4. 若点D(6-5m,m2-2)在第二、四象限夹角
的平分线上,则m=( )。
四
1
三
1或4
课堂练习
1、平面直角坐标系的概念。
2、能在平面直角坐标系中,根据坐标找出点,由点描出坐标。坐标平面内的点与有序实数对是一一 对应的。
3、平面直角坐标系四个象限和坐标轴上点的坐标特征。
4、坐标轴的夹角平分线的点的坐标特征。
课堂小结
谢谢聆听
