7.1.2平面直角坐标系(2)点的坐标特点 课件(共16张PPT)
文档属性
| 名称 | 7.1.2平面直角坐标系(2)点的坐标特点 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-07 18:02:35 | ||
图片预览




文档简介
7.1.2 平面直角坐标系(第二课时)
2021年春人教版七年级数学下册
第七章 平面直角坐标系
1,如何求点到坐标轴的距离?
2,关于坐标轴对称的点的坐标特征。
学习目标
2.已知P点坐标为(a+1,a-3)
①点P在x轴上,则a = ;
②点P在y轴上,则a = ;
3.若点P(x,y)在第四象限,|x|=5,|y|=4,则P点的坐标为__________。
3
(5,-4)
-1
1.已知a二
变式:若点P(x,y)中,|x|=5,|y|=4,则P点的坐标为_______________________________________________。
(5,4)或(5,-4)或(-5,4)或(-5,-4)
复习巩固
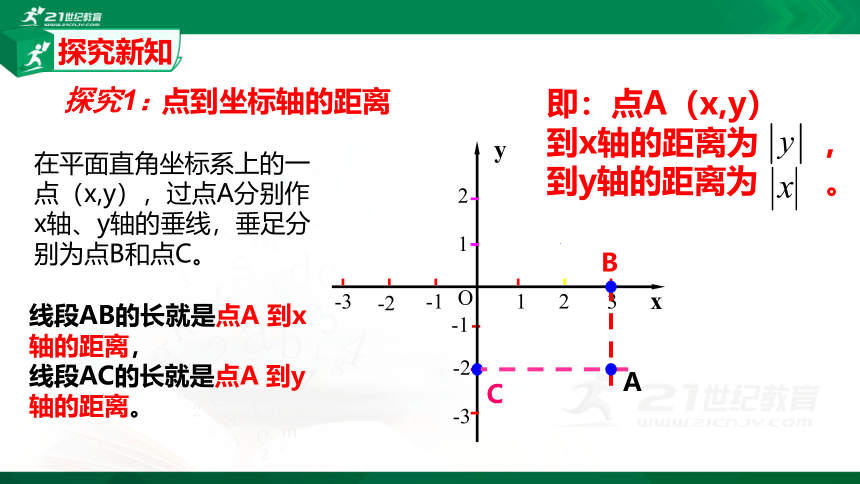
点到坐标轴的距离
在平面直角坐标系上的一点(x,y),过点A分别作x轴、y轴的垂线,垂足分别为点B和点C。
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
B
C
A
即:点A(x,y)
到x轴的距离为 ,到y轴的距离为 。
线段AB的长就是点A 到x轴的距离,
线段AC的长就是点A 到y轴的距离。
探究1:
探究新知
y
A
B
C
12
O
(1,4)
(-4,0)
(2,0)
2.已A(1,4),B(4,0),C(2,0)△ABC的面积是______。
1.点 M(- 8,12)到 x轴的距离是( ),到 y轴的距离是( )
8
12
例题讲解
(3,2)
(3,-2)
-2
-1
4
3
2
1
-3
-4
-4
y
1
2
3
-3
-1
-2
(-3,2)
(-3,-2)
0
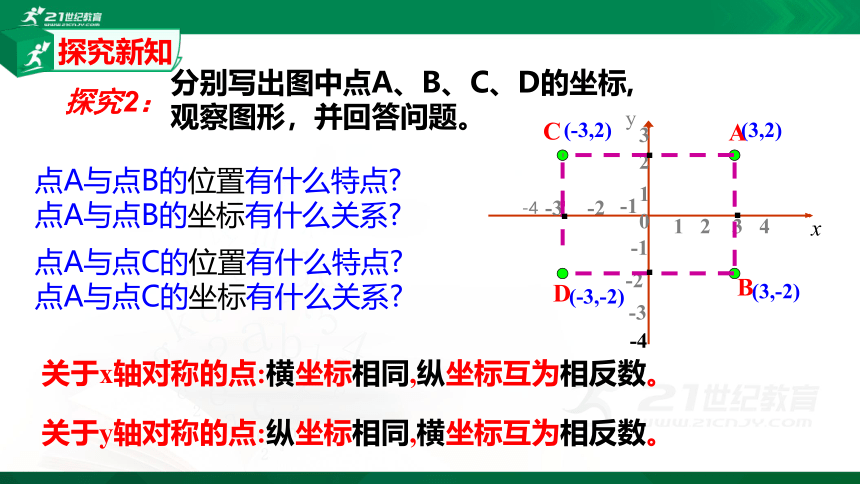
点A与点B的位置有什么特点?
点A与点B的坐标有什么关系?
点A与点C的位置有什么特点?
点A与点C的坐标有什么关系?
关于x轴对称的点:横坐标相同,纵坐标互为相反数。
关于y轴对称的点:纵坐标相同,横坐标互为相反数。
A
B
C
D
分别写出图中点A、B、C、D的坐标,
观察图形,并回答问题。
.
.
.
.
探究2:
探究新知
(3,2)
(3,-2)
-2
-1
4
3
2
1
-3
-4
-4
y
1
2
3
-3
-1
-2
(-3,2)
(-3,-2)
0
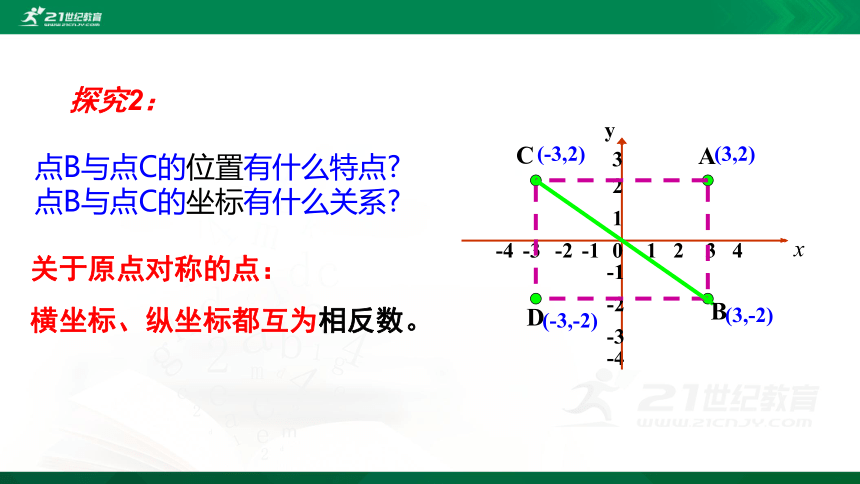
点B与点C的位置有什么特点?
点B与点C的坐标有什么关系?
关于原点对称的点:
横坐标、纵坐标都互为相反数。
A
B
C
D
探究2:
平面直角坐标系中的点p(x,y):
关于x轴的对称点是(x,-y);
关于y轴的对称点是(-x,y);
关于原点的对称点是(-x,-y)。
例:点(4,3)与点(4,- 3)的关系是( )
(A)关于原点对称
(B)关于 x轴对称
(C)关于 y轴对称
(D)不能构成对称关系
B
例题讲解
1.与点P(m,-1)关于原点的对称点是Q(2,n),
则m+n的值为_______。
2.若点A(n,2)与B(-3,m)关于原点对称,
则n-m的值为______。
-1
5
针对练习
2.点A在x轴上,距离原点4个单位长度,则A点的坐标是 _______________。
(4,0)或(-4,0)
3.若点P在第三象限且到x轴的距离为 2 ,
到y轴的距离为1.5,则点P的坐标是___________。
(-1.5,-2)
1.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( )
(A)平行于x轴 (B)平行于y轴
(C)经过原点 (D)以上都不对
B
课堂练习
3.若点P在第三象限且到x轴的距离为 2 ,
到y轴的距离为1.5,则点P的坐标是___________。
(-1.5,-2)
4.点P到x轴、y轴的距离分别是2、1,则点P的
坐标可能为 。
(1,2)、(1,-2)、(-1,2)、(-1,-2)
6.若点(a,b-1)在第二象限,则a的取值范围是_____,b的取值范围________。
5.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 , 则点P的位置在____________。
第二或四象限
a<0
b>1
7.实数 x,y满足 (x-1)2+ |y| = 0,则点 P( x,y)在( ).
(A)原点 (B)x轴正半轴
(C)第一象限 (D)任意位置
B
点A(x,y)
到x轴的距离为 ,到y轴的距离为 。
关于x轴对称的点:横坐标相同,纵坐标互为相反数。
关于y轴对称的点:纵坐标相同,横坐标互为相反数。
课堂小结
谢谢聆听
2021年春人教版七年级数学下册
第七章 平面直角坐标系
1,如何求点到坐标轴的距离?
2,关于坐标轴对称的点的坐标特征。
学习目标
2.已知P点坐标为(a+1,a-3)
①点P在x轴上,则a = ;
②点P在y轴上,则a = ;
3.若点P(x,y)在第四象限,|x|=5,|y|=4,则P点的坐标为__________。
3
(5,-4)
-1
1.已知a
变式:若点P(x,y)中,|x|=5,|y|=4,则P点的坐标为_______________________________________________。
(5,4)或(5,-4)或(-5,4)或(-5,-4)
复习巩固
点到坐标轴的距离
在平面直角坐标系上的一点(x,y),过点A分别作x轴、y轴的垂线,垂足分别为点B和点C。
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
B
C
A
即:点A(x,y)
到x轴的距离为 ,到y轴的距离为 。
线段AB的长就是点A 到x轴的距离,
线段AC的长就是点A 到y轴的距离。
探究1:
探究新知
y
A
B
C
12
O
(1,4)
(-4,0)
(2,0)
2.已A(1,4),B(4,0),C(2,0)△ABC的面积是______。
1.点 M(- 8,12)到 x轴的距离是( ),到 y轴的距离是( )
8
12
例题讲解
(3,2)
(3,-2)
-2
-1
4
3
2
1
-3
-4
-4
y
1
2
3
-3
-1
-2
(-3,2)
(-3,-2)
0
点A与点B的位置有什么特点?
点A与点B的坐标有什么关系?
点A与点C的位置有什么特点?
点A与点C的坐标有什么关系?
关于x轴对称的点:横坐标相同,纵坐标互为相反数。
关于y轴对称的点:纵坐标相同,横坐标互为相反数。
A
B
C
D
分别写出图中点A、B、C、D的坐标,
观察图形,并回答问题。
.
.
.
.
探究2:
探究新知
(3,2)
(3,-2)
-2
-1
4
3
2
1
-3
-4
-4
y
1
2
3
-3
-1
-2
(-3,2)
(-3,-2)
0
点B与点C的位置有什么特点?
点B与点C的坐标有什么关系?
关于原点对称的点:
横坐标、纵坐标都互为相反数。
A
B
C
D
探究2:
平面直角坐标系中的点p(x,y):
关于x轴的对称点是(x,-y);
关于y轴的对称点是(-x,y);
关于原点的对称点是(-x,-y)。
例:点(4,3)与点(4,- 3)的关系是( )
(A)关于原点对称
(B)关于 x轴对称
(C)关于 y轴对称
(D)不能构成对称关系
B
例题讲解
1.与点P(m,-1)关于原点的对称点是Q(2,n),
则m+n的值为_______。
2.若点A(n,2)与B(-3,m)关于原点对称,
则n-m的值为______。
-1
5
针对练习
2.点A在x轴上,距离原点4个单位长度,则A点的坐标是 _______________。
(4,0)或(-4,0)
3.若点P在第三象限且到x轴的距离为 2 ,
到y轴的距离为1.5,则点P的坐标是___________。
(-1.5,-2)
1.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( )
(A)平行于x轴 (B)平行于y轴
(C)经过原点 (D)以上都不对
B
课堂练习
3.若点P在第三象限且到x轴的距离为 2 ,
到y轴的距离为1.5,则点P的坐标是___________。
(-1.5,-2)
4.点P到x轴、y轴的距离分别是2、1,则点P的
坐标可能为 。
(1,2)、(1,-2)、(-1,2)、(-1,-2)
6.若点(a,b-1)在第二象限,则a的取值范围是_____,b的取值范围________。
5.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 , 则点P的位置在____________。
第二或四象限
a<0
b>1
7.实数 x,y满足 (x-1)2+ |y| = 0,则点 P( x,y)在( ).
(A)原点 (B)x轴正半轴
(C)第一象限 (D)任意位置
B
点A(x,y)
到x轴的距离为 ,到y轴的距离为 。
关于x轴对称的点:横坐标相同,纵坐标互为相反数。
关于y轴对称的点:纵坐标相同,横坐标互为相反数。
课堂小结
谢谢聆听
