5.5多边形和圆的初步认识 课件(共19张PPT)
文档属性
| 名称 | 5.5多边形和圆的初步认识 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 16:57:33 | ||
图片预览




文档简介
第五章 基本平面图形
5 多边形和圆的初步认识
知识点一 多边形及相关概念
多边形
由若干条不在同一直线上的线段首尾顺次相连组成的封闭平面图形叫做多边形,如三角形、四边形、五边形等,三角形是最简单的多边形
多边形
的边
组成多边形的线段
多边形
的内角
相邻两边组成的角
多边形的对角线
连接不相邻的两个顶点的线段
要点解读
(1)多边形的边数、顶点数及角的个数相等;
(2)没有特别说明,所说的多边形是指凸多边形;
(3)多边形用表示它的各个顶点的字母表示,表示多边形的字母要按顶点的顺序书写,可以按顺时针顺序,也可以按逆时针顺序;
(4)从n边形的一个顶点出发,可以引(n-3)条对角线,将n边形分成(n-2)个三角形,n边形的对角线条数是 .
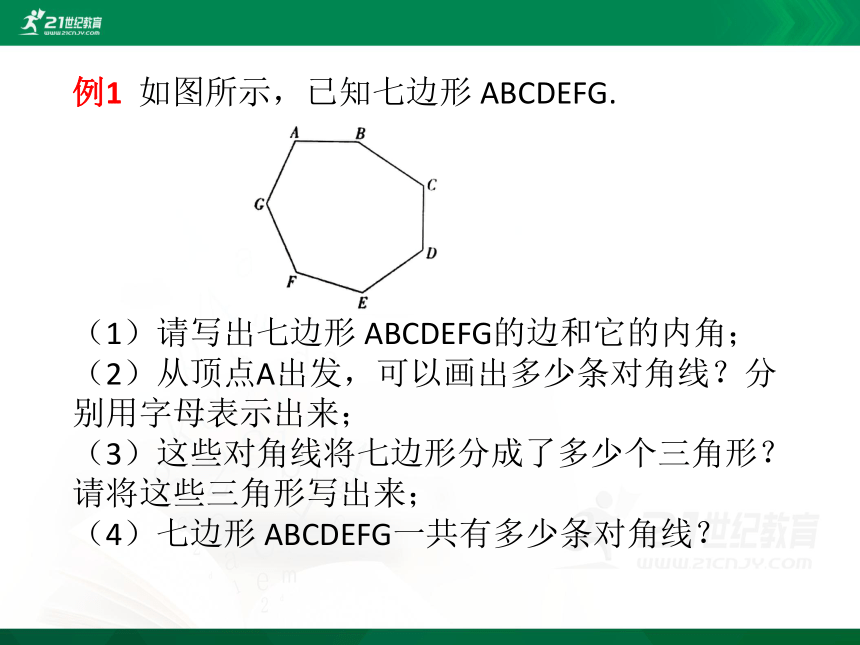
例1 如图所示,已知七边形 ABCDEFG.
(1)请写出七边形 ABCDEFG的边和它的内角;
(2)从顶点A出发,可以画出多少条对角线?分别用字母表示出来;
(3)这些对角线将七边形分成了多少个三角形?请将这些三角形写出来;
(4)七边形 ABCDEFG一共有多少条对角线?
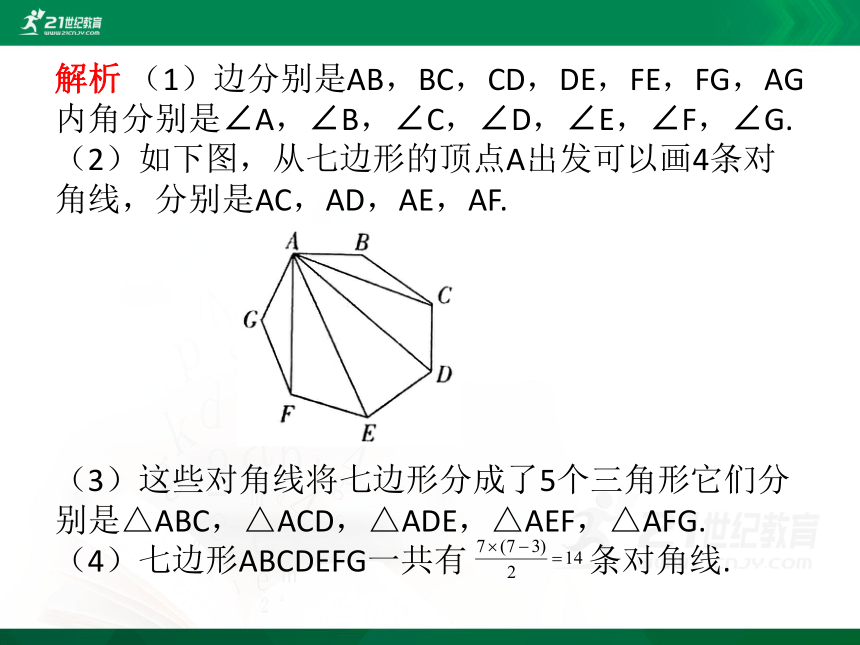
解析 (1)边分别是AB,BC,CD,DE,FE,FG,AG内角分别是∠A,∠B,∠C,∠D,∠E,∠F,∠G.
(2)如下图,从七边形的顶点A出发可以画4条对角线,分别是AC,AD,AE,AF.
(3)这些对角线将七边形分成了5个三角形它们分别是△ABC,△ACD,△ADE,△AEF,△AFG.
(4)七边形ABCDEFG一共有 条对角线.
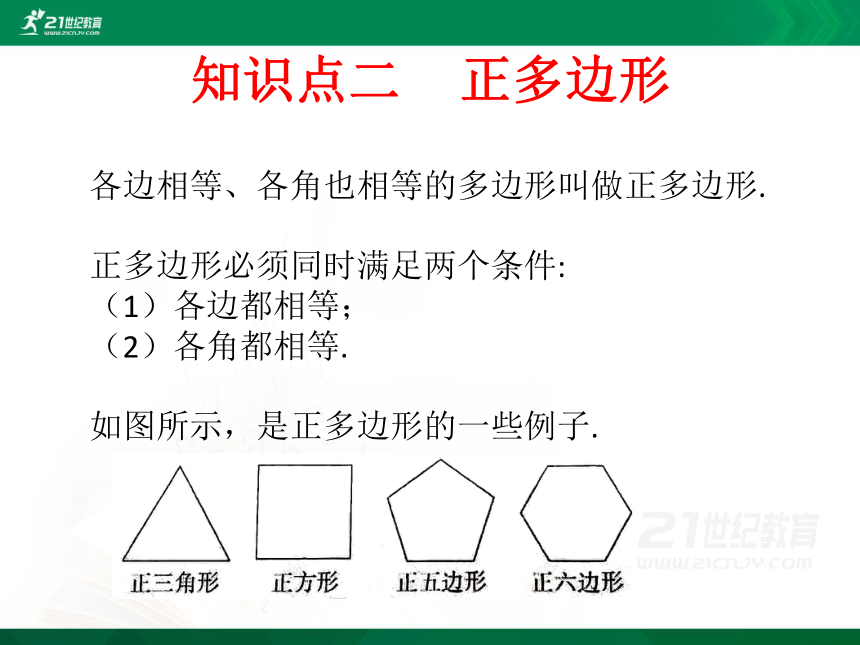
知识点二 正多边形
各边相等、各角也相等的多边形叫做正多边形.
正多边形必须同时满足两个条件:
(1)各边都相等;
(2)各角都相等.
如图所示,是正多边形的一些例子.
例2 下列说法错误的是( )
A.正多边形的各条边都相等
B.正多边形的各个角都相等
C.各个角都相等的多边形不一定是正多边形
D.各条边都相等的多边形一定是正多边形
例2 下列说法错误的是( )
A.正多边形的各条边都相等
B.正多边形的各个角都相等
C.各个角都相等的多边形不一定是正多边形
D.各条边都相等的多边形一定是正多边形
解析 正多边形必须同时满足两个条件:(1)各边都相等;(2)各个角都相等.故D错误.故选D.
答案 D
知识点三 圆及相关概念
1.圆:平面上,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫做圆.固定的端点O称为圆心,线段OA称为半径(如图所示).
温馨提示:①由圆的定义可知,确定圆有两个条件:一个是圆心,确定圆的位置;另一个是半径,确定圆的大小,两者缺一不可;②根据圆的定义可以知道“圆”指的是“圆周”,即那条封闭的曲线,而不是圆面.
2.弧: 圆上任意两点A,B间的部分叫做圆弧,简称弧,记作AB,读作“圆弧AB”或“弧AB”(如图所示)
3.扇形:由一条弧AB和经过这条弧的端点的两条半径OAOB所组成的图形叫做扇形(如上图所示).
4.圆心角:顶点在圆心的角叫做圆心角(如图所示)
例3 如图所示,王老师把班里同学的“上学方式”用一个圆来表示公交车、步行、其他三部分的占比为6:3:1.求这三个扇形的圆心角的度数步行.
例3 如图所示,王老师把班里同学的“上学方式”用一个圆来表示公交车、步行、其他三部分的占比为6:3:1.求这三个扇形的圆心角的度数步行.
解析 因为一个周角为360°,所以分成的三个扇形的圆心角分别是360°× =216°;
360°× =108°;360°× =36°.
经典例题
题型一 求多边形的边数问题
例1 从一个n边形的一个顶点出发引对角线,若所引对角线把这个多边形分割成了5个三角形,则n的值为( )
A.6 B.7 C.8 D.9
经典例题
题型一 求多边形的边数问题
例1 从一个n边形的一个顶点出发引对角线,若所引对角线把这个多边形分割成了5个三角形,则n的值为( )
A.6 B.7 C.8 D.9
解析 因为从n边形的一个顶点出发,可以引(n-3)条对角线,将n边形分成(n-2)个三角形,所以n-2=5,所以n=7.
答案 B
题型二 求扇形的面积
例2 已知一个扇形的圆心角的度数为45°,扇形所在圆的半径为3cm,求这个扇形的面积.
题型二 求扇形的面积
例2 已知一个扇形的圆心角的度数为45°,扇形所在圆的半径为3cm,求这个扇形的面积.
分析 由圆心角的度数确定扇形面积是圆面积的几分之几,再由圆面积求扇形面积.
题型二 求扇形的面积
例2 已知一个扇形的圆心角的度数为45°,扇形所在圆的半径为3cm,求这个扇形的面积.
分析 由圆心角的度数确定扇形面积是圆面积的几分之几,再由圆面积求扇形面积.
解析 由已知得圆的面积为π×32=9π(cm2),所以扇形的面积为9π× = π (cm2).
方法归纳 已知扇形的圆心角的度数为n°,扇形所在圆的面积为S,则扇形的面积为 .
题型三 已知圆的半径和扇形的面积,求扇形的圆心角
例3 已知在半径为2的圆中,有一个扇形的面积为π,则这个扇形的圆心角是多少度?
题型三 已知圆的半径和扇形的面积,求扇形的圆心角
例3 已知在半径为2的圆中,有一个扇形的面积为π,则这个扇形的圆心角是多少度?
解析 由已知得圆的面积为π×22=4π,又扇形的面积为π,所以扇形的圆心角是 .
5 多边形和圆的初步认识
知识点一 多边形及相关概念
多边形
由若干条不在同一直线上的线段首尾顺次相连组成的封闭平面图形叫做多边形,如三角形、四边形、五边形等,三角形是最简单的多边形
多边形
的边
组成多边形的线段
多边形
的内角
相邻两边组成的角
多边形的对角线
连接不相邻的两个顶点的线段
要点解读
(1)多边形的边数、顶点数及角的个数相等;
(2)没有特别说明,所说的多边形是指凸多边形;
(3)多边形用表示它的各个顶点的字母表示,表示多边形的字母要按顶点的顺序书写,可以按顺时针顺序,也可以按逆时针顺序;
(4)从n边形的一个顶点出发,可以引(n-3)条对角线,将n边形分成(n-2)个三角形,n边形的对角线条数是 .
例1 如图所示,已知七边形 ABCDEFG.
(1)请写出七边形 ABCDEFG的边和它的内角;
(2)从顶点A出发,可以画出多少条对角线?分别用字母表示出来;
(3)这些对角线将七边形分成了多少个三角形?请将这些三角形写出来;
(4)七边形 ABCDEFG一共有多少条对角线?
解析 (1)边分别是AB,BC,CD,DE,FE,FG,AG内角分别是∠A,∠B,∠C,∠D,∠E,∠F,∠G.
(2)如下图,从七边形的顶点A出发可以画4条对角线,分别是AC,AD,AE,AF.
(3)这些对角线将七边形分成了5个三角形它们分别是△ABC,△ACD,△ADE,△AEF,△AFG.
(4)七边形ABCDEFG一共有 条对角线.
知识点二 正多边形
各边相等、各角也相等的多边形叫做正多边形.
正多边形必须同时满足两个条件:
(1)各边都相等;
(2)各角都相等.
如图所示,是正多边形的一些例子.
例2 下列说法错误的是( )
A.正多边形的各条边都相等
B.正多边形的各个角都相等
C.各个角都相等的多边形不一定是正多边形
D.各条边都相等的多边形一定是正多边形
例2 下列说法错误的是( )
A.正多边形的各条边都相等
B.正多边形的各个角都相等
C.各个角都相等的多边形不一定是正多边形
D.各条边都相等的多边形一定是正多边形
解析 正多边形必须同时满足两个条件:(1)各边都相等;(2)各个角都相等.故D错误.故选D.
答案 D
知识点三 圆及相关概念
1.圆:平面上,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫做圆.固定的端点O称为圆心,线段OA称为半径(如图所示).
温馨提示:①由圆的定义可知,确定圆有两个条件:一个是圆心,确定圆的位置;另一个是半径,确定圆的大小,两者缺一不可;②根据圆的定义可以知道“圆”指的是“圆周”,即那条封闭的曲线,而不是圆面.
2.弧: 圆上任意两点A,B间的部分叫做圆弧,简称弧,记作AB,读作“圆弧AB”或“弧AB”(如图所示)
3.扇形:由一条弧AB和经过这条弧的端点的两条半径OAOB所组成的图形叫做扇形(如上图所示).
4.圆心角:顶点在圆心的角叫做圆心角(如图所示)
例3 如图所示,王老师把班里同学的“上学方式”用一个圆来表示公交车、步行、其他三部分的占比为6:3:1.求这三个扇形的圆心角的度数步行.
例3 如图所示,王老师把班里同学的“上学方式”用一个圆来表示公交车、步行、其他三部分的占比为6:3:1.求这三个扇形的圆心角的度数步行.
解析 因为一个周角为360°,所以分成的三个扇形的圆心角分别是360°× =216°;
360°× =108°;360°× =36°.
经典例题
题型一 求多边形的边数问题
例1 从一个n边形的一个顶点出发引对角线,若所引对角线把这个多边形分割成了5个三角形,则n的值为( )
A.6 B.7 C.8 D.9
经典例题
题型一 求多边形的边数问题
例1 从一个n边形的一个顶点出发引对角线,若所引对角线把这个多边形分割成了5个三角形,则n的值为( )
A.6 B.7 C.8 D.9
解析 因为从n边形的一个顶点出发,可以引(n-3)条对角线,将n边形分成(n-2)个三角形,所以n-2=5,所以n=7.
答案 B
题型二 求扇形的面积
例2 已知一个扇形的圆心角的度数为45°,扇形所在圆的半径为3cm,求这个扇形的面积.
题型二 求扇形的面积
例2 已知一个扇形的圆心角的度数为45°,扇形所在圆的半径为3cm,求这个扇形的面积.
分析 由圆心角的度数确定扇形面积是圆面积的几分之几,再由圆面积求扇形面积.
题型二 求扇形的面积
例2 已知一个扇形的圆心角的度数为45°,扇形所在圆的半径为3cm,求这个扇形的面积.
分析 由圆心角的度数确定扇形面积是圆面积的几分之几,再由圆面积求扇形面积.
解析 由已知得圆的面积为π×32=9π(cm2),所以扇形的面积为9π× = π (cm2).
方法归纳 已知扇形的圆心角的度数为n°,扇形所在圆的面积为S,则扇形的面积为 .
题型三 已知圆的半径和扇形的面积,求扇形的圆心角
例3 已知在半径为2的圆中,有一个扇形的面积为π,则这个扇形的圆心角是多少度?
题型三 已知圆的半径和扇形的面积,求扇形的圆心角
例3 已知在半径为2的圆中,有一个扇形的面积为π,则这个扇形的圆心角是多少度?
解析 由已知得圆的面积为π×22=4π,又扇形的面积为π,所以扇形的圆心角是 .
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
