北师大版八年级下册数学 1.2利用等腰直角三角形的性质求角度 练习(Word版 含解析)
文档属性
| 名称 | 北师大版八年级下册数学 1.2利用等腰直角三角形的性质求角度 练习(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 175.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-08 19:19:41 | ||
图片预览


文档简介
利用等腰直角三角形的性质求角度
一、选择题
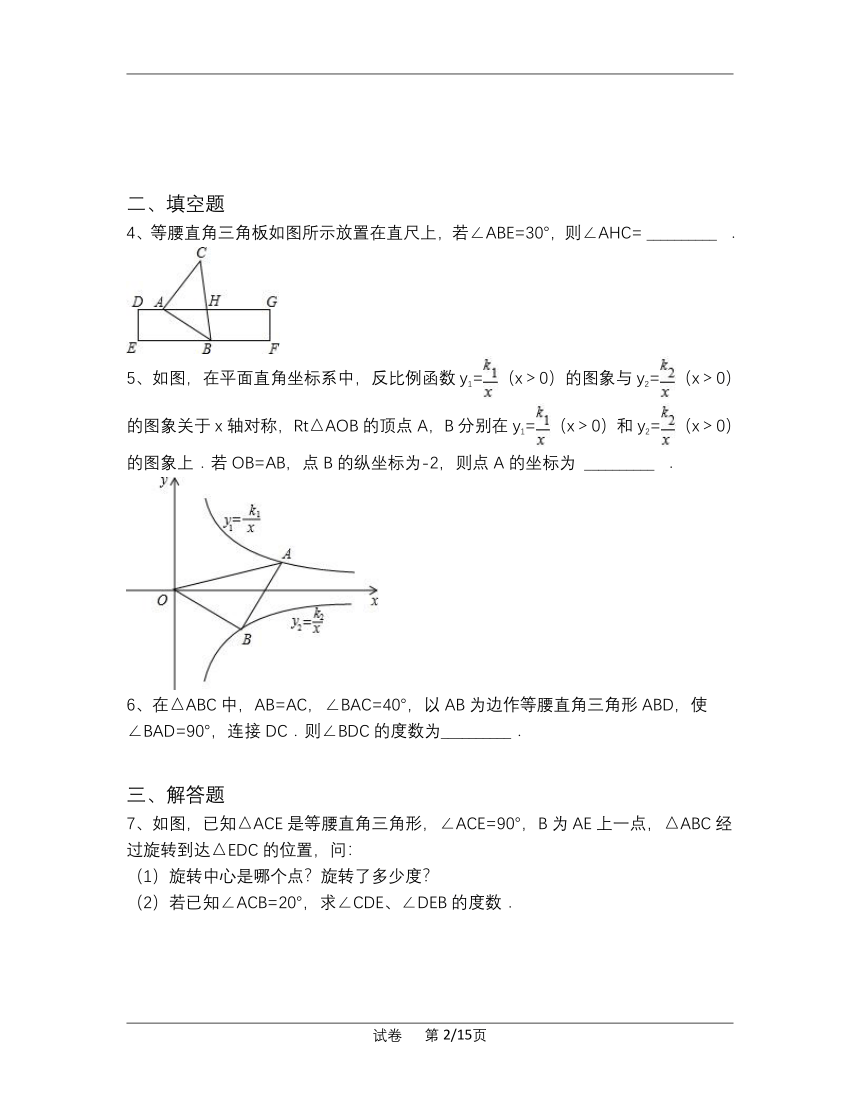
1、如图,Rt△ABC和Rt△DCE的斜边长相等,其中∠ACB=∠CED=90°,∠A=45°,∠CDE=30°,∠BCE=15°,连接DB,则∠EDB的度数为( )
A.10°
B.20°
C.7.5°
D.15°
2、如图,直线l∥m,△ABC是等腰直角三角形,若∠1=25°,则∠2的度数为( )
A.20°
B.25°
C.30°
D.35°
3、如图,在Rt△ABC中,AB=AC,AD⊥BC,垂足为D.E、F分别是CD、AD上的点,且CE=AF.如果∠AED=62°,那么∠DBF=( )
A.62°
B.38°
C.28°
D.26°
二、填空题
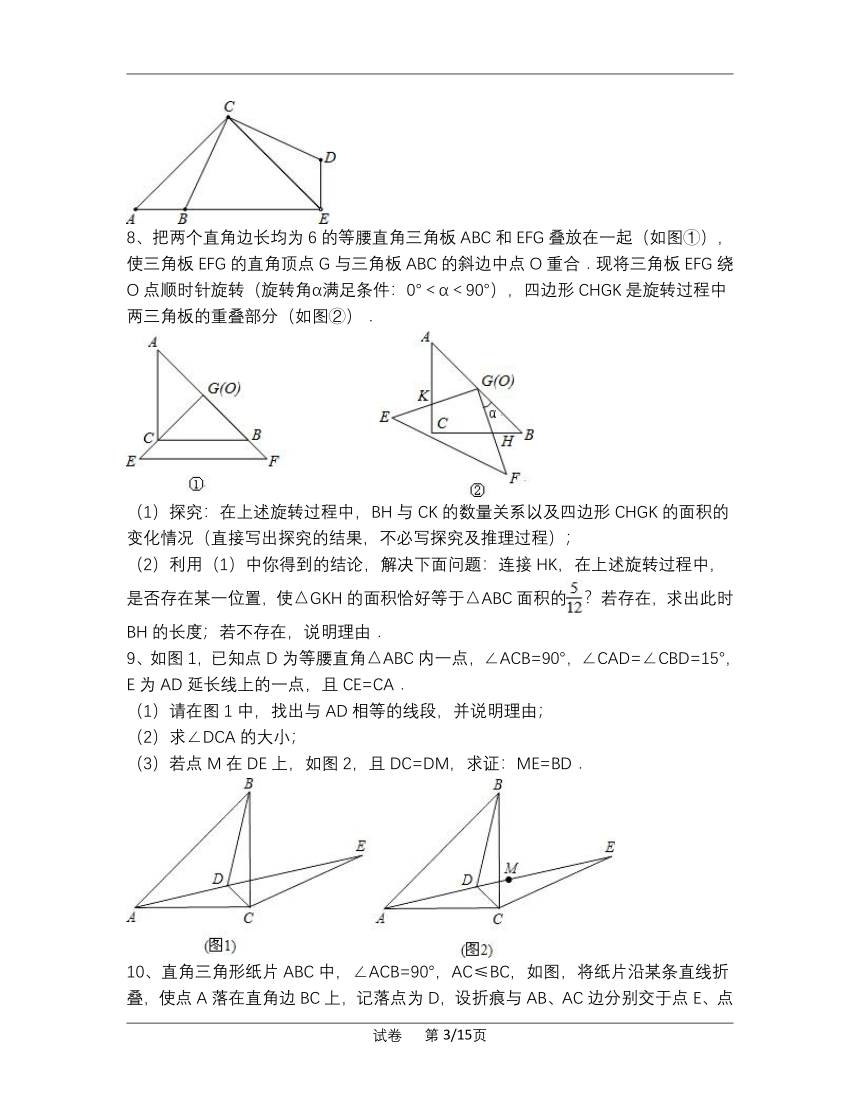
4、等腰直角三角板如图所示放置在直尺上,若∠ABE=30°,则∠AHC=
__________
.
5、如图,在平面直角坐标系中,反比例函数y1=(x>0)的图象与y2=(x>0)的图象关于x轴对称,Rt△AOB的顶点A,B分别在y1=(x>0)和y2=(x>0)的图象上.若OB=AB,点B的纵坐标为-2,则点A的坐标为
__________
.
6、在△ABC中,AB=AC,∠BAC=40°,以AB为边作等腰直角三角形ABD,使∠BAD=90°,连接DC.则∠BDC的度数为__________.
三、解答题
7、如图,已知△ACE是等腰直角三角形,∠ACE=90°,B为AE上一点,△ABC经过旋转到达△EDC的位置,问:
(1)旋转中心是哪个点?旋转了多少度?
(2)若已知∠ACB=20°,求∠CDE、∠DEB的度数.
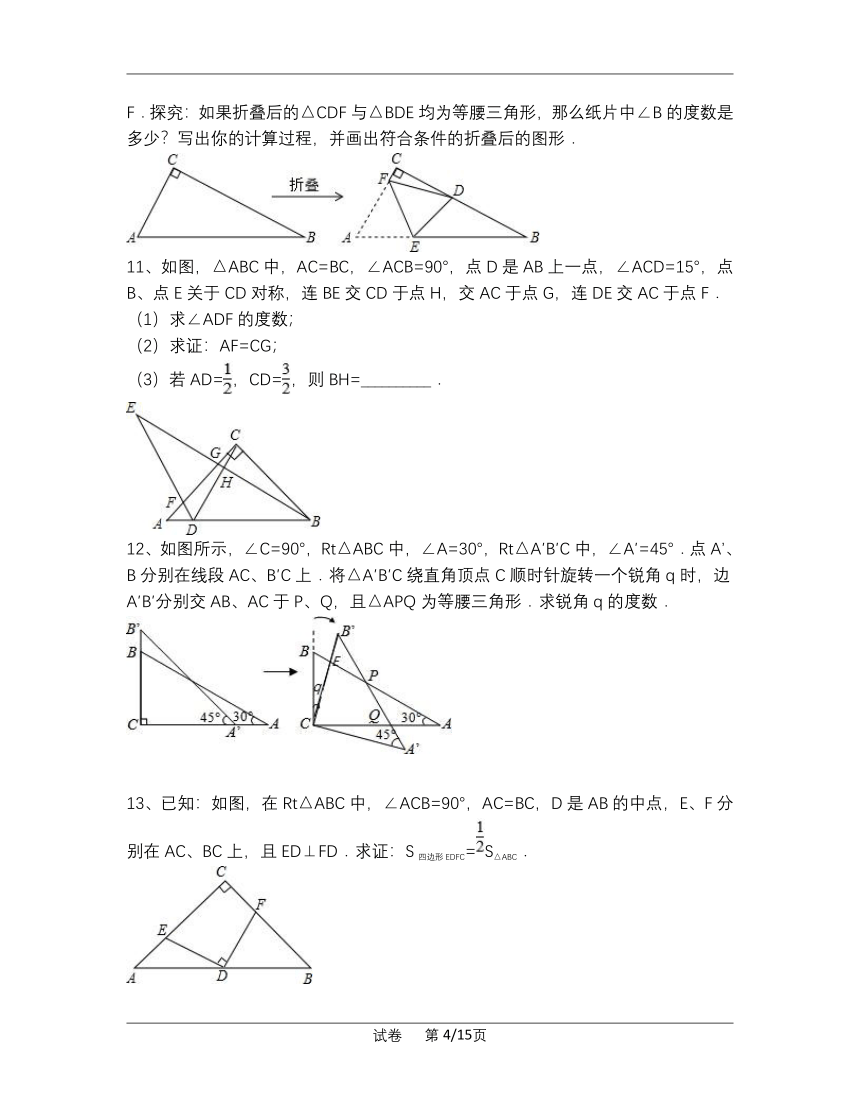
8、把两个直角边长均为6的等腰直角三角板ABC和EFG叠放在一起(如图①),使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点顺时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).
(1)探究:在上述旋转过程中,BH与CK的数量关系以及四边形CHGK的面积的变化情况(直接写出探究的结果,不必写探究及推理过程);
(2)利用(1)中你得到的结论,解决下面问题:连接HK,在上述旋转过程中,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的?若存在,求出此时BH的长度;若不存在,说明理由.
9、如图1,已知点D为等腰直角△ABC内一点,∠ACB=90°,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
(1)请在图1中,找出与AD相等的线段,并说明理由;
(2)求∠DCA的大小;
(3)若点M在DE上,如图2,且DC=DM,求证:ME=BD.
10、直角三角形纸片ABC中,∠ACB=90°,AC≤BC,如图,将纸片沿某条直线折叠,使点A落在直角边BC上,记落点为D,设折痕与AB、AC边分别交于点E、点F.探究:如果折叠后的△CDF与△BDE均为等腰三角形,那么纸片中∠B的度数是多少?写出你的计算过程,并画出符合条件的折叠后的图形.
11、如图,△ABC中,AC=BC,∠ACB=90°,点D是AB上一点,∠ACD=15°,点B、点E关于CD对称,连BE交CD于点H,交AC于点G,连DE交AC于点F.
(1)求∠ADF的度数;
(2)求证:AF=CG;
(3)若AD=,CD=,则BH=__________.
12、如图所示,∠C=90°,Rt△ABC中,∠A=30°,Rt△A′B′C中,∠A′=45°.点A’、B分别在线段AC、B′C上.将△A′B′C绕直角顶点C顺时针旋转一个锐角q时,边A′B′分别交AB、AC于P、Q,且△APQ为等腰三角形.求锐角q的度数.
13、已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,D是AB的中点,E、F分别在AC、BC上,且ED⊥FD.求证:S四边形EDFC=S△ABC.
试卷
第6/16页
利用等腰直角三角形的性质求角度的答案和解析
一、选择题
1、答案:
D
试题分析:设AB、CD相交于点F,根据直角三角形两锐角互余求出∠BCD=45°,再根据等腰直角三角形的性质可得CF=BF=AB,CF⊥AB,再求出DF=BF,然后根据等腰三角形两底角相等列式计算即可求出∠FDB,然后由∠EDB=∠FDB-∠CDE即可求出∠EDB的度数.
试题解析:如图,设AB、CD相交于点F,
∵∠CED=90°,∠CDE=30°,∠BCE=15°,
∴∠BCD=90°-30°-15°=45°,
∵∠ACB=90°,∠A=45°,
∴△ABC是等腰直角三角形,
∴CF=BF=AB,CF⊥AB,
∵AB=CD,
∴DF=BF=AB,
∴∠BDF=(180°-90°)=45°,
∴∠BDE=∠BDF-∠CDE=45°-30°=15°.
故选D.
2、答案:
A
试题分析:首先根据等腰直角三角形的性质可得∠A=45°,再根据平行线的性质可得∠3=∠4=115°,然后根据三角形内角和可得∠5的度数,再根据对顶角相等可得答案.
试题解析:∵△ABC是等腰直角三角形,
∴∠A=45°,
∵∠1=25°,∠ACB=90°,
∴∠3=90°+25°=115°,
∵l∥m,
∴∠3=∠4=115°,
∴∠5=180°-115°-45°=20°,
∴∠2=∠3=20°,
故选:A.
3、答案:
C
试题分析:主要考查:等腰三角形的三线合一,直角三角形的性质.注意:根据斜边和直角边对应相等可以证明△BDF≌△ADE.
试题解析:∵AB=AC,AD⊥BC,
∴BD=CD.
又∵∠BAC=90°,
∴BD=AD=CD.
又∵CE=AF,
∴DF=DE.
∴Rt△BDF≌Rt△ADE(SAS).
∴∠DBF=∠DAE=90°-62°=28°.
故选C.
二、填空题
4、答案:
试题分析:先根据△ABC是等腰直角三角形得出∠ABC=45°,再由∠ABE=30°可求出∠CBE的度数,根据平行线的性质即可得出结论.
试题解析:∵△ABC是等腰直角三角形,
∴∠ABC=45°.
∵∠ABE=30°,
∴∠CBE=45°+30°=75°.
∵直尺的两边互相平行,
∴∠AHC=∠CBE=75°.
故答案为:75°.
5、答案:
试题分析:利用等腰直角三角形的性质结合全等三角形的判定方法得出△OEB≌△BFA(AAS),由反比例函数y1=(x>0)的图象与y2=(x>0)的图象关于x轴对称,进而得出k1+k2=0,表示出A,B点坐标列方程即可求出结论.
试题解析:过点B作x轴的平行线EB,过点A作AF⊥EB的延长线于点F,
∵等腰Rt△OAB,∠OBA=90°,
∴∠OBE+∠ABF=90°,∠ABF+∠BAF=90°,
∴∠OBE=∠BAF,
在△OEB和△BFA中,
,
∴△OEB≌△BFA(AAS),
∴EO=BF,BE=AF=2,
∵设AD=y,则OE=BF=2-y,EF=2-y+2=4-y,
故A(4-y,y),B(2,y-2),
∵反比例函数y1=(x>0)的图象与反比例函数y2=(x>0)的图象关于x轴对称,
∴k1+k2=0,
即(4-y)y+2(y-2)=0,
解得:y1=3+(不合题意舍去),y2=3-,
则点A的纵坐标为:3-,
∵EF=4-y=1+,
∴A(1+,3-).
故答案为:(1+,3-).
6、答案:
试题分析:根据题意,画出示意图,如图①,所示,根据AB=AD,∠BAD=90°求出∠BDA=45°,然后根据等腰三角形的性质和三角形内角和定理即可求出∠BDC的度数.同理可求图②∠BDC的度数.
试题解析:根据题意,画出示意图,有两种情况:如图①,图②所示,
在图①中,∵AB=AD,∠BAD=90°,
∴∠BDA=45°,
∵∠BDC=45°-∠ADC,AD=AC=AB,
∴△ADC为等腰三角形.
∴∠BDC=45°-[180°-(40°+90°)]÷2=20°;
在图②中,∠BDC=∠ADC-45°
=[180°-(90°-40°)]÷2-45°=20°.
故答案为20°.
三、解答题
7、答案:
试题分析:(1)根据旋转中心的定义以及旋转角的定义解答即可;
(2)由旋转的性质可知:∠CDE=∠ABC由此可得∠CDE的度数,再根据∠DEB=∠CED+∠CEB计算即可.
试题解析:(1)∵△ABC经过旋转到达△EDC的位置,
∴△ABC≌△EDC,
∴C是旋转中心,
∵AC=CE,
∴AC和CE之间的夹角为旋转角,
∵∠ACE=90°,
∴旋转了90度;
(2)∵△ACE是等腰直角三角形,∠ACE=90°,
∴∠A=∠CEB=45°,
∵∠ACB=20°,
∴∠ABC=180°-∠A-∠ACB=115°,
∴∠CDE=∠ABC=115°,
∵∠DEC=∠A=45°,
∴∠DEB=∠CED+∠CEB=90°.
8、答案:
试题分析:(1)先由ASA证出△CGK≌△BGH,再根据全等三角形的性质得出BH=CK,根据全等得出四边形CKGH的面积等于三角形ACB面积一半;
(2)根据面积公式得出S△GHK=S四边形CKGH-S△CKH=x2-3x+9,根据△GKH的面积恰好等于△ABC面积的,代入得出方程,求出即可.
试题解析:(1)BH与CK的数量关系:BH=CK,理由是:
连接OC,由直角三角形斜边上中线性质得出OC=BG,
∵AC=BC,O为AB中点,∠ACB=90°,
∴∠B=∠ACG=45°,CO⊥AB,
∴∠CGB=90°=∠KGH,
∴都减去∠CGH得:∠BGH=∠CGK,
在△CGK和△BGH中
∵,
∴△CGK≌△BGH(ASA),
∴CK=BH,即BH=CK;
四边形CHGK的面积的变化情况:四边形CHGK的面积不变,始终等于四边形CQGZ的面积,即等于△ACB面积的一半,等于9;
????????????????????????????????
(2)假设存在使△GKH的面积恰好等于△ABC面积的的位置.
设BH=x,由题意及(1)中结论可得,CK=BH=x,CH=CB-BH=6-x,
∴S△CHK=CH×CK=3x-x2,
∴S△GHK=S四边形CKGH-S△CKH=9-(3x-x2)=x2-3x+9,
∵△GKH的面积恰好等于△ABC面积的,
∴x2-3x+9=××6×6,
解得(经检验,均符合题意).????????????
∴存在使△GKH的面积恰好等于△ABC面积的的位置,此时x的值为.
9、答案:
试题分析:(1)根据条件可以得出∠DAB=DBA,从而可以得出AD=BD;
(2)根据等腰直角三角形的性质可以得出△ADC≌△BDC,就可以得出∠DCA=∠DCB,从而可以得出结论;
(3)连结MC,证明△DCM是等边三角形,就可以得出CM=CD,∠MCE=45°,通过证明△MCE≌△DCB就可以得出结论.
试题解析:(1)BD=AD,
理由:∵△ABC是等腰直角三角形,
∴∠BAC=∠ABC=45°.
∵∠CAD=∠CBD=15°
∴∠BAC-∠CAD=∠ABC-∠CBD=45°-15°=30°,
即∠DAB=∠DBA,
∴BD=AD;
(2)∵△ABC是等腰直角三角形,
∴AC=BC,∠ACB=90°,
∵在△ADC和△BDC中,
,
∴△ADC≌△BDC(SAS),
∴∠DCA=∠DCB,
∴∠DCA=∠ACB=×90°=45°;
(3)连结MC,
∵∠MDC=∠CAD+∠ACD,
∴∠MDC=15°+45°=60°.
∵DC=DM,
∴△DCM是等边三角形.
∴CD=CM=DM,∠CDM=∠DMC=∠DCM.
∵CE=CA,
∴∠CAE=∠CEA=15°,BC=CE,
∴∠ACE=150°
∴∠MCE=150°-45°-60°=45°,
∴∠MCE=∠DCB,
∵在△MCE和△DCB中,
,
∴△MCE≌△DCB(SAS),
∴ME=BD.
10、答案:
试题分析:先确定△CDF是等腰三角形,得出∠CFD=∠CDF=45°,因为不确定△BDE是以那两条边为腰的等腰三角形,故需讨论,①DE=DB,②BD=BE,③DE=BE,然后分别利用角的关系得出答案即可.
试题解析:∵△CDF中,∠C=90°,且△CDF是等腰三角形,
∴CF=CD,
∴∠CFD=∠CDF=45°,
设∠DAE=x°,由对称性可知,AF=FD,AE=DE,
∴∠FDA=∠CFD=22.5°,∠DEB=2x°,
分类如下:
①当DE=DB时,∠B=∠DEB=2x°,
由∠CDE=∠DEB+∠B,得45°+22.5°+x=4x,
解得:x=22.5°.此时∠B=2x=45°;
见图形(1),说明:图中AD应平分∠CAB.
②当BD=BE时,则∠B=(180°-4x)°,
由∠CDE=∠DEB+∠B得:45°+22.5°+x=2x+180°-4x,
解得x=37.5°,此时∠B=(180-4x)°=30°.
图形(2)说明:∠CAB=60°,∠CAD=22.5°.
③DE=BE时,则∠B=()°,
由∠CDE=∠DEB+∠B得,45°+22.5°+x=2x+,
此方程无解.
∴DE=BE不成立.
综上所述∠B=45°或30°.
11、答案:
试题分析:(1)求出∠CDB,根据轴对称得出∠EDC=∠CDB=60°,即可得出答案.
(2)过A作AM⊥AC交ED延长线于M,证△ADM≌△ADC,推出AC=AM=BC,证△AFM≌△CBG,即可推出答案.
(3)过A作AQ⊥CD交CD延长线于Q,求出DQ,求出CQ,证△AQC≌△CHB,推出BH=CQ即可.
试题解析:(1)∵∠ACB=90°,∠ACD=15°,
∴∠DCB=75°,
∵△ABC中,AC=BC,∠ACB=90°,
∴∠CAD=∠CBA=45°,
∴∠CDB=180°-45°-75°=60°,
∵点B、点E关于CD对称,
∴∠EDC=∠CDB=60°,
∴∠ADF=180°-60°-60°=60°;
(2)证明:过A作AM⊥AC交ED延长线于M,
则∠FAM=90°=∠BCG,∠MAD=90°-45°=45°=∠CAD,
∵∠MAD=45°,∠ADF=60°,
∴∠M=60°-45°=15°=∠ACD,
∵点B、点E关于CD对称,
∴CD⊥BE,
∴∠CHG=90°,
∵∠BCG=90°,
∴∠CBG+∠CGB=∠CGB+∠ACD=90°,
∴∠CBG=∠ACD=15°,
在△ACD和△AMD中,
,
∴△ACD≌△AMD(AAS),
∴AC=AM=BC,
在△FAM和△GCB中,
,
∴△FAM≌△GCB(ASA),
∴AF=CG;
(3)过A作AQ⊥CD交CD延长线于Q,
∵在△AQD中,∠Q=90°,∠QAD=90°-∠ADQ=90°-∠CDB=90°-60°=30°,AD=,
∴DQ=AD=,
∴CQ=+=,
在△AQC和△CHB中,
∴△AQC≌△CHB(AAS),
∴BH=CQ=.
故答案为:.
12、答案:
试题分析:由于△APQ为等腰三角形,∠A为底角或顶角不能确定,故应分∠A为底角和顶角两种情况进行讨论.
试题解析:①当∠A为等腰△AOQ的底角时,此时PQ=AQ,
∵∠A=30°,
∴∠AQP=∠A′QC=120°,
∵∠A′=45°,
∴∠A′CQ=180°-∠A′QC-∠A′=180°-120°-45°=15°,
由旋转的性质可知∠q=∠A′CQ=15°;
②当∠A为等腰△AOQ的顶角时,此时AP=AQ,
∵∠A=30°,
∴∠APQ=∠B′PQ===75°,
∵∠B′=90°-∠A=90°-30°=60°,
∴∠B′EP=∠BEC=180°-∠B′-∠B′PQ=180°-45°-75°=60°,
∵∠B=90°-∠A=90°-30°=60°,
∴∠q=180°-∠B-∠BEC=180°-60°-60°=60°.
故答案为:15°,60°.
13、答案:
试题分析:连接CD,由等腰直角三角形的性质用ASA证得△CFD≌△AED,△CED≌△BFD即可.
试题解析:证明:连接CD,
∵△ABC是等腰直角三角形,D是AB的中点,
∴CD=AD=BD,∠A=∠B=∠ACD=∠BCD=45°,CD⊥AB.
∵∠CDF+∠CDE=∠CDE+∠EDA=90°,
∴∠CDF=ADE.
∴△CDF≌△ADE.
同理△CED≌△BFD,
∴S△CDF=S△ADE,S△CED=S△BFD.
∴S四边形EDFC=S△ABC.
一、选择题
1、如图,Rt△ABC和Rt△DCE的斜边长相等,其中∠ACB=∠CED=90°,∠A=45°,∠CDE=30°,∠BCE=15°,连接DB,则∠EDB的度数为( )
A.10°
B.20°
C.7.5°
D.15°
2、如图,直线l∥m,△ABC是等腰直角三角形,若∠1=25°,则∠2的度数为( )
A.20°
B.25°
C.30°
D.35°
3、如图,在Rt△ABC中,AB=AC,AD⊥BC,垂足为D.E、F分别是CD、AD上的点,且CE=AF.如果∠AED=62°,那么∠DBF=( )
A.62°
B.38°
C.28°
D.26°
二、填空题
4、等腰直角三角板如图所示放置在直尺上,若∠ABE=30°,则∠AHC=
__________
.
5、如图,在平面直角坐标系中,反比例函数y1=(x>0)的图象与y2=(x>0)的图象关于x轴对称,Rt△AOB的顶点A,B分别在y1=(x>0)和y2=(x>0)的图象上.若OB=AB,点B的纵坐标为-2,则点A的坐标为
__________
.
6、在△ABC中,AB=AC,∠BAC=40°,以AB为边作等腰直角三角形ABD,使∠BAD=90°,连接DC.则∠BDC的度数为__________.
三、解答题
7、如图,已知△ACE是等腰直角三角形,∠ACE=90°,B为AE上一点,△ABC经过旋转到达△EDC的位置,问:
(1)旋转中心是哪个点?旋转了多少度?
(2)若已知∠ACB=20°,求∠CDE、∠DEB的度数.
8、把两个直角边长均为6的等腰直角三角板ABC和EFG叠放在一起(如图①),使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点顺时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).
(1)探究:在上述旋转过程中,BH与CK的数量关系以及四边形CHGK的面积的变化情况(直接写出探究的结果,不必写探究及推理过程);
(2)利用(1)中你得到的结论,解决下面问题:连接HK,在上述旋转过程中,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的?若存在,求出此时BH的长度;若不存在,说明理由.
9、如图1,已知点D为等腰直角△ABC内一点,∠ACB=90°,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
(1)请在图1中,找出与AD相等的线段,并说明理由;
(2)求∠DCA的大小;
(3)若点M在DE上,如图2,且DC=DM,求证:ME=BD.
10、直角三角形纸片ABC中,∠ACB=90°,AC≤BC,如图,将纸片沿某条直线折叠,使点A落在直角边BC上,记落点为D,设折痕与AB、AC边分别交于点E、点F.探究:如果折叠后的△CDF与△BDE均为等腰三角形,那么纸片中∠B的度数是多少?写出你的计算过程,并画出符合条件的折叠后的图形.
11、如图,△ABC中,AC=BC,∠ACB=90°,点D是AB上一点,∠ACD=15°,点B、点E关于CD对称,连BE交CD于点H,交AC于点G,连DE交AC于点F.
(1)求∠ADF的度数;
(2)求证:AF=CG;
(3)若AD=,CD=,则BH=__________.
12、如图所示,∠C=90°,Rt△ABC中,∠A=30°,Rt△A′B′C中,∠A′=45°.点A’、B分别在线段AC、B′C上.将△A′B′C绕直角顶点C顺时针旋转一个锐角q时,边A′B′分别交AB、AC于P、Q,且△APQ为等腰三角形.求锐角q的度数.
13、已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,D是AB的中点,E、F分别在AC、BC上,且ED⊥FD.求证:S四边形EDFC=S△ABC.
试卷
第6/16页
利用等腰直角三角形的性质求角度的答案和解析
一、选择题
1、答案:
D
试题分析:设AB、CD相交于点F,根据直角三角形两锐角互余求出∠BCD=45°,再根据等腰直角三角形的性质可得CF=BF=AB,CF⊥AB,再求出DF=BF,然后根据等腰三角形两底角相等列式计算即可求出∠FDB,然后由∠EDB=∠FDB-∠CDE即可求出∠EDB的度数.
试题解析:如图,设AB、CD相交于点F,
∵∠CED=90°,∠CDE=30°,∠BCE=15°,
∴∠BCD=90°-30°-15°=45°,
∵∠ACB=90°,∠A=45°,
∴△ABC是等腰直角三角形,
∴CF=BF=AB,CF⊥AB,
∵AB=CD,
∴DF=BF=AB,
∴∠BDF=(180°-90°)=45°,
∴∠BDE=∠BDF-∠CDE=45°-30°=15°.
故选D.
2、答案:
A
试题分析:首先根据等腰直角三角形的性质可得∠A=45°,再根据平行线的性质可得∠3=∠4=115°,然后根据三角形内角和可得∠5的度数,再根据对顶角相等可得答案.
试题解析:∵△ABC是等腰直角三角形,
∴∠A=45°,
∵∠1=25°,∠ACB=90°,
∴∠3=90°+25°=115°,
∵l∥m,
∴∠3=∠4=115°,
∴∠5=180°-115°-45°=20°,
∴∠2=∠3=20°,
故选:A.
3、答案:
C
试题分析:主要考查:等腰三角形的三线合一,直角三角形的性质.注意:根据斜边和直角边对应相等可以证明△BDF≌△ADE.
试题解析:∵AB=AC,AD⊥BC,
∴BD=CD.
又∵∠BAC=90°,
∴BD=AD=CD.
又∵CE=AF,
∴DF=DE.
∴Rt△BDF≌Rt△ADE(SAS).
∴∠DBF=∠DAE=90°-62°=28°.
故选C.
二、填空题
4、答案:
试题分析:先根据△ABC是等腰直角三角形得出∠ABC=45°,再由∠ABE=30°可求出∠CBE的度数,根据平行线的性质即可得出结论.
试题解析:∵△ABC是等腰直角三角形,
∴∠ABC=45°.
∵∠ABE=30°,
∴∠CBE=45°+30°=75°.
∵直尺的两边互相平行,
∴∠AHC=∠CBE=75°.
故答案为:75°.
5、答案:
试题分析:利用等腰直角三角形的性质结合全等三角形的判定方法得出△OEB≌△BFA(AAS),由反比例函数y1=(x>0)的图象与y2=(x>0)的图象关于x轴对称,进而得出k1+k2=0,表示出A,B点坐标列方程即可求出结论.
试题解析:过点B作x轴的平行线EB,过点A作AF⊥EB的延长线于点F,
∵等腰Rt△OAB,∠OBA=90°,
∴∠OBE+∠ABF=90°,∠ABF+∠BAF=90°,
∴∠OBE=∠BAF,
在△OEB和△BFA中,
,
∴△OEB≌△BFA(AAS),
∴EO=BF,BE=AF=2,
∵设AD=y,则OE=BF=2-y,EF=2-y+2=4-y,
故A(4-y,y),B(2,y-2),
∵反比例函数y1=(x>0)的图象与反比例函数y2=(x>0)的图象关于x轴对称,
∴k1+k2=0,
即(4-y)y+2(y-2)=0,
解得:y1=3+(不合题意舍去),y2=3-,
则点A的纵坐标为:3-,
∵EF=4-y=1+,
∴A(1+,3-).
故答案为:(1+,3-).
6、答案:
试题分析:根据题意,画出示意图,如图①,所示,根据AB=AD,∠BAD=90°求出∠BDA=45°,然后根据等腰三角形的性质和三角形内角和定理即可求出∠BDC的度数.同理可求图②∠BDC的度数.
试题解析:根据题意,画出示意图,有两种情况:如图①,图②所示,
在图①中,∵AB=AD,∠BAD=90°,
∴∠BDA=45°,
∵∠BDC=45°-∠ADC,AD=AC=AB,
∴△ADC为等腰三角形.
∴∠BDC=45°-[180°-(40°+90°)]÷2=20°;
在图②中,∠BDC=∠ADC-45°
=[180°-(90°-40°)]÷2-45°=20°.
故答案为20°.
三、解答题
7、答案:
试题分析:(1)根据旋转中心的定义以及旋转角的定义解答即可;
(2)由旋转的性质可知:∠CDE=∠ABC由此可得∠CDE的度数,再根据∠DEB=∠CED+∠CEB计算即可.
试题解析:(1)∵△ABC经过旋转到达△EDC的位置,
∴△ABC≌△EDC,
∴C是旋转中心,
∵AC=CE,
∴AC和CE之间的夹角为旋转角,
∵∠ACE=90°,
∴旋转了90度;
(2)∵△ACE是等腰直角三角形,∠ACE=90°,
∴∠A=∠CEB=45°,
∵∠ACB=20°,
∴∠ABC=180°-∠A-∠ACB=115°,
∴∠CDE=∠ABC=115°,
∵∠DEC=∠A=45°,
∴∠DEB=∠CED+∠CEB=90°.
8、答案:
试题分析:(1)先由ASA证出△CGK≌△BGH,再根据全等三角形的性质得出BH=CK,根据全等得出四边形CKGH的面积等于三角形ACB面积一半;
(2)根据面积公式得出S△GHK=S四边形CKGH-S△CKH=x2-3x+9,根据△GKH的面积恰好等于△ABC面积的,代入得出方程,求出即可.
试题解析:(1)BH与CK的数量关系:BH=CK,理由是:
连接OC,由直角三角形斜边上中线性质得出OC=BG,
∵AC=BC,O为AB中点,∠ACB=90°,
∴∠B=∠ACG=45°,CO⊥AB,
∴∠CGB=90°=∠KGH,
∴都减去∠CGH得:∠BGH=∠CGK,
在△CGK和△BGH中
∵,
∴△CGK≌△BGH(ASA),
∴CK=BH,即BH=CK;
四边形CHGK的面积的变化情况:四边形CHGK的面积不变,始终等于四边形CQGZ的面积,即等于△ACB面积的一半,等于9;
????????????????????????????????
(2)假设存在使△GKH的面积恰好等于△ABC面积的的位置.
设BH=x,由题意及(1)中结论可得,CK=BH=x,CH=CB-BH=6-x,
∴S△CHK=CH×CK=3x-x2,
∴S△GHK=S四边形CKGH-S△CKH=9-(3x-x2)=x2-3x+9,
∵△GKH的面积恰好等于△ABC面积的,
∴x2-3x+9=××6×6,
解得(经检验,均符合题意).????????????
∴存在使△GKH的面积恰好等于△ABC面积的的位置,此时x的值为.
9、答案:
试题分析:(1)根据条件可以得出∠DAB=DBA,从而可以得出AD=BD;
(2)根据等腰直角三角形的性质可以得出△ADC≌△BDC,就可以得出∠DCA=∠DCB,从而可以得出结论;
(3)连结MC,证明△DCM是等边三角形,就可以得出CM=CD,∠MCE=45°,通过证明△MCE≌△DCB就可以得出结论.
试题解析:(1)BD=AD,
理由:∵△ABC是等腰直角三角形,
∴∠BAC=∠ABC=45°.
∵∠CAD=∠CBD=15°
∴∠BAC-∠CAD=∠ABC-∠CBD=45°-15°=30°,
即∠DAB=∠DBA,
∴BD=AD;
(2)∵△ABC是等腰直角三角形,
∴AC=BC,∠ACB=90°,
∵在△ADC和△BDC中,
,
∴△ADC≌△BDC(SAS),
∴∠DCA=∠DCB,
∴∠DCA=∠ACB=×90°=45°;
(3)连结MC,
∵∠MDC=∠CAD+∠ACD,
∴∠MDC=15°+45°=60°.
∵DC=DM,
∴△DCM是等边三角形.
∴CD=CM=DM,∠CDM=∠DMC=∠DCM.
∵CE=CA,
∴∠CAE=∠CEA=15°,BC=CE,
∴∠ACE=150°
∴∠MCE=150°-45°-60°=45°,
∴∠MCE=∠DCB,
∵在△MCE和△DCB中,
,
∴△MCE≌△DCB(SAS),
∴ME=BD.
10、答案:
试题分析:先确定△CDF是等腰三角形,得出∠CFD=∠CDF=45°,因为不确定△BDE是以那两条边为腰的等腰三角形,故需讨论,①DE=DB,②BD=BE,③DE=BE,然后分别利用角的关系得出答案即可.
试题解析:∵△CDF中,∠C=90°,且△CDF是等腰三角形,
∴CF=CD,
∴∠CFD=∠CDF=45°,
设∠DAE=x°,由对称性可知,AF=FD,AE=DE,
∴∠FDA=∠CFD=22.5°,∠DEB=2x°,
分类如下:
①当DE=DB时,∠B=∠DEB=2x°,
由∠CDE=∠DEB+∠B,得45°+22.5°+x=4x,
解得:x=22.5°.此时∠B=2x=45°;
见图形(1),说明:图中AD应平分∠CAB.
②当BD=BE时,则∠B=(180°-4x)°,
由∠CDE=∠DEB+∠B得:45°+22.5°+x=2x+180°-4x,
解得x=37.5°,此时∠B=(180-4x)°=30°.
图形(2)说明:∠CAB=60°,∠CAD=22.5°.
③DE=BE时,则∠B=()°,
由∠CDE=∠DEB+∠B得,45°+22.5°+x=2x+,
此方程无解.
∴DE=BE不成立.
综上所述∠B=45°或30°.
11、答案:
试题分析:(1)求出∠CDB,根据轴对称得出∠EDC=∠CDB=60°,即可得出答案.
(2)过A作AM⊥AC交ED延长线于M,证△ADM≌△ADC,推出AC=AM=BC,证△AFM≌△CBG,即可推出答案.
(3)过A作AQ⊥CD交CD延长线于Q,求出DQ,求出CQ,证△AQC≌△CHB,推出BH=CQ即可.
试题解析:(1)∵∠ACB=90°,∠ACD=15°,
∴∠DCB=75°,
∵△ABC中,AC=BC,∠ACB=90°,
∴∠CAD=∠CBA=45°,
∴∠CDB=180°-45°-75°=60°,
∵点B、点E关于CD对称,
∴∠EDC=∠CDB=60°,
∴∠ADF=180°-60°-60°=60°;
(2)证明:过A作AM⊥AC交ED延长线于M,
则∠FAM=90°=∠BCG,∠MAD=90°-45°=45°=∠CAD,
∵∠MAD=45°,∠ADF=60°,
∴∠M=60°-45°=15°=∠ACD,
∵点B、点E关于CD对称,
∴CD⊥BE,
∴∠CHG=90°,
∵∠BCG=90°,
∴∠CBG+∠CGB=∠CGB+∠ACD=90°,
∴∠CBG=∠ACD=15°,
在△ACD和△AMD中,
,
∴△ACD≌△AMD(AAS),
∴AC=AM=BC,
在△FAM和△GCB中,
,
∴△FAM≌△GCB(ASA),
∴AF=CG;
(3)过A作AQ⊥CD交CD延长线于Q,
∵在△AQD中,∠Q=90°,∠QAD=90°-∠ADQ=90°-∠CDB=90°-60°=30°,AD=,
∴DQ=AD=,
∴CQ=+=,
在△AQC和△CHB中,
∴△AQC≌△CHB(AAS),
∴BH=CQ=.
故答案为:.
12、答案:
试题分析:由于△APQ为等腰三角形,∠A为底角或顶角不能确定,故应分∠A为底角和顶角两种情况进行讨论.
试题解析:①当∠A为等腰△AOQ的底角时,此时PQ=AQ,
∵∠A=30°,
∴∠AQP=∠A′QC=120°,
∵∠A′=45°,
∴∠A′CQ=180°-∠A′QC-∠A′=180°-120°-45°=15°,
由旋转的性质可知∠q=∠A′CQ=15°;
②当∠A为等腰△AOQ的顶角时,此时AP=AQ,
∵∠A=30°,
∴∠APQ=∠B′PQ===75°,
∵∠B′=90°-∠A=90°-30°=60°,
∴∠B′EP=∠BEC=180°-∠B′-∠B′PQ=180°-45°-75°=60°,
∵∠B=90°-∠A=90°-30°=60°,
∴∠q=180°-∠B-∠BEC=180°-60°-60°=60°.
故答案为:15°,60°.
13、答案:
试题分析:连接CD,由等腰直角三角形的性质用ASA证得△CFD≌△AED,△CED≌△BFD即可.
试题解析:证明:连接CD,
∵△ABC是等腰直角三角形,D是AB的中点,
∴CD=AD=BD,∠A=∠B=∠ACD=∠BCD=45°,CD⊥AB.
∵∠CDF+∠CDE=∠CDE+∠EDA=90°,
∴∠CDF=ADE.
∴△CDF≌△ADE.
同理△CED≌△BFD,
∴S△CDF=S△ADE,S△CED=S△BFD.
∴S四边形EDFC=S△ABC.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
