北师大版九年级数学上册 第1章 1.1菱形的性质和判定的应用 同步测试(word含答案)
文档属性
| 名称 | 北师大版九年级数学上册 第1章 1.1菱形的性质和判定的应用 同步测试(word含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 238.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-07 00:00:00 | ||
图片预览




文档简介
北师版九年级数学上册第一章特殊平行四边形
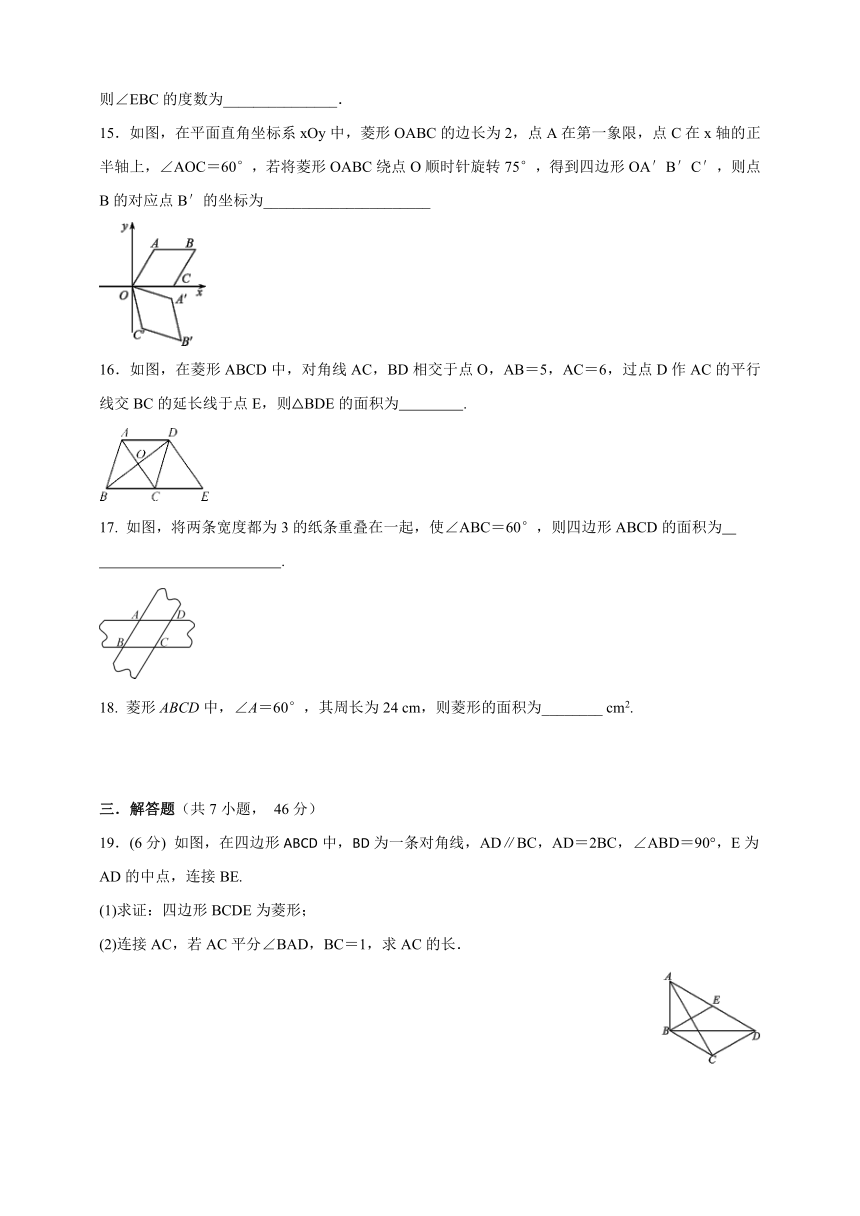
1.1菱形的性质和判定的应用
同步测试
题号
一
二
三
总分
得分
第Ⅰ卷(选择题)
一、选择题(共10小题,3
10=30)
1.如图,菱形ABCD的周长是20,对角线AC,BD相交于点O,若BD=6,则菱形ABCD的面积是(
)
A.6
B.12
C.24
D.48
2.如图,已知某广场菱形花坛的边长是6
m,∠BAD=60°,则花坛的面积为(
)
A.18
m2
B.18
m2
C.36
m2
D.36
m2
3.如图,在菱形ABCD中,AB=5,对角线AC与BD相交于点O,且AC∶BD=3∶4,AE⊥CD于点E,则AE的长是(
)
A.4
B.
C.5
D.
4.如图,添加下列条件仍然不能使?ABCD成为菱形的是(
)
A.AB=BC
B.AC⊥BD
C.∠ABC=90°
D.∠1=∠2
5.
剪两张对边平行且宽度相同的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是(
)
A.∠ABC=∠ADC,∠BAD=∠BCD
B.AB=BC
C.AB=CD,AD=BC
D.∠DAB+∠BCD=180°
6.
菱形的一个内角为120°,边长为8,那么它较短的对角线长为(
)
A.3
B.4
C.8
D.6
7.
如图,在菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是(
)
A.4
B.3
C.2
D.
8.
如图,已知四边形ABCD的四边都相等,等边三角形AEF的顶点E,F分别在BC,CD上,且AE=AB,则∠C的度数为(
)
A.100°
B.105°
C.110°
D.120°
9.如图
6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,边长为1,A,B都在格点上,则AB的长为(
)
A.
B.
C.
D.
10.
如图,在给定的一张平行四边形纸片ABCD上作一个菱形,甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于点M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠BAD,∠ABC的平分线AE,BF,分别交BC,AD于点E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断(
)
A.甲正确,乙错误
B.甲错误,乙正确
C.甲、乙均正确
D.甲、乙均错误
第Ⅱ卷(非选择题)
二.填空题(共8小题,3
8=24)11.
11.
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于____.
12.
如图所示,在菱形ABCD中,BE⊥AD于点E,BF⊥CD于点F,且AE=DE,则∠EBF等于____.
13.如图,两条笔直的公路l1,l2相交于点O,村庄C的村民在公路的旁边建了三个加工厂A,B,D,已知AB=BC=CD=DA=5
km,村庄C到公路l1的距离为4
km,则村庄C到公路l2的距离是
km.
14.
在菱形ABCD中,∠A=30°,在同一平面内,以对角线BD为底边作顶角为120°的等腰△BDE,则∠EBC的度数为_______________.
15.如图,在平面直角坐标系xOy中,菱形OABC的边长为2,点A在第一象限,点C在x轴的正半轴上,∠AOC=60°,若将菱形OABC绕点O顺时针旋转75°,得到四边形OA′B′C′,则点B的对应点B′的坐标为______________________
16.如图,在菱形ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,过点D作AC的平行线交BC的延长线于点E,则△BDE的面积为
.
17.
如图,将两条宽度都为3的纸条重叠在一起,使∠ABC=60°,则四边形ABCD的面积为
.
18.
菱形ABCD中,∠A=60°,其周长为24
cm,则菱形的面积为________
cm2.
三.解答题(共7小题,
46分)
19.(6分)
如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.
20.
(6分)
如图,在四边形ABCD中,AB=CD,M,N,P,Q分别是AD,BC,BD,AC的中点,连接MN,PQ,请你探索MN与PQ的关系,并证明你的结论.
21.
(6分)如图,四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F.
(1)求证:△AOE≌△COF;
(2)若∠EOD=30°,求CE的长.
22.(6分)
如图,在?ABCD中,E,F分别是AD,BC上的点,O是AC的中点,且AC⊥EF.求证:四边形AECF是菱形.
23.(6分)
如图30所示,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=a.
(1)求∠ABC的度数;
(2)求对角线AC的长;
(3)求菱形ABCD的面积.
24.(8分)
如图32,在四边形ABCD中,AB=AD,BD平分∠ABC,AC⊥BD,垂足为O.
(1)求证:四边形ABCD是菱形;
(2)若CD=3,BD=2,求四边形ABCD的面积.
25.(8分)
对一张长方形纸片ABCD进行折叠,具体操作如下:
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再一次折叠,使点A落在MN上的点A′处,并使折痕经过点B,得到折痕BE,同时,得到线段BA′,EA′,展开,如图①;
第三步:再沿EA′所在的直线折叠,点B落在AD上的点B′处,得到折痕EF,同时得到线段B′F,展开,如图②.
求证:(1)∠ABE=30°;
(2)四边形BFB′E为菱形.
参考答案
1-5
CBBCD
6-10
CBACC
11.
12.
60°
13.
4
14.
45°或105°
15.
(,-)
16.
24
17.
6
18.
18
19.
(1)证明:∵AD=2BC,E为AD的中点,∴DE=BC,
∵AD∥BC,∴四边形BCDE是平行四边形,
∵∠ABD=90°,AE=DE,∴BE=DE,∴四边形BCDE是菱形
(2)解:∵AD∥BC,AC平分∠BAD,∴∠BAC=∠DAC=∠BCA,
∴AB=BC=1,∵AD=2AB=2BC=2,∠ABD=90°,
E为AD的中点,∴AB=AE=BE,∴△ABE是等边三角形,
∴∠ADB=30°,∴∠DAC=30°,∠ADC=60°,
在Rt△ACD中,∵AD=2,∴CD=1,AC=
20.
解:MN与PQ互相垂直平分,
证明如下:
如图,连接PM,MQ,NP,NQ.
在△DAB中,
∵P,M分别是BD,AD的中点,
∴PM=AB.
同理:PN=CD,MQ=CD,
NQ=AB.
又∵AB=CD,
∴PM=PN=NQ=MQ,
∴四边形MPNQ是菱形,
∴MN与PQ互相垂直平分
21.
解:(1)∵四边形ABCD是菱形,
∴AO=CO,AD∥BC,
∴∠OAE=∠OCF,
又∵∠AOE=∠COF,
∴△AOE≌△COF(ASA)
(2)∵∠BAD=60°,
∴∠DAO=∠BAD=30°,
∵∠EOD=30°,
∴∠AOE=90°-30°=60°,
∴∠AEF=180°-∠DAO-∠AOE=180°-30°-60°=90°.
∵菱形ABCD的边长为2,∠DAO=30°,
∴OD=AD=1,
∴AO==,
可求AE=CF=,
EF=2OE=,
在Rt△CEF中,
CE===
22.
解:(1)∵EF垂直平分AC,FA=FC,EA=EC.
∴∠AFE=∠CFE,
∠AEF=∠CEF.
又∵四边形ABCD是平行四边形,
∴AD∥BC.∠AFE=∠CEF=∠AEF,
∴AF=AE,AE=EC=CF=FA,
∴四边形AECF是菱形
(2)∵AC⊥CD,AC⊥EF,
∴EF∥CD.又∵AB∥CD,
∴AB∥EF.∴四边形ABEF为平行四边形.
∴EF=AB=6.∵AC⊥CD,∴AB⊥AC.在Rt△ABC中,由勾股定理,得AC=8.
∴四边形AECF的面积为AC·EF=×8×6=24
23.
解:(1)在菱形ABCD中,AD=AB.
∵DE⊥AB,AE=BE,∴AD=BD,
∴AD=BD=AB,∴△ABD为等边三角形,
∴∠ABD=60°,∴∠ABC=2∠ABD=120°.
(2)在菱形ABCD中,AC与BD互相垂直平分.
∵BD=AB=AD=a,∠BAC=∠BAD=30°,
∴OB=a,∴OA=a,∴AC=
a.
(3)S菱形ABCD=AC·BD=×
a·a=a2.
24.
解:(1)证明:∵AB=AD,∴∠ABD=∠ADB.
∵BD平分∠ABC,∴∠ABD=∠CBD,
∴∠ADB=∠CBD.
∵AC⊥BD,AB=AD,∴OB=OD.
在△AOD与△COB中,∠AOD=∠COB,OD=OB,∠ADO=∠CBO,
∴△AOD≌△COB,∴OA=OC.
∴四边形ABCD是平行四边形.
又∵AC⊥BD,∴四边形ABCD是菱形.
(2)∵四边形ABCD是菱形,∴OD=BD=,
∴OC==2,∴AC=2OC=4,
∴S菱形ABCD=AC·BD=4.
25.
证明:(1)∵第二步折叠,使点A落在MN上的点A′处,
并使折痕经过点B,得到折痕BE,∴∠AEB=∠A′EB.
∵第三步折叠,点B落在AD上的点B′处,得到折痕EF,
同时得到线段B′F,∴∠A′EB=∠FEB′.
∵∠AEB+∠A′EB+∠FEB′=180°,
∴∠AEB=∠A′EB=∠FEB′=60°.∴∠ABE=90°-∠AEB=30°
(2)∵∠A′EB=∠FEB′=60°,EB′∥BF,
∴∠A′EB=∠FEB′=∠BFE=∠EFB′=60°.
∴△BEF和△EFB′是等边三角形.∴BE=BF=EF=EB′=FB′.
∴四边形BFB′E为菱形
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
1.1菱形的性质和判定的应用
同步测试
题号
一
二
三
总分
得分
第Ⅰ卷(选择题)
一、选择题(共10小题,3
10=30)
1.如图,菱形ABCD的周长是20,对角线AC,BD相交于点O,若BD=6,则菱形ABCD的面积是(
)
A.6
B.12
C.24
D.48
2.如图,已知某广场菱形花坛的边长是6
m,∠BAD=60°,则花坛的面积为(
)
A.18
m2
B.18
m2
C.36
m2
D.36
m2
3.如图,在菱形ABCD中,AB=5,对角线AC与BD相交于点O,且AC∶BD=3∶4,AE⊥CD于点E,则AE的长是(
)
A.4
B.
C.5
D.
4.如图,添加下列条件仍然不能使?ABCD成为菱形的是(
)
A.AB=BC
B.AC⊥BD
C.∠ABC=90°
D.∠1=∠2
5.
剪两张对边平行且宽度相同的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是(
)
A.∠ABC=∠ADC,∠BAD=∠BCD
B.AB=BC
C.AB=CD,AD=BC
D.∠DAB+∠BCD=180°
6.
菱形的一个内角为120°,边长为8,那么它较短的对角线长为(
)
A.3
B.4
C.8
D.6
7.
如图,在菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是(
)
A.4
B.3
C.2
D.
8.
如图,已知四边形ABCD的四边都相等,等边三角形AEF的顶点E,F分别在BC,CD上,且AE=AB,则∠C的度数为(
)
A.100°
B.105°
C.110°
D.120°
9.如图
6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,边长为1,A,B都在格点上,则AB的长为(
)
A.
B.
C.
D.
10.
如图,在给定的一张平行四边形纸片ABCD上作一个菱形,甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于点M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠BAD,∠ABC的平分线AE,BF,分别交BC,AD于点E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断(
)
A.甲正确,乙错误
B.甲错误,乙正确
C.甲、乙均正确
D.甲、乙均错误
第Ⅱ卷(非选择题)
二.填空题(共8小题,3
8=24)11.
11.
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于____.
12.
如图所示,在菱形ABCD中,BE⊥AD于点E,BF⊥CD于点F,且AE=DE,则∠EBF等于____.
13.如图,两条笔直的公路l1,l2相交于点O,村庄C的村民在公路的旁边建了三个加工厂A,B,D,已知AB=BC=CD=DA=5
km,村庄C到公路l1的距离为4
km,则村庄C到公路l2的距离是
km.
14.
在菱形ABCD中,∠A=30°,在同一平面内,以对角线BD为底边作顶角为120°的等腰△BDE,则∠EBC的度数为_______________.
15.如图,在平面直角坐标系xOy中,菱形OABC的边长为2,点A在第一象限,点C在x轴的正半轴上,∠AOC=60°,若将菱形OABC绕点O顺时针旋转75°,得到四边形OA′B′C′,则点B的对应点B′的坐标为______________________
16.如图,在菱形ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,过点D作AC的平行线交BC的延长线于点E,则△BDE的面积为
.
17.
如图,将两条宽度都为3的纸条重叠在一起,使∠ABC=60°,则四边形ABCD的面积为
.
18.
菱形ABCD中,∠A=60°,其周长为24
cm,则菱形的面积为________
cm2.
三.解答题(共7小题,
46分)
19.(6分)
如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.
20.
(6分)
如图,在四边形ABCD中,AB=CD,M,N,P,Q分别是AD,BC,BD,AC的中点,连接MN,PQ,请你探索MN与PQ的关系,并证明你的结论.
21.
(6分)如图,四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F.
(1)求证:△AOE≌△COF;
(2)若∠EOD=30°,求CE的长.
22.(6分)
如图,在?ABCD中,E,F分别是AD,BC上的点,O是AC的中点,且AC⊥EF.求证:四边形AECF是菱形.
23.(6分)
如图30所示,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=a.
(1)求∠ABC的度数;
(2)求对角线AC的长;
(3)求菱形ABCD的面积.
24.(8分)
如图32,在四边形ABCD中,AB=AD,BD平分∠ABC,AC⊥BD,垂足为O.
(1)求证:四边形ABCD是菱形;
(2)若CD=3,BD=2,求四边形ABCD的面积.
25.(8分)
对一张长方形纸片ABCD进行折叠,具体操作如下:
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再一次折叠,使点A落在MN上的点A′处,并使折痕经过点B,得到折痕BE,同时,得到线段BA′,EA′,展开,如图①;
第三步:再沿EA′所在的直线折叠,点B落在AD上的点B′处,得到折痕EF,同时得到线段B′F,展开,如图②.
求证:(1)∠ABE=30°;
(2)四边形BFB′E为菱形.
参考答案
1-5
CBBCD
6-10
CBACC
11.
12.
60°
13.
4
14.
45°或105°
15.
(,-)
16.
24
17.
6
18.
18
19.
(1)证明:∵AD=2BC,E为AD的中点,∴DE=BC,
∵AD∥BC,∴四边形BCDE是平行四边形,
∵∠ABD=90°,AE=DE,∴BE=DE,∴四边形BCDE是菱形
(2)解:∵AD∥BC,AC平分∠BAD,∴∠BAC=∠DAC=∠BCA,
∴AB=BC=1,∵AD=2AB=2BC=2,∠ABD=90°,
E为AD的中点,∴AB=AE=BE,∴△ABE是等边三角形,
∴∠ADB=30°,∴∠DAC=30°,∠ADC=60°,
在Rt△ACD中,∵AD=2,∴CD=1,AC=
20.
解:MN与PQ互相垂直平分,
证明如下:
如图,连接PM,MQ,NP,NQ.
在△DAB中,
∵P,M分别是BD,AD的中点,
∴PM=AB.
同理:PN=CD,MQ=CD,
NQ=AB.
又∵AB=CD,
∴PM=PN=NQ=MQ,
∴四边形MPNQ是菱形,
∴MN与PQ互相垂直平分
21.
解:(1)∵四边形ABCD是菱形,
∴AO=CO,AD∥BC,
∴∠OAE=∠OCF,
又∵∠AOE=∠COF,
∴△AOE≌△COF(ASA)
(2)∵∠BAD=60°,
∴∠DAO=∠BAD=30°,
∵∠EOD=30°,
∴∠AOE=90°-30°=60°,
∴∠AEF=180°-∠DAO-∠AOE=180°-30°-60°=90°.
∵菱形ABCD的边长为2,∠DAO=30°,
∴OD=AD=1,
∴AO==,
可求AE=CF=,
EF=2OE=,
在Rt△CEF中,
CE===
22.
解:(1)∵EF垂直平分AC,FA=FC,EA=EC.
∴∠AFE=∠CFE,
∠AEF=∠CEF.
又∵四边形ABCD是平行四边形,
∴AD∥BC.∠AFE=∠CEF=∠AEF,
∴AF=AE,AE=EC=CF=FA,
∴四边形AECF是菱形
(2)∵AC⊥CD,AC⊥EF,
∴EF∥CD.又∵AB∥CD,
∴AB∥EF.∴四边形ABEF为平行四边形.
∴EF=AB=6.∵AC⊥CD,∴AB⊥AC.在Rt△ABC中,由勾股定理,得AC=8.
∴四边形AECF的面积为AC·EF=×8×6=24
23.
解:(1)在菱形ABCD中,AD=AB.
∵DE⊥AB,AE=BE,∴AD=BD,
∴AD=BD=AB,∴△ABD为等边三角形,
∴∠ABD=60°,∴∠ABC=2∠ABD=120°.
(2)在菱形ABCD中,AC与BD互相垂直平分.
∵BD=AB=AD=a,∠BAC=∠BAD=30°,
∴OB=a,∴OA=a,∴AC=
a.
(3)S菱形ABCD=AC·BD=×
a·a=a2.
24.
解:(1)证明:∵AB=AD,∴∠ABD=∠ADB.
∵BD平分∠ABC,∴∠ABD=∠CBD,
∴∠ADB=∠CBD.
∵AC⊥BD,AB=AD,∴OB=OD.
在△AOD与△COB中,∠AOD=∠COB,OD=OB,∠ADO=∠CBO,
∴△AOD≌△COB,∴OA=OC.
∴四边形ABCD是平行四边形.
又∵AC⊥BD,∴四边形ABCD是菱形.
(2)∵四边形ABCD是菱形,∴OD=BD=,
∴OC==2,∴AC=2OC=4,
∴S菱形ABCD=AC·BD=4.
25.
证明:(1)∵第二步折叠,使点A落在MN上的点A′处,
并使折痕经过点B,得到折痕BE,∴∠AEB=∠A′EB.
∵第三步折叠,点B落在AD上的点B′处,得到折痕EF,
同时得到线段B′F,∴∠A′EB=∠FEB′.
∵∠AEB+∠A′EB+∠FEB′=180°,
∴∠AEB=∠A′EB=∠FEB′=60°.∴∠ABE=90°-∠AEB=30°
(2)∵∠A′EB=∠FEB′=60°,EB′∥BF,
∴∠A′EB=∠FEB′=∠BFE=∠EFB′=60°.
∴△BEF和△EFB′是等边三角形.∴BE=BF=EF=EB′=FB′.
∴四边形BFB′E为菱形
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
