北师大版七年级第一章 丰富的图形世界学案(无答案)
文档属性
| 名称 | 北师大版七年级第一章 丰富的图形世界学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 325.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-08 00:00:00 | ||
图片预览



文档简介
七年级第一章
丰富的图形世界
知识点1:生活中的立体图形
1
.柱体
①
正方体:它有
8
个顶点、
12
条棱、
6
个面,其中
12
条梭长都相等,
6
个面都是相等的正方形.
②
长方体:它有
8
个顶点、
12
条棱、
6
个面,其中各个面都是长方形(或正方形),且相对的两个面大小相等.
③
棱柱体:
如图(
1
)
(
2
)
,图中上下两个面称棱柱的底面,周围的面称棱柱的侧面,面与面的交线是棱柱的梭.其中侧面与侧面的交线是侧棱,棱与棱的交点是顶点.
正方体和长方体是特殊的梭柱,它们都是四棱柱.正方体是特殊的长方体.
④
圆柱:图(
3
)中上下两个圆面是圆柱的底面,这两个底面是半径相同的圆,周围是圆柱的侧面.棱柱和圆柱统称柱体.
2
.锥体
①
圆锥:如图(
4
)
图中的圆面是圆锥的一个底面,中间曲面是圃锥的一个侧面,圆锥还有一个顶点.
②
棱锥:如图(
5
)
图中下面多边形面是梭锥的一个底面,其余各三角形面是棱锥的侧面,各侧面的交线是棱锥的侧棱,各侧棱的交点是棱锥的顶点.棱锥和回锥统称锥体.
3
.台体
①
圆台:
如图6
图中上下两个不同的国面是圆台的底面,中间曲面是圆台的一个侧面.
②
棱台:
如图
7
图中上、下两个多边形是棱台的底面,其余四边形面是棱台的侧面,各侧面的交线是棱台的侧棱,底面和侧面誉。的交线是棱,梭与侧棱的交点是棱台的顶点.
4
.球体:
如图(
8
)
图中半圆绕其直径旋转而成的几何体,如篮球、足球等都是球体.
例1
将下列图形与对应的图形名称用线连接:
圆
柱
圆
锥
球
体
棱
柱
长方体
知识点2
图形是由点、线、面构成的
1、点、线、面之间的关系
(1)有光滑的黑板面,平静的游泳池的水面,都是平的,而球面,水桶的侧面都是曲的,因此,我们知道,面分为________和________.
(2)再观察现代化城市的交通图,你可以看到立交桥,其中最上一层的立交桥画面上的部分是直的,而下一层是弯的,如果我们将这些公路抽象成线就可以知道线也分为两种_______和_______
2、点动成线,线动成面,面动成体
(1)给出一张地图大家能找出图中的点和线吗?发现点和线的一种关系:线和线相交可以得到_____________
(2)侧墙面与水平墙面中的面和线。发现面和线的一种关系,面面相交可以得到_____________
(3)如果给出一个几何体(长方体),大家能找出他的点、线和面吗?从而有面和面相交可以得到_______。
例题
1
、几何图形由_____、_____、_____构成,面有______面和______面之分。
2、面与面相交得______,线与线相交得______。
3
、点动成______、线动成______、面动成______。
4
、长方体是由______个面围成的,圆柱是______个面围成的,圆锥是由______个面围成的。其中围成圆锥的面有______面,也有______面.
知识点3
展开与折叠
(1)在棱柱中,任何相邻两个面的交线都叫做▁▁▁▁▁。棱柱的所有▁▁▁▁▁都相等。棱柱的▁▁▁▁▁相同。▁▁▁▁▁的形状都是长方形。
(2)一底面是正方形的棱柱高为4cm,正方形的边长都为2cm,则此棱柱共有▁▁▁▁▁条棱,所有棱长之和为▁▁▁▁▁cm。
正方体11种展开图
例1
如下图所示,图形能围成一个正方体的是(
)
A
B
C
知识点4
截一个几何体
[例1]
下图中的截面形状分别是什么?
(1)
(2)
[例2]、用平面截下列几何体,找出相应的截面形状.
知识点5
从不同方向看物体的形状
从上面看
知识点6
生活中的平面图形
1.多边形的定义:三角形、四边形、五边形等都是多边形,它们都是由一些不在同一条直线上的线段依次首尾相连组成的封闭图形.(边长与角都分别相等的多边形叫正多边形).
2.多边形的分割:
设一个多边形的边数为n(n≥3)
,从这个n边形的一个顶点出发,分别连接这个顶点与其余各顶点,可以得到________条线段,这些线段又把这个n边形分割成_________个三角形.
多边形
三角形
四边形
五边形
…
n边形
线段数
三角形个数
3.扇形与弧的定义及区别
(1)弧:圆周或曲线上任意一段叫弧.
(2)扇形:一条弧和经过这条弧两端的两条半径所围成的图形叫扇形
(3)扇形与弧的区别:弧是一段曲线,而扇形是一个面.
4.从多边形的一个顶点出发,与各顶点连线连成的对角线条数为
m
,可分成的三角形的个数为n,如下图所示.
仿照上面的方法画线,请你猜想出:
(
1
)
100
边形中的m=____________
,
n=______________
。
(
2
)
a
(
a
>
3
)边形中的
m
=___________
,n=___________
。
练习从一个多边形的顶点出发,连接这个顶点与其余的顶点,得到分割成的十个三角形,则这个多边形是_______边形.
巩固练习
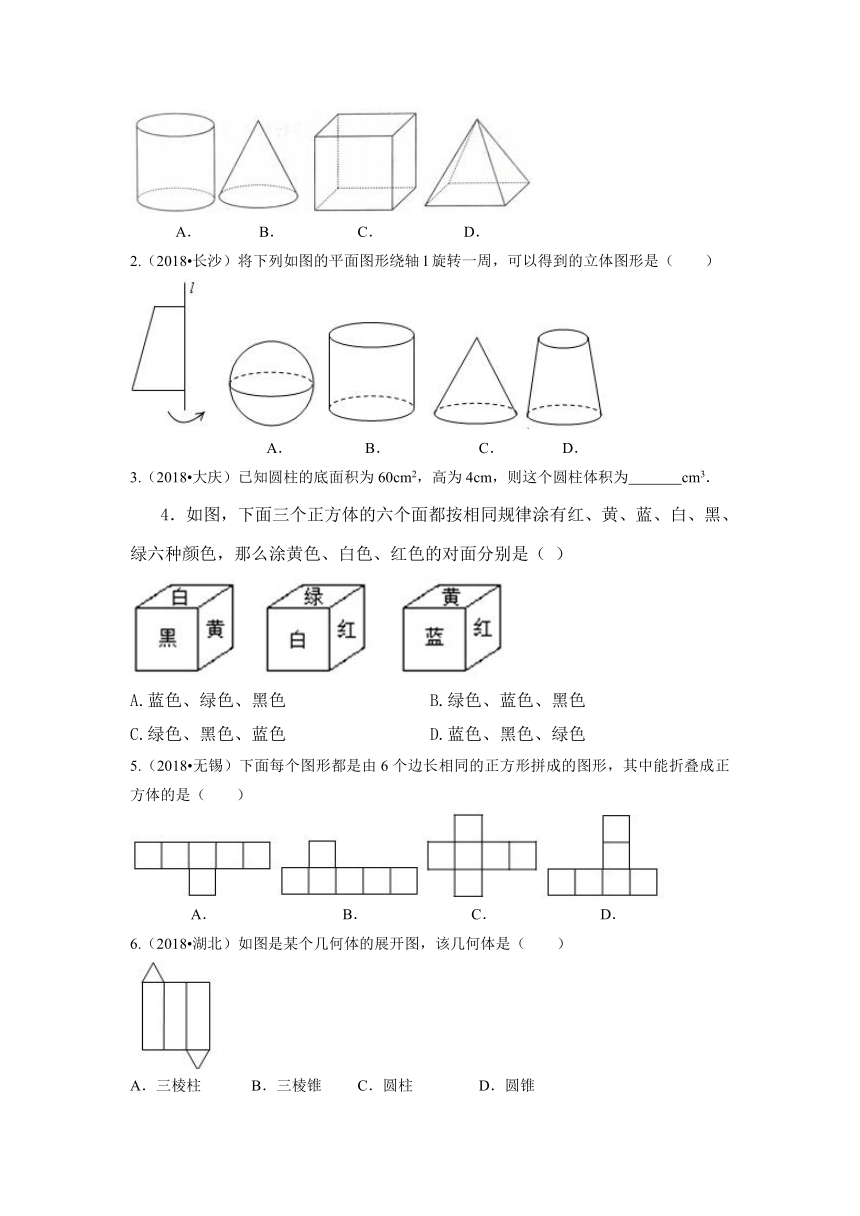
1.(2018?北京)下列几何体中,是圆柱的为( )
A.
B.
C.
D.
2.(2018?长沙)将下列如图的平面图形绕轴l旋转一周,可以得到的立体图形是( )
A.
B.
C.
D.
3.(2018?大庆)已知圆柱的底面积为60cm2,高为4cm,则这个圆柱体积为
cm3.
4.如图,下面三个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色,那么涂黄色、白色、红色的对面分别是(
)
A.蓝色、绿色、黑色
B.绿色、蓝色、黑色
C.绿色、黑色、蓝色
D.蓝色、黑色、绿色
5.(2018?无锡)下面每个图形都是由6个边长相同的正方形拼成的图形,其中能折叠成正方体的是( )
A.
B.
C.
D.
6.(2018?湖北)如图是某个几何体的展开图,该几何体是( )
A.三棱柱
B.三棱锥
C.圆柱
D.圆锥
7(2018?陕西)如图,是一个几何体的表面展开图,则该几何体是( )
A.正方体
B.长方体
C.三棱柱
D.四棱锥
8.如图是一个几何体的三视图,则这个几何体是(
)
主视图
左视图
俯视图
A.
B.
C.
D.
9.(2018?南京)用一个平面去截正方体(如图),下列关于截面(截出的面)的形状的结论:
①可能是锐角三角形;
②可能是直角三角形;
③可能是钝角三角形;
④可能是平行四边形.
其中所有正确结论的序号是( )
A.①②
B.①④
C.①②④
D.①②③④
10.(2018?烟台)由5个棱长为1的小正方体组成的几何体如图放置,一面着地,两面靠墙.如果要将露出来的部分涂色,则涂色部分的面积为( )
A.9
B.11
C.14
D.18
拓展提高
1.(2018?呼和浩特)下面是几个一样的小正方体摆出的立体图形的三视图,由三视图可知小正方体的个数为( )
A.6个
B.5个
C.4个
D.3个
2.(2018?荆门)某几何体由若干个大小相同的小正方体搭成,其主视图与左视图如图所示,则搭成这个几何体的小正方体最少有( )
A.4个
B.5个
C.6个
D.7个
3.一个几何体的三个视图如图所示(单位:cm).
(1)写出这个几何体的名称:
;
(2)若其俯视图为正方形,根据图中数据计算这个几何体的表面积.
家庭作业
一、选择题
1.一个正方体的截面不可能是(
)
A.三角形
B.梯形
C.五边形
D.七边形
2.如图是一个正方体的展开图,那么折成正方体后,“爱”字所对的面的字是(
)
A.美
B.丽
C.中
D.江
3.下面的图形经过折叠能围成正方体的是(
)
A.
B.
C.
D.
4.如图是由一些相同的小正方体构成的立体图形分别从正面、左面看到的形状,那么构成这个立体图形的小正方体最少有(
)
A.3个
B.4个
C.6个
D.7个
5.如图中几何体由一些完全相同的小立方体组成,从上面看到图形的形状是(
)
A.
B.
C.
D.
6.下面几何体的截面不可能是长方形的是( )
A.长方体
B.正方体
C.圆锥
D.圆柱
7.下列说法中,错误的是( )
A.点动成线
B.线动成面
C.面动成体
D.棱柱的棱长都相等
8.已知从三个方向看到的几何体的形状图如图10所示,那么这个几何体的侧面积是( )
A.4π
B.6π
C.8π
D.12π
9.如图是从上面看由几个大小相同的小立方块所搭成的几何体得到的形状图,小正方形中的数字表示在该位置的小立方块的个数,则从正面看到的几何体的形状图是( )
A.
B.
C.
D.
10.在一仓库里堆放着若干个大小相同的正方体小货箱,仓库管理员将从三个方向看到的物体的形状图画了出来,如图所示,则这堆正方体小货箱共有( )
A.11个
B.10个
C.9个
D.8个
11.一位画家把边长为1m的7个相同正方体摆成如图的形式,然后把露出的表面涂上颜色,则涂色面积为________m.
12.如图,正方形ABDC的边长为3,以直线AB为轴,将正方形旋转一周,形成一个几何体,则从正面看到的形状图的周长是_______.
13.请写出图中几何体中截面的形状.
①________;②________;③________.
14.已知图为一几何体从不同方向看的图形:
写出这个几何体的名称;
任意画出这个几何体的一种表面展开图;
若长方形的高为厘米,三角形的边长为厘米,求这个几何体的侧面积.
15.用小立方体搭成一个几何体,从正面和上面看到该几何体的形状图如图所示,搭建这样的几何体最多要几个小立方体?最少要几个小立方体?并画出最多和最少时从左面看到的形状图.
丰富的图形世界
知识点1:生活中的立体图形
1
.柱体
①
正方体:它有
8
个顶点、
12
条棱、
6
个面,其中
12
条梭长都相等,
6
个面都是相等的正方形.
②
长方体:它有
8
个顶点、
12
条棱、
6
个面,其中各个面都是长方形(或正方形),且相对的两个面大小相等.
③
棱柱体:
如图(
1
)
(
2
)
,图中上下两个面称棱柱的底面,周围的面称棱柱的侧面,面与面的交线是棱柱的梭.其中侧面与侧面的交线是侧棱,棱与棱的交点是顶点.
正方体和长方体是特殊的梭柱,它们都是四棱柱.正方体是特殊的长方体.
④
圆柱:图(
3
)中上下两个圆面是圆柱的底面,这两个底面是半径相同的圆,周围是圆柱的侧面.棱柱和圆柱统称柱体.
2
.锥体
①
圆锥:如图(
4
)
图中的圆面是圆锥的一个底面,中间曲面是圃锥的一个侧面,圆锥还有一个顶点.
②
棱锥:如图(
5
)
图中下面多边形面是梭锥的一个底面,其余各三角形面是棱锥的侧面,各侧面的交线是棱锥的侧棱,各侧棱的交点是棱锥的顶点.棱锥和回锥统称锥体.
3
.台体
①
圆台:
如图6
图中上下两个不同的国面是圆台的底面,中间曲面是圆台的一个侧面.
②
棱台:
如图
7
图中上、下两个多边形是棱台的底面,其余四边形面是棱台的侧面,各侧面的交线是棱台的侧棱,底面和侧面誉。的交线是棱,梭与侧棱的交点是棱台的顶点.
4
.球体:
如图(
8
)
图中半圆绕其直径旋转而成的几何体,如篮球、足球等都是球体.
例1
将下列图形与对应的图形名称用线连接:
圆
柱
圆
锥
球
体
棱
柱
长方体
知识点2
图形是由点、线、面构成的
1、点、线、面之间的关系
(1)有光滑的黑板面,平静的游泳池的水面,都是平的,而球面,水桶的侧面都是曲的,因此,我们知道,面分为________和________.
(2)再观察现代化城市的交通图,你可以看到立交桥,其中最上一层的立交桥画面上的部分是直的,而下一层是弯的,如果我们将这些公路抽象成线就可以知道线也分为两种_______和_______
2、点动成线,线动成面,面动成体
(1)给出一张地图大家能找出图中的点和线吗?发现点和线的一种关系:线和线相交可以得到_____________
(2)侧墙面与水平墙面中的面和线。发现面和线的一种关系,面面相交可以得到_____________
(3)如果给出一个几何体(长方体),大家能找出他的点、线和面吗?从而有面和面相交可以得到_______。
例题
1
、几何图形由_____、_____、_____构成,面有______面和______面之分。
2、面与面相交得______,线与线相交得______。
3
、点动成______、线动成______、面动成______。
4
、长方体是由______个面围成的,圆柱是______个面围成的,圆锥是由______个面围成的。其中围成圆锥的面有______面,也有______面.
知识点3
展开与折叠
(1)在棱柱中,任何相邻两个面的交线都叫做▁▁▁▁▁。棱柱的所有▁▁▁▁▁都相等。棱柱的▁▁▁▁▁相同。▁▁▁▁▁的形状都是长方形。
(2)一底面是正方形的棱柱高为4cm,正方形的边长都为2cm,则此棱柱共有▁▁▁▁▁条棱,所有棱长之和为▁▁▁▁▁cm。
正方体11种展开图
例1
如下图所示,图形能围成一个正方体的是(
)
A
B
C
知识点4
截一个几何体
[例1]
下图中的截面形状分别是什么?
(1)
(2)
[例2]、用平面截下列几何体,找出相应的截面形状.
知识点5
从不同方向看物体的形状
从上面看
知识点6
生活中的平面图形
1.多边形的定义:三角形、四边形、五边形等都是多边形,它们都是由一些不在同一条直线上的线段依次首尾相连组成的封闭图形.(边长与角都分别相等的多边形叫正多边形).
2.多边形的分割:
设一个多边形的边数为n(n≥3)
,从这个n边形的一个顶点出发,分别连接这个顶点与其余各顶点,可以得到________条线段,这些线段又把这个n边形分割成_________个三角形.
多边形
三角形
四边形
五边形
…
n边形
线段数
三角形个数
3.扇形与弧的定义及区别
(1)弧:圆周或曲线上任意一段叫弧.
(2)扇形:一条弧和经过这条弧两端的两条半径所围成的图形叫扇形
(3)扇形与弧的区别:弧是一段曲线,而扇形是一个面.
4.从多边形的一个顶点出发,与各顶点连线连成的对角线条数为
m
,可分成的三角形的个数为n,如下图所示.
仿照上面的方法画线,请你猜想出:
(
1
)
100
边形中的m=____________
,
n=______________
。
(
2
)
a
(
a
>
3
)边形中的
m
=___________
,n=___________
。
练习从一个多边形的顶点出发,连接这个顶点与其余的顶点,得到分割成的十个三角形,则这个多边形是_______边形.
巩固练习
1.(2018?北京)下列几何体中,是圆柱的为( )
A.
B.
C.
D.
2.(2018?长沙)将下列如图的平面图形绕轴l旋转一周,可以得到的立体图形是( )
A.
B.
C.
D.
3.(2018?大庆)已知圆柱的底面积为60cm2,高为4cm,则这个圆柱体积为
cm3.
4.如图,下面三个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色,那么涂黄色、白色、红色的对面分别是(
)
A.蓝色、绿色、黑色
B.绿色、蓝色、黑色
C.绿色、黑色、蓝色
D.蓝色、黑色、绿色
5.(2018?无锡)下面每个图形都是由6个边长相同的正方形拼成的图形,其中能折叠成正方体的是( )
A.
B.
C.
D.
6.(2018?湖北)如图是某个几何体的展开图,该几何体是( )
A.三棱柱
B.三棱锥
C.圆柱
D.圆锥
7(2018?陕西)如图,是一个几何体的表面展开图,则该几何体是( )
A.正方体
B.长方体
C.三棱柱
D.四棱锥
8.如图是一个几何体的三视图,则这个几何体是(
)
主视图
左视图
俯视图
A.
B.
C.
D.
9.(2018?南京)用一个平面去截正方体(如图),下列关于截面(截出的面)的形状的结论:
①可能是锐角三角形;
②可能是直角三角形;
③可能是钝角三角形;
④可能是平行四边形.
其中所有正确结论的序号是( )
A.①②
B.①④
C.①②④
D.①②③④
10.(2018?烟台)由5个棱长为1的小正方体组成的几何体如图放置,一面着地,两面靠墙.如果要将露出来的部分涂色,则涂色部分的面积为( )
A.9
B.11
C.14
D.18
拓展提高
1.(2018?呼和浩特)下面是几个一样的小正方体摆出的立体图形的三视图,由三视图可知小正方体的个数为( )
A.6个
B.5个
C.4个
D.3个
2.(2018?荆门)某几何体由若干个大小相同的小正方体搭成,其主视图与左视图如图所示,则搭成这个几何体的小正方体最少有( )
A.4个
B.5个
C.6个
D.7个
3.一个几何体的三个视图如图所示(单位:cm).
(1)写出这个几何体的名称:
;
(2)若其俯视图为正方形,根据图中数据计算这个几何体的表面积.
家庭作业
一、选择题
1.一个正方体的截面不可能是(
)
A.三角形
B.梯形
C.五边形
D.七边形
2.如图是一个正方体的展开图,那么折成正方体后,“爱”字所对的面的字是(
)
A.美
B.丽
C.中
D.江
3.下面的图形经过折叠能围成正方体的是(
)
A.
B.
C.
D.
4.如图是由一些相同的小正方体构成的立体图形分别从正面、左面看到的形状,那么构成这个立体图形的小正方体最少有(
)
A.3个
B.4个
C.6个
D.7个
5.如图中几何体由一些完全相同的小立方体组成,从上面看到图形的形状是(
)
A.
B.
C.
D.
6.下面几何体的截面不可能是长方形的是( )
A.长方体
B.正方体
C.圆锥
D.圆柱
7.下列说法中,错误的是( )
A.点动成线
B.线动成面
C.面动成体
D.棱柱的棱长都相等
8.已知从三个方向看到的几何体的形状图如图10所示,那么这个几何体的侧面积是( )
A.4π
B.6π
C.8π
D.12π
9.如图是从上面看由几个大小相同的小立方块所搭成的几何体得到的形状图,小正方形中的数字表示在该位置的小立方块的个数,则从正面看到的几何体的形状图是( )
A.
B.
C.
D.
10.在一仓库里堆放着若干个大小相同的正方体小货箱,仓库管理员将从三个方向看到的物体的形状图画了出来,如图所示,则这堆正方体小货箱共有( )
A.11个
B.10个
C.9个
D.8个
11.一位画家把边长为1m的7个相同正方体摆成如图的形式,然后把露出的表面涂上颜色,则涂色面积为________m.
12.如图,正方形ABDC的边长为3,以直线AB为轴,将正方形旋转一周,形成一个几何体,则从正面看到的形状图的周长是_______.
13.请写出图中几何体中截面的形状.
①________;②________;③________.
14.已知图为一几何体从不同方向看的图形:
写出这个几何体的名称;
任意画出这个几何体的一种表面展开图;
若长方形的高为厘米,三角形的边长为厘米,求这个几何体的侧面积.
15.用小立方体搭成一个几何体,从正面和上面看到该几何体的形状图如图所示,搭建这样的几何体最多要几个小立方体?最少要几个小立方体?并画出最多和最少时从左面看到的形状图.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
