人教版数学九年级下册第二十六章反比例函数全章教案
文档属性
| 名称 | 人教版数学九年级下册第二十六章反比例函数全章教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 212.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-08 23:21:58 | ||
图片预览


文档简介
第二十六章 反比例函数
26.1 反比例函数
26.1.1 反比例函数
01 教学目标
1.理解并掌握反比例函数的概念.
2.能判断一个给定的函数是否为反比例函数,并会用待定系数法求函数解析式.
3.能根据实际问题中的条件确定反比例函数的解析式,体会函数的模型思想.
02 预习反馈
阅读课本P2~3,理解反比例函数的概念,体会求反比例函数解析式及函数值的过程,完成下列预习内容.
1.小学里我们知道:如果两个变量x,y满足xy=k(k为常数,k≠0),那么x,y就成为反比例关系.例如,速度v、时间t与路程s之间满足vt=s,如果路程s一定,那么速度v与时间t就成反比例关系.
2.一般地,在某一变化过程有两个变量x和y,如果对于变量x的每一个值,变量y都有唯一的值与它对应,我们就称y是x的函数.其中,x是自变量,y是因变量.
3.形如y=(k是常数,k≠0)的函数称为反比例函数,其中x是自变量,y是因变量.自变量x的取值范围是不等于0的一切实数.
03 名校讲坛
例1 下列函数中,哪些是反比例函数?每一个反比例函数相应的k值是多少?
①y=2x+1;②y=;③y=;④y=-;⑤xy=3;
⑥2y=x;⑦xy=-1.
答:③④⑤⑦,k值分别是,-,3,-1.
【点拨】 y=,y=kx-1,xy=k是反比例函数的三种表现形式.其中k是常数,k≠0.
【跟踪训练1】 (《名校课堂》26.1.1反比例函数习题)下列函数关系式中,y是x的反比例函数的是(C)
A.y=3x
B.y=3x+1
C.y=
D.y=3x2
例2 (教材P3例1变式)已知y-2与x+3成反比例,且当x=2时,y=-3.
(1)求y与x的函数解析式;
(2)当y=7时,x的值是多少?
【解答】 (1)设y-2=,因为当x=2时,y=-3,则有-5=.
解得k=-25,∴y=+2.
(2)把y=7代入y=+2,得x=-8.
【跟踪训练2】 已知y是x
的反比例函数,下列给出了x与y的一些值:
x
-1
-
1
y
2
4
-4
-2
(1)写出这个反比例函数的解析式;
(2)根据函数解析式完成上表.
解:设反比例函数的解析式为y=.因为x=-时,y=4.所以有4=,k=-2.所以反比例函数的解析式为y=.
04 巩固训练
1.下列函数:①y=;②y=;③y=-;④y=2x-1中,是反比例函数的有(C)
A.1个
B.2个
C.3个
D.4个
2.如果直角三角形的面积一定,那么下列关于这个直角三角形边的关系的说法中,正确的是(B)
A.两条直角边成正比例
B.两条直角边成反比例
C.一条直角边与斜边成正比例
D.一条直角边与斜边成反比例
3.当m
=6时,y=3xm-7是反比例函数.
4.列出下列问题中的函数关系式,并指出它们是什么函数.
(1)某农场的粮食总产量为1
500
t,则该农场人数y(人)与平均每人占有粮食x(t)的函数关系式;
(2)在加油站,加油机显示器上显示的某一种油的单价为每升4.75元,总价从0元开始随着加油量的变化而变化,则总价y(元)与加油量x(L)的函数关系式;
(3)小明完成100
m赛跑时,时间t(s)与他跑步的平均速度v(m/s)之间的函数关系式.
解:(1)y=,反比例函数.
(2)y=4.75x,正比例函数.
(3)t=,反比例函数.
05 课堂小结
本节课我们学习了什么内容?
26.1.2 反比例函数的图象和性质
第1课时 反比例函数的图象和性质
01 教学目标
会画出反比例函数的图象,并能说出它的性质.
02 预习反馈
阅读课本P4~6,完成下列预习内容.
1.反比例函数的表达式是:y=(k≠0,k为常数).
2.类比一次函数的作图象法,作反比例函数的图象的一般步骤也是:列表、描点、连线.
3.反比例函数图象是双曲线.
4.在反比例函数y=(k≠0,k为常数)中,当k>0时,双曲线位于一、三象限;当k<0时,双曲线位于二、四象限.
03 名校讲坛
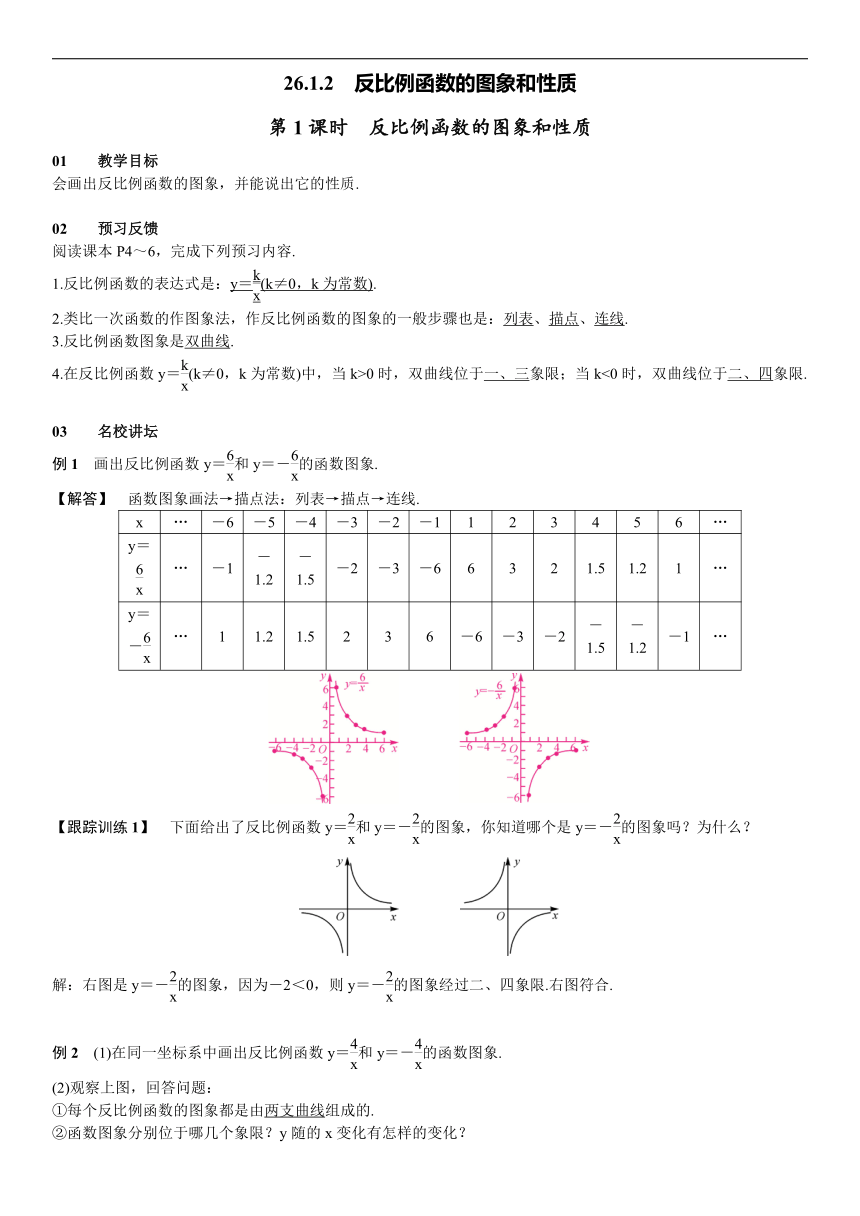
例1 画出反比例函数y=和y=-的函数图象.
【解答】 函数图象画法→描点法:列表→描点→连线.
x
…
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
…
y=
…
-1
-1.2
-1.5
-2
-3
-6
6
3
2
1.5
1.2
1
…
y=-
…
1
1.2
1.5
2
3
6
-6
-3
-2
-1.5
-1.2
-1
…
【跟踪训练1】 下面给出了反比例函数y=和y=-的图象,你知道哪个是y=-的图象吗?为什么?
解:右图是y=-的图象,因为-2<0,则y=-的图象经过二、四象限.右图符合.
例2 (1)在同一坐标系中画出反比例函数y=和y=-的函数图象.
(2)观察上图,回答问题:
①每个反比例函数的图象都是由两支曲线组成的.
②函数图象分别位于哪几个象限?y随的x变化有怎样的变化?
【解答】 (1)列表→描点→连线.
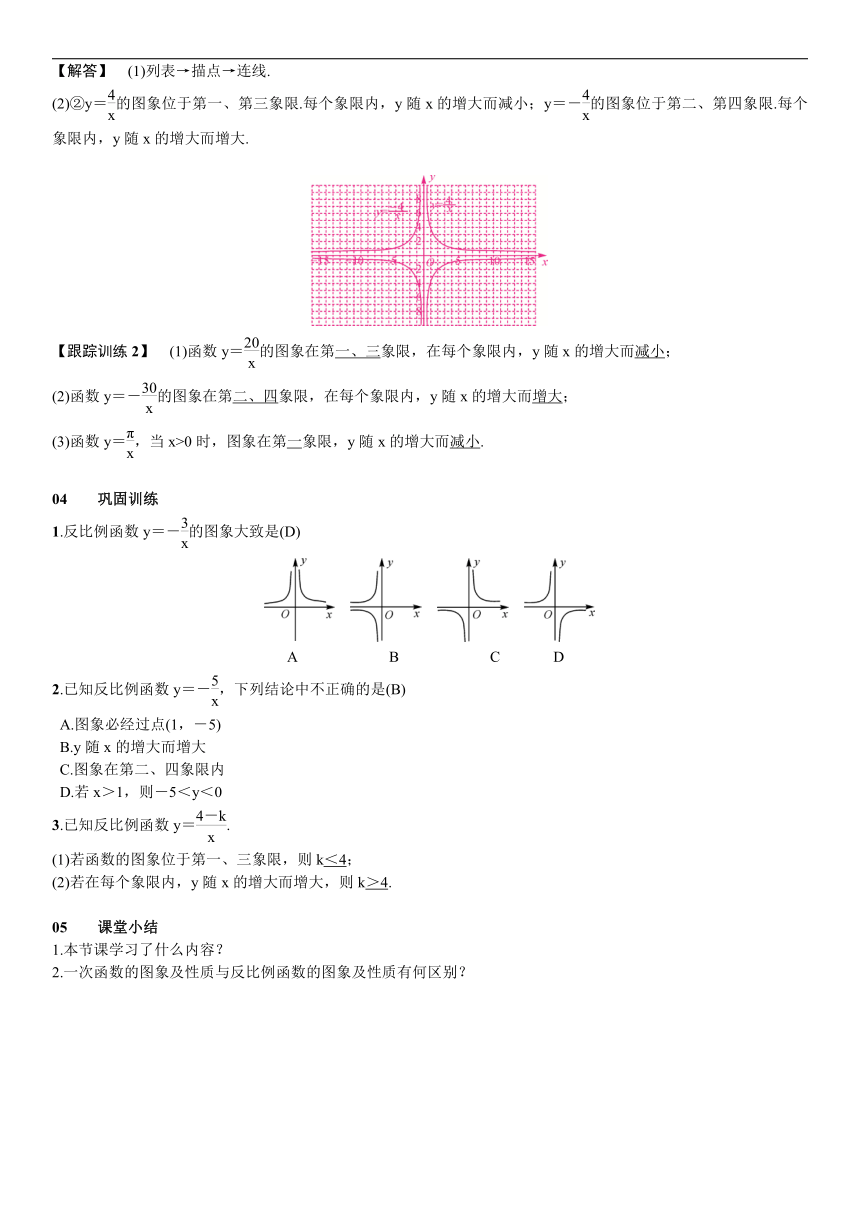
(2)②y=的图象位于第一、第三象限.每个象限内,y随x的增大而减小;y=-的图象位于第二、第四象限.每个象限内,y随x的增大而增大.
【跟踪训练2】 (1)函数y=的图象在第一、三象限,在每个象限内,y随x的增大而减小;
(2)函数y=-的图象在第二、四象限,在每个象限内,y随x的增大而增大;
(3)函数y=,当x>0时,图象在第一象限,y随x的增大而减小.
04 巩固训练
1.反比例函数y=-的图象大致是(D)
A B C
D
2.已知反比例函数y=-,下列结论中不正确的是(B)
A.图象必经过点(1,-5)
B.y随x的增大而增大
C.图象在第二、四象限内
D.若x>1,则-5<y<0
3.已知反比例函数y=.
(1)若函数的图象位于第一、三象限,则k<4;
(2)若在每个象限内,y随x的增大而增大,则k>4.
05 课堂小结
1.本节课学习了什么内容?
2.一次函数的图象及性质与反比例函数的图象及性质有何区别?
第2课时 反比例函数的性质的综合应用
01 教学目标
1.利用反比例函数的知识分析、解决实际问题.
2.渗透数形结合思想,提高学生用函数观点解决问题的能力.
02 预习反馈
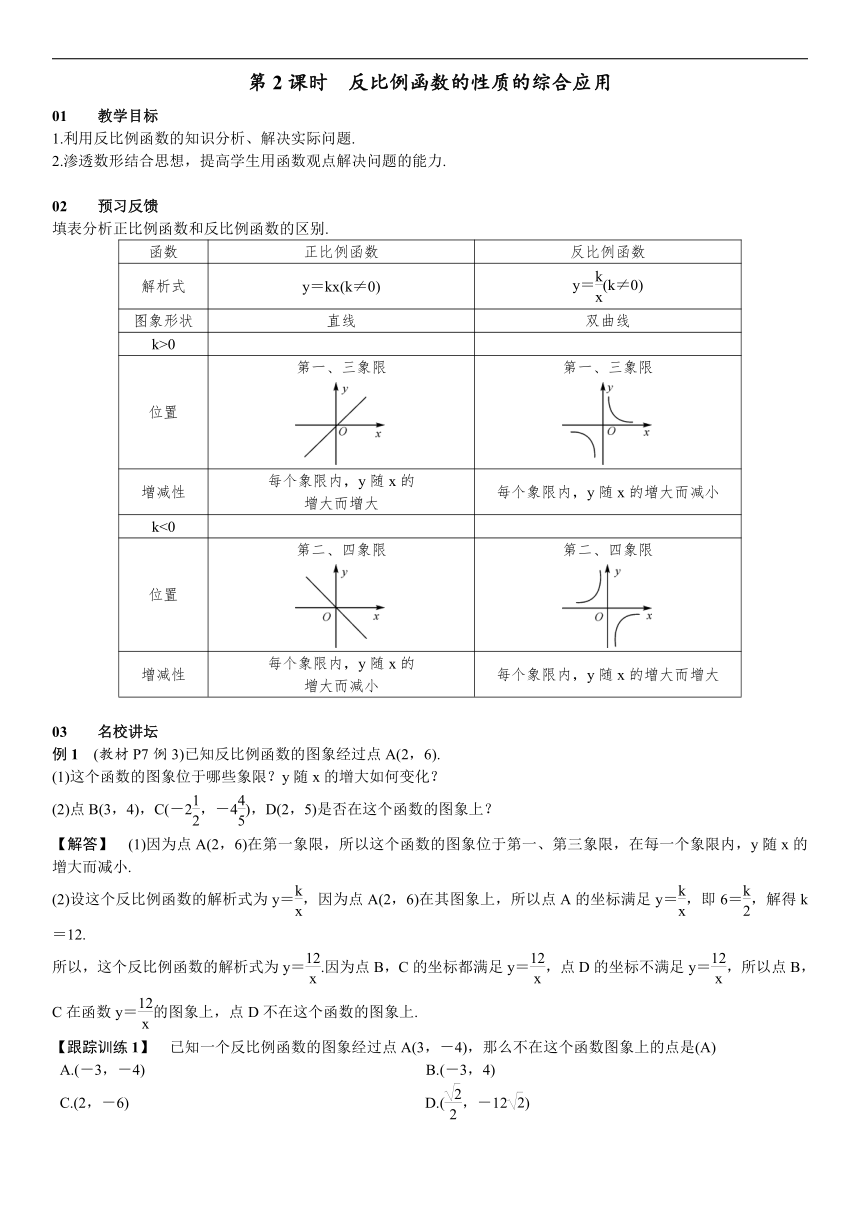
填表分析正比例函数和反比例函数的区别.
函数
正比例函数
反比例函数
解析式
y=kx(k≠0)
y=(k≠0)
图象形状
直线
双曲线
k>0
位置
第一、三象限
第一、三象限
增减性
每个象限内,y随x的
增大而增大
每个象限内,y随x的增大而减小
k<0
位置
第二、四象限
第二、四象限
增减性
每个象限内,y随x的
增大而减小
每个象限内,y随x的增大而增大
03 名校讲坛
例1 (教材P7例3)已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象位于哪些象限?y随x的增大如何变化?
(2)点B(3,4),C(-2,-4),D(2,5)是否在这个函数的图象上?
【解答】 (1)因为点A(2,6)在第一象限,所以这个函数的图象位于第一、第三象限,在每一个象限内,y随x的增大而减小.
(2)设这个反比例函数的解析式为y=,因为点A(2,6)在其图象上,所以点A的坐标满足y=,即6=,解得k=12.
所以,这个反比例函数的解析式为y=.因为点B,C的坐标都满足y=,点D的坐标不满足y=,所以点B,C在函数y=的图象上,点D不在这个函数的图象上.
【跟踪训练1】 已知一个反比例函数的图象经过点A(3,-4),那么不在这个函数图象上的点是(A)
A.(-3,-4)
B.(-3,4)
C.(2,-6)
D.(,-12)
例2 (教材补充例题)如图,已知反比例函数y=(k≠0)的图象经过点A(-2,m),过点A作AB⊥x轴于点B,且△AOB的面积为4.
(1)求k和m的值;
(2)设(x,y)是该反比例函数图象上一点,当1≤x≤4时,求函数值y的取值范围.
【解答】 (1)∵△AOB的面积为4,
∴(-xA)·yA=4,
即可得,k=xA·yA=-8.
令x=-2,得m=4.
(2)当1≤x≤4时,y随x的增大而增大,
令x=1,得y=-8;
令x=4,得y=-2.
所以-8≤y≤-2即为所求.
【跟踪训练2】
(《名校课堂》26.1.2第1课时习题)如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数y=的图象于点B,AB=.
(1)求反比例函数的解析式;
(2)若P(x1,y1),Q(x2,y2)是该反比例函数图象上的两点,且x1y2,指出点P,Q各位于哪个象限?并简要说明理由.
解:(1)由题意,得A(-2,0),AB=,AB∥y轴,
∴B(-2,).
∵反比例函数y=的图象经过点B,
∴k=-3.
∴反比例函数的解析式为y=-.
(2)点P在第二象限,点Q在第四象限.理由:
∵k<0,∴在每一象限内,y随x的增大而增大.
又∵x1<x2,y1>y2,
∴x1<0<x2.
∴点P在第二象限,点Q在第四象限.
04 巩固训练
1.反比例函数y=的图象经过点(2,5),若点(1,n)在反比例函数图象上,则n等于(A)
A.10
B.5
C.2
D.-6
2.下列各点在反比例函数y=-的图象上的是(B)
A.(-,-)
B.(-,)
C.(,)
D.(,)
3.在反比例函数y=-的图象上有三点(x1,y1),(x2,y2),(x3,y3),x1>x2>0>x3,则下列各式中正确的是(A)
A.y3>y1>y2
B.y3>y2>y1
C.y1>y2>y3
D.y1>y3>y2
【点拨】 因为k<0,所以图象在二、四象限;在每个象限内,y随x的增大而增大.又x1>x2>0>x3,所以y1,y2在第四象限且0>y1>y2;y3在第二象限且y3>0,所以y3>y1>y2.
4.反比例函数y=的图象经过点(2,-1),则k的值为-2.
5.如图,点P是反比例函数y=图象上的一点,PD⊥x轴于点D.则△POD的面积为1.
【点拨】 因为点P在图象上,所以n=,即mn=2;故S△POD=OD·PD=mn=1.
6.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的关系式是y=-.
【点拨】 设函数为y=,而P在图象上,所以k=mn,又阴影部分面积是|mn|=3,函数图象在第二象限,所以k<0,即k=-3,所以函数关系式为y=-.
05 课堂小结
本节课我们学习了哪些内容?
26.2 实际问题与反比例函数
01 教学目标
1.运用反比例函数解决实际问题.
2.学会把实际问题转化为反比例函数问题.
02 预习反馈
阅读课本P12~15,完成下列预习内容.
1.矩形面积是40
m2,设它的一边长为x(m),则矩形的另一边长y(m)与x的函数关系是(C)
A.y=20-x
B.y=40x
C.y=
D.y=
2.一司机驾驶汽车从甲地去乙地,他以平均80千米/小时的速度用了4个小时到达乙地,当他按原路匀速返回时.汽车的速度v千米/小时与时间t小时的函数关系是(B)
A.v=320t
B.v=
C.v=20t
D.v=
3.某厂现有300吨煤,这些煤能烧的天数y与平均每天烧的吨数x之间的函数关系是(A)
A.y=(x>0)
B.y=(x≥0)
C.y=300x(x≥0)
D.y=300x(x>0)
03 名校讲坛
例1 (教材P12例1)市煤气公司要在地下修建一个容积为104
m3的圆柱形煤气储存室.
(1)储存室的底面积S(单位:m2)与其深度d(单位:m)有怎样的函数关系?
(2)公司决定把储存室的底面积S定为500
m2,施工队施工时应该向下掘进多深?
(3)当施工队按(2)中的计划掘进到地下15
m时,公司临时改变计划,把储存室的深改为15
m,相应地,储存室的底面积应改为多少(结果保留小数点后两位)?
【解答】 (1)根据圆柱体的体积公式,有S·d=104,变形,得S=,即储存室的底面积S是其深度d的反比例函数.
(2)把S=500代入S=,得d=20(m).
答:如果把储存室的底面积定为500
m2,施工时应向地下掘进20
m深.
(3)根据题意,把d=15代入S=,得S=≈666.67(m2).
答:当储存室的深度为15
m时,储存室的底面积应改为666.67
m2才能满足需要.
【跟踪训练1】 (《名校课堂》26.2习题)学校准备在校园内修建一个矩形的绿化带,矩形的面积为定值,它的一边y(m)与另一边x(m)之间的函数关系如图所示.
(1)绿化带面积是多少?你能写出这一函数解析式吗?
(2)完成下表,并回答问题:如果该绿化带的长不得超过40
m,那么它的宽应控制在什么范围内?
x(m)
10
20
30
40
y(m)
40
20
10
解:(1)绿化带面积为10×40=400(m2).
设该反比例函数的解析式为y=.
∵图象经过点A(40,10),把x=40,y=10代入,得10=,解得k=400.
∴反比例函数的解析式为y=.
(2)如表.
从图中可以看出,如果长不超过40
m,那么它的宽应大于等于10
m.
例2 (教材补充例题)如图所示是某一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
(1)请你根据图象提供的信息求出此蓄水池的蓄水量;
(2)写出此函数的解析式;
(3)如果要6
h排完水池中的水,那么每小时的排水量应该是多少?
【解答】 (1)因为当蓄水总量一定时,每小时的排水量与排水所用时间成反比例,所以根据图象提供的信息可知,此蓄水池的蓄水量为:4
000×12=48
000(m3).
(2)因为此函数为反比例函数,所以解析式为:V=.
(3)如果要6
h排完水池中的水,那么每小时的排水量为:V==8
000(m3).
【跟踪训练2】
(《名校课堂》26.2习题)将油箱注满k升油后,轿车可行驶的总路程s(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系s=(k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.
(1)求该轿车可行驶的总路程s与平均耗油量a之间的函数解析式;
(2)当平均耗油量为0.08升/千米时,该轿车可以行驶多少千米?
解:(1)由题意,得a=0.1时,s=700,
代入反比例函数关系s=中,解得k=sa=70.
∴函数解析式为s=.
(2)当a=0.08时,s==875.
答:该轿车可以行驶875千米.
例3 (教材P15例4)一个用电器的电阻是可调节的,其范围为110~220
Ω.已知电压为220
v,这个用电器的电路图如图所示.
(1)功率P与电阻R有怎样的函数关系?
(2)这个用电器功率范围是多少?
【解答】 (1)根据电学知识,当U=220时,得P=.①
(2)根据反比例函数的性质可知,电阻越大,功率越小,把电阻的最小值R=110代入①式,得到功率的最大值P==440(W);
把电阻的最大值R=220代入①式,得到功率的最小值P==220(W).
答:用电器功率的范围为220~440
W.
【跟踪训练3】 某气球内充满了一定量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求这一函数的解析式;
(2)当气体体积为1
m3时,气压是多少?
(3)当气球内的气压大于140
kPa时,气球将爆炸,为了安全起见,气体的体积应不小于多少?(精确到0.01
m3)
解:(1)设p=,
由题意,知120=,所以k=96.
故p=.
(2)当V=1
m3时,p==96(kPa).
(3)当p=140
kPa时,V=≈0.69(m3).
答:为了安全起见,气体的体积应不少于0.69
m3.
04 巩固训练
1.某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图表示的是该电路中电流I与电阻R之间函数关系的图象,则用电阻R表示电流I的函数解析式为(C)
A.I=
B.I=
C.I=
D.I=-
2.某商场出售一批进价为2元的贺卡,在市场营销中发现此贺卡的日销售单价x(元)与日销售量y(个)之间有如下关系:
日销售单价x(元)
…
3
4
5
6
…
日销售量y(个)
…
20
15
12
10
…
则y与x之间的函数关系式为y=.
3.近视眼镜的度数y(度)与焦距x(m)成反比例,已知400度近视眼镜镜片的焦距为0.25
m.
(1)试求眼镜度数y与镜片焦距x之间的函数关系式;
(2)求1
000度近视眼镜镜片的焦距.
解:(1)设y=,
把x=0.25,y=400代入,得400=,
所以k=400×0.25=100,即所求的函数关系式为y=.
(2)当y=1
000时,1
000=,解得x=0.1.
答:1
000度近视眼镜镜片的焦距为0.1
m.
4.制作一种产品,需先将材料加热到达60
℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图所示).已知该材料在操作加工前的温度为15
℃,加热5分钟后温度达到60
℃.
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15
℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
解:(1)当0≤x≤5时,设y=k1x+b,
由得
∴y=9x+15.
当x≥5时,设y=,
由x=5时,y=60,知k2=300.∴y=.
(2)当y=15时,由15=,得x=20.
答:从开始加热到停止操作,共经历了20分钟.
05 课堂小结
本节课我们学习了什么内容?
26.1 反比例函数
26.1.1 反比例函数
01 教学目标
1.理解并掌握反比例函数的概念.
2.能判断一个给定的函数是否为反比例函数,并会用待定系数法求函数解析式.
3.能根据实际问题中的条件确定反比例函数的解析式,体会函数的模型思想.
02 预习反馈
阅读课本P2~3,理解反比例函数的概念,体会求反比例函数解析式及函数值的过程,完成下列预习内容.
1.小学里我们知道:如果两个变量x,y满足xy=k(k为常数,k≠0),那么x,y就成为反比例关系.例如,速度v、时间t与路程s之间满足vt=s,如果路程s一定,那么速度v与时间t就成反比例关系.
2.一般地,在某一变化过程有两个变量x和y,如果对于变量x的每一个值,变量y都有唯一的值与它对应,我们就称y是x的函数.其中,x是自变量,y是因变量.
3.形如y=(k是常数,k≠0)的函数称为反比例函数,其中x是自变量,y是因变量.自变量x的取值范围是不等于0的一切实数.
03 名校讲坛
例1 下列函数中,哪些是反比例函数?每一个反比例函数相应的k值是多少?
①y=2x+1;②y=;③y=;④y=-;⑤xy=3;
⑥2y=x;⑦xy=-1.
答:③④⑤⑦,k值分别是,-,3,-1.
【点拨】 y=,y=kx-1,xy=k是反比例函数的三种表现形式.其中k是常数,k≠0.
【跟踪训练1】 (《名校课堂》26.1.1反比例函数习题)下列函数关系式中,y是x的反比例函数的是(C)
A.y=3x
B.y=3x+1
C.y=
D.y=3x2
例2 (教材P3例1变式)已知y-2与x+3成反比例,且当x=2时,y=-3.
(1)求y与x的函数解析式;
(2)当y=7时,x的值是多少?
【解答】 (1)设y-2=,因为当x=2时,y=-3,则有-5=.
解得k=-25,∴y=+2.
(2)把y=7代入y=+2,得x=-8.
【跟踪训练2】 已知y是x
的反比例函数,下列给出了x与y的一些值:
x
-1
-
1
y
2
4
-4
-2
(1)写出这个反比例函数的解析式;
(2)根据函数解析式完成上表.
解:设反比例函数的解析式为y=.因为x=-时,y=4.所以有4=,k=-2.所以反比例函数的解析式为y=.
04 巩固训练
1.下列函数:①y=;②y=;③y=-;④y=2x-1中,是反比例函数的有(C)
A.1个
B.2个
C.3个
D.4个
2.如果直角三角形的面积一定,那么下列关于这个直角三角形边的关系的说法中,正确的是(B)
A.两条直角边成正比例
B.两条直角边成反比例
C.一条直角边与斜边成正比例
D.一条直角边与斜边成反比例
3.当m
=6时,y=3xm-7是反比例函数.
4.列出下列问题中的函数关系式,并指出它们是什么函数.
(1)某农场的粮食总产量为1
500
t,则该农场人数y(人)与平均每人占有粮食x(t)的函数关系式;
(2)在加油站,加油机显示器上显示的某一种油的单价为每升4.75元,总价从0元开始随着加油量的变化而变化,则总价y(元)与加油量x(L)的函数关系式;
(3)小明完成100
m赛跑时,时间t(s)与他跑步的平均速度v(m/s)之间的函数关系式.
解:(1)y=,反比例函数.
(2)y=4.75x,正比例函数.
(3)t=,反比例函数.
05 课堂小结
本节课我们学习了什么内容?
26.1.2 反比例函数的图象和性质
第1课时 反比例函数的图象和性质
01 教学目标
会画出反比例函数的图象,并能说出它的性质.
02 预习反馈
阅读课本P4~6,完成下列预习内容.
1.反比例函数的表达式是:y=(k≠0,k为常数).
2.类比一次函数的作图象法,作反比例函数的图象的一般步骤也是:列表、描点、连线.
3.反比例函数图象是双曲线.
4.在反比例函数y=(k≠0,k为常数)中,当k>0时,双曲线位于一、三象限;当k<0时,双曲线位于二、四象限.
03 名校讲坛
例1 画出反比例函数y=和y=-的函数图象.
【解答】 函数图象画法→描点法:列表→描点→连线.
x
…
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
…
y=
…
-1
-1.2
-1.5
-2
-3
-6
6
3
2
1.5
1.2
1
…
y=-
…
1
1.2
1.5
2
3
6
-6
-3
-2
-1.5
-1.2
-1
…
【跟踪训练1】 下面给出了反比例函数y=和y=-的图象,你知道哪个是y=-的图象吗?为什么?
解:右图是y=-的图象,因为-2<0,则y=-的图象经过二、四象限.右图符合.
例2 (1)在同一坐标系中画出反比例函数y=和y=-的函数图象.
(2)观察上图,回答问题:
①每个反比例函数的图象都是由两支曲线组成的.
②函数图象分别位于哪几个象限?y随的x变化有怎样的变化?
【解答】 (1)列表→描点→连线.
(2)②y=的图象位于第一、第三象限.每个象限内,y随x的增大而减小;y=-的图象位于第二、第四象限.每个象限内,y随x的增大而增大.
【跟踪训练2】 (1)函数y=的图象在第一、三象限,在每个象限内,y随x的增大而减小;
(2)函数y=-的图象在第二、四象限,在每个象限内,y随x的增大而增大;
(3)函数y=,当x>0时,图象在第一象限,y随x的增大而减小.
04 巩固训练
1.反比例函数y=-的图象大致是(D)
A B C
D
2.已知反比例函数y=-,下列结论中不正确的是(B)
A.图象必经过点(1,-5)
B.y随x的增大而增大
C.图象在第二、四象限内
D.若x>1,则-5<y<0
3.已知反比例函数y=.
(1)若函数的图象位于第一、三象限,则k<4;
(2)若在每个象限内,y随x的增大而增大,则k>4.
05 课堂小结
1.本节课学习了什么内容?
2.一次函数的图象及性质与反比例函数的图象及性质有何区别?
第2课时 反比例函数的性质的综合应用
01 教学目标
1.利用反比例函数的知识分析、解决实际问题.
2.渗透数形结合思想,提高学生用函数观点解决问题的能力.
02 预习反馈
填表分析正比例函数和反比例函数的区别.
函数
正比例函数
反比例函数
解析式
y=kx(k≠0)
y=(k≠0)
图象形状
直线
双曲线
k>0
位置
第一、三象限
第一、三象限
增减性
每个象限内,y随x的
增大而增大
每个象限内,y随x的增大而减小
k<0
位置
第二、四象限
第二、四象限
增减性
每个象限内,y随x的
增大而减小
每个象限内,y随x的增大而增大
03 名校讲坛
例1 (教材P7例3)已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象位于哪些象限?y随x的增大如何变化?
(2)点B(3,4),C(-2,-4),D(2,5)是否在这个函数的图象上?
【解答】 (1)因为点A(2,6)在第一象限,所以这个函数的图象位于第一、第三象限,在每一个象限内,y随x的增大而减小.
(2)设这个反比例函数的解析式为y=,因为点A(2,6)在其图象上,所以点A的坐标满足y=,即6=,解得k=12.
所以,这个反比例函数的解析式为y=.因为点B,C的坐标都满足y=,点D的坐标不满足y=,所以点B,C在函数y=的图象上,点D不在这个函数的图象上.
【跟踪训练1】 已知一个反比例函数的图象经过点A(3,-4),那么不在这个函数图象上的点是(A)
A.(-3,-4)
B.(-3,4)
C.(2,-6)
D.(,-12)
例2 (教材补充例题)如图,已知反比例函数y=(k≠0)的图象经过点A(-2,m),过点A作AB⊥x轴于点B,且△AOB的面积为4.
(1)求k和m的值;
(2)设(x,y)是该反比例函数图象上一点,当1≤x≤4时,求函数值y的取值范围.
【解答】 (1)∵△AOB的面积为4,
∴(-xA)·yA=4,
即可得,k=xA·yA=-8.
令x=-2,得m=4.
(2)当1≤x≤4时,y随x的增大而增大,
令x=1,得y=-8;
令x=4,得y=-2.
所以-8≤y≤-2即为所求.
【跟踪训练2】
(《名校课堂》26.1.2第1课时习题)如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数y=的图象于点B,AB=.
(1)求反比例函数的解析式;
(2)若P(x1,y1),Q(x2,y2)是该反比例函数图象上的两点,且x1
解:(1)由题意,得A(-2,0),AB=,AB∥y轴,
∴B(-2,).
∵反比例函数y=的图象经过点B,
∴k=-3.
∴反比例函数的解析式为y=-.
(2)点P在第二象限,点Q在第四象限.理由:
∵k<0,∴在每一象限内,y随x的增大而增大.
又∵x1<x2,y1>y2,
∴x1<0<x2.
∴点P在第二象限,点Q在第四象限.
04 巩固训练
1.反比例函数y=的图象经过点(2,5),若点(1,n)在反比例函数图象上,则n等于(A)
A.10
B.5
C.2
D.-6
2.下列各点在反比例函数y=-的图象上的是(B)
A.(-,-)
B.(-,)
C.(,)
D.(,)
3.在反比例函数y=-的图象上有三点(x1,y1),(x2,y2),(x3,y3),x1>x2>0>x3,则下列各式中正确的是(A)
A.y3>y1>y2
B.y3>y2>y1
C.y1>y2>y3
D.y1>y3>y2
【点拨】 因为k<0,所以图象在二、四象限;在每个象限内,y随x的增大而增大.又x1>x2>0>x3,所以y1,y2在第四象限且0>y1>y2;y3在第二象限且y3>0,所以y3>y1>y2.
4.反比例函数y=的图象经过点(2,-1),则k的值为-2.
5.如图,点P是反比例函数y=图象上的一点,PD⊥x轴于点D.则△POD的面积为1.
【点拨】 因为点P在图象上,所以n=,即mn=2;故S△POD=OD·PD=mn=1.
6.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的关系式是y=-.
【点拨】 设函数为y=,而P在图象上,所以k=mn,又阴影部分面积是|mn|=3,函数图象在第二象限,所以k<0,即k=-3,所以函数关系式为y=-.
05 课堂小结
本节课我们学习了哪些内容?
26.2 实际问题与反比例函数
01 教学目标
1.运用反比例函数解决实际问题.
2.学会把实际问题转化为反比例函数问题.
02 预习反馈
阅读课本P12~15,完成下列预习内容.
1.矩形面积是40
m2,设它的一边长为x(m),则矩形的另一边长y(m)与x的函数关系是(C)
A.y=20-x
B.y=40x
C.y=
D.y=
2.一司机驾驶汽车从甲地去乙地,他以平均80千米/小时的速度用了4个小时到达乙地,当他按原路匀速返回时.汽车的速度v千米/小时与时间t小时的函数关系是(B)
A.v=320t
B.v=
C.v=20t
D.v=
3.某厂现有300吨煤,这些煤能烧的天数y与平均每天烧的吨数x之间的函数关系是(A)
A.y=(x>0)
B.y=(x≥0)
C.y=300x(x≥0)
D.y=300x(x>0)
03 名校讲坛
例1 (教材P12例1)市煤气公司要在地下修建一个容积为104
m3的圆柱形煤气储存室.
(1)储存室的底面积S(单位:m2)与其深度d(单位:m)有怎样的函数关系?
(2)公司决定把储存室的底面积S定为500
m2,施工队施工时应该向下掘进多深?
(3)当施工队按(2)中的计划掘进到地下15
m时,公司临时改变计划,把储存室的深改为15
m,相应地,储存室的底面积应改为多少(结果保留小数点后两位)?
【解答】 (1)根据圆柱体的体积公式,有S·d=104,变形,得S=,即储存室的底面积S是其深度d的反比例函数.
(2)把S=500代入S=,得d=20(m).
答:如果把储存室的底面积定为500
m2,施工时应向地下掘进20
m深.
(3)根据题意,把d=15代入S=,得S=≈666.67(m2).
答:当储存室的深度为15
m时,储存室的底面积应改为666.67
m2才能满足需要.
【跟踪训练1】 (《名校课堂》26.2习题)学校准备在校园内修建一个矩形的绿化带,矩形的面积为定值,它的一边y(m)与另一边x(m)之间的函数关系如图所示.
(1)绿化带面积是多少?你能写出这一函数解析式吗?
(2)完成下表,并回答问题:如果该绿化带的长不得超过40
m,那么它的宽应控制在什么范围内?
x(m)
10
20
30
40
y(m)
40
20
10
解:(1)绿化带面积为10×40=400(m2).
设该反比例函数的解析式为y=.
∵图象经过点A(40,10),把x=40,y=10代入,得10=,解得k=400.
∴反比例函数的解析式为y=.
(2)如表.
从图中可以看出,如果长不超过40
m,那么它的宽应大于等于10
m.
例2 (教材补充例题)如图所示是某一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
(1)请你根据图象提供的信息求出此蓄水池的蓄水量;
(2)写出此函数的解析式;
(3)如果要6
h排完水池中的水,那么每小时的排水量应该是多少?
【解答】 (1)因为当蓄水总量一定时,每小时的排水量与排水所用时间成反比例,所以根据图象提供的信息可知,此蓄水池的蓄水量为:4
000×12=48
000(m3).
(2)因为此函数为反比例函数,所以解析式为:V=.
(3)如果要6
h排完水池中的水,那么每小时的排水量为:V==8
000(m3).
【跟踪训练2】
(《名校课堂》26.2习题)将油箱注满k升油后,轿车可行驶的总路程s(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系s=(k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.
(1)求该轿车可行驶的总路程s与平均耗油量a之间的函数解析式;
(2)当平均耗油量为0.08升/千米时,该轿车可以行驶多少千米?
解:(1)由题意,得a=0.1时,s=700,
代入反比例函数关系s=中,解得k=sa=70.
∴函数解析式为s=.
(2)当a=0.08时,s==875.
答:该轿车可以行驶875千米.
例3 (教材P15例4)一个用电器的电阻是可调节的,其范围为110~220
Ω.已知电压为220
v,这个用电器的电路图如图所示.
(1)功率P与电阻R有怎样的函数关系?
(2)这个用电器功率范围是多少?
【解答】 (1)根据电学知识,当U=220时,得P=.①
(2)根据反比例函数的性质可知,电阻越大,功率越小,把电阻的最小值R=110代入①式,得到功率的最大值P==440(W);
把电阻的最大值R=220代入①式,得到功率的最小值P==220(W).
答:用电器功率的范围为220~440
W.
【跟踪训练3】 某气球内充满了一定量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求这一函数的解析式;
(2)当气体体积为1
m3时,气压是多少?
(3)当气球内的气压大于140
kPa时,气球将爆炸,为了安全起见,气体的体积应不小于多少?(精确到0.01
m3)
解:(1)设p=,
由题意,知120=,所以k=96.
故p=.
(2)当V=1
m3时,p==96(kPa).
(3)当p=140
kPa时,V=≈0.69(m3).
答:为了安全起见,气体的体积应不少于0.69
m3.
04 巩固训练
1.某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图表示的是该电路中电流I与电阻R之间函数关系的图象,则用电阻R表示电流I的函数解析式为(C)
A.I=
B.I=
C.I=
D.I=-
2.某商场出售一批进价为2元的贺卡,在市场营销中发现此贺卡的日销售单价x(元)与日销售量y(个)之间有如下关系:
日销售单价x(元)
…
3
4
5
6
…
日销售量y(个)
…
20
15
12
10
…
则y与x之间的函数关系式为y=.
3.近视眼镜的度数y(度)与焦距x(m)成反比例,已知400度近视眼镜镜片的焦距为0.25
m.
(1)试求眼镜度数y与镜片焦距x之间的函数关系式;
(2)求1
000度近视眼镜镜片的焦距.
解:(1)设y=,
把x=0.25,y=400代入,得400=,
所以k=400×0.25=100,即所求的函数关系式为y=.
(2)当y=1
000时,1
000=,解得x=0.1.
答:1
000度近视眼镜镜片的焦距为0.1
m.
4.制作一种产品,需先将材料加热到达60
℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图所示).已知该材料在操作加工前的温度为15
℃,加热5分钟后温度达到60
℃.
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15
℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
解:(1)当0≤x≤5时,设y=k1x+b,
由得
∴y=9x+15.
当x≥5时,设y=,
由x=5时,y=60,知k2=300.∴y=.
(2)当y=15时,由15=,得x=20.
答:从开始加热到停止操作,共经历了20分钟.
05 课堂小结
本节课我们学习了什么内容?
