2020-2021学年人教版八年级下册数学 17.1勾股定理 同步练习(Word版 含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学 17.1勾股定理 同步练习(Word版 含答案) | 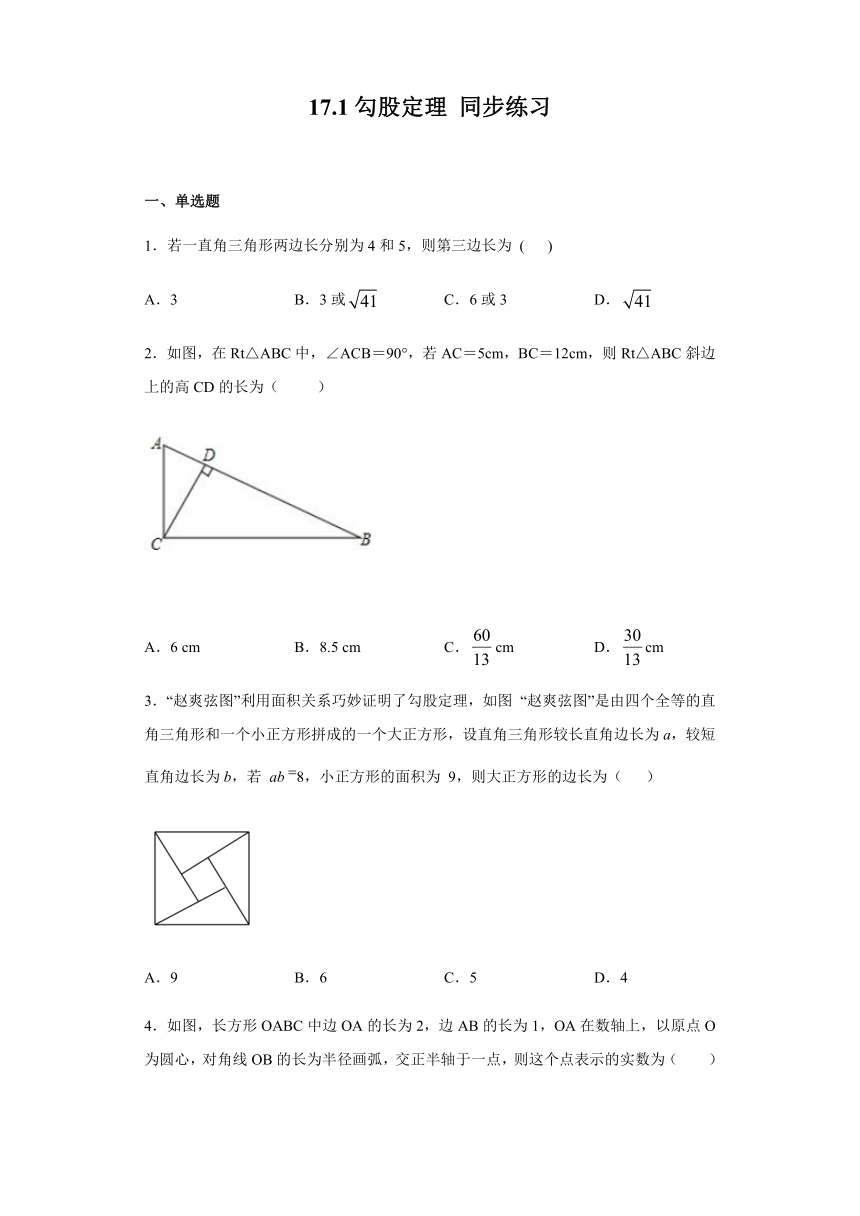 | |
| 格式 | docx | ||
| 文件大小 | 218.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-07 22:49:13 | ||
图片预览


文档简介
17.1勾股定理
同步练习
一、单选题
1.若一直角三角形两边长分别为4和5,则第三边长为
(
)
A.3
B.3或
C.6或3
D.
2.如图,在Rt△ABC中,∠ACB=90°,若AC=5cm,BC=12cm,则Rt△ABC斜边上的高CD的长为(
)
A.6
cm
B.8.5
cm
C.cm
D.cm
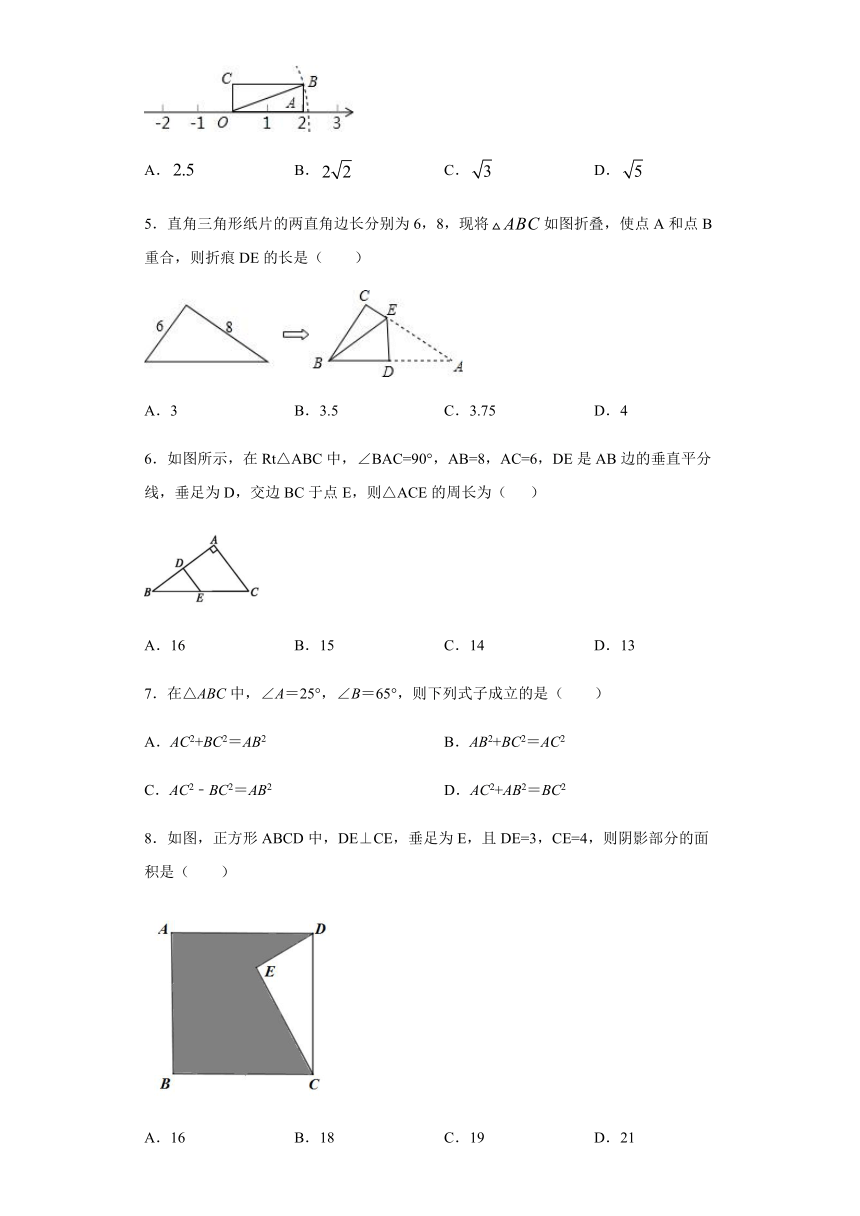
3.“赵爽弦图”利用面积关系巧妙证明了勾股定理,如图
“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若
ab
8,小正方形的面积为
9,则大正方形的边长为(
)
A.9
B.6
C.5
D.4
4.如图,长方形OABC中边OA的长为2,边AB的长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数为(
)
A.
B.
C.
D.
5.直角三角形纸片的两直角边长分别为6,8,现将如图折叠,使点A和点B重合,则折痕DE的长是(
)
A.3
B.3.5
C.3.75
D.4
6.如图所示,在Rt△ABC中,∠BAC=90°,AB=8,AC=6,DE是AB边的垂直平分线,垂足为D,交边BC于点E,则△ACE的周长为(
)
A.16
B.15
C.14
D.13
7.在△ABC中,∠A=25°,∠B=65°,则下列式子成立的是( )
A.AC2+BC2=AB2
B.AB2+BC2=AC2
C.AC2﹣BC2=AB2
D.AC2+AB2=BC2
8.如图,正方形ABCD中,DE⊥CE,垂足为E,且DE=3,CE=4,则阴影部分的面积是( )
A.16
B.18
C.19
D.21
9.如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则△BCN的面积是( )
A.
B.
C.
D.
10.勾股定理历史悠久,三国时期的赵爽证明了勾股定理,后人借助“赵爽弦图”,用三个正方形证明勾股定理,如图所示,B,C,M,G在同一条直线上,四边形ABCD,四边形CEFG,四边形AMFN都为正方形,若五边形ABGFN的面积为34,CM=2,则△ABM的面积为(
)
A.10
B.
C.5
D.4
二、填空题
11.如图,在中,是的平分线,若,则______.
12.边长为6的等边三角形的面积是__________.
13.如图,四边形ABCD中,AC⊥BD,垂足为O,若AB=3,BC=5,CD=6,则AD=_______.
14.如图中的螺旋由一系列直角三角形组成,则线段的长度为__________.
15.如图,点E为矩形的边上一点,以为折痕将向上折叠,点B恰好落在边上的点F处,若,,则的长是__________.
三、解答题
16.如图,在△ABC中,∠C=90?,∠A=30?,BD是∠ABC的平分线,BD=6cm,求AB的长.
17.如图,在和中,AB为斜边,AC=BD,BC、AD相交于点E
(1)请说明AE=BE的理由;
(2)若∠AEC=45°,AC=1,求CB的长.
18.如图,在三角形纸片中,在上取一点,以为折痕,使的一部分与重合,点与延长线上的点重合.
(1)的长=________.
(2)求的长
参考答案
1.B
2.C
3.C
4.D
5.C
6.A
7.A
8.C
9.B
10.C
11.
12.
13.
14.
15.10
16.
17.(1)证明略;(2)
18.(1)12;(2)
同步练习
一、单选题
1.若一直角三角形两边长分别为4和5,则第三边长为
(
)
A.3
B.3或
C.6或3
D.
2.如图,在Rt△ABC中,∠ACB=90°,若AC=5cm,BC=12cm,则Rt△ABC斜边上的高CD的长为(
)
A.6
cm
B.8.5
cm
C.cm
D.cm
3.“赵爽弦图”利用面积关系巧妙证明了勾股定理,如图
“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若
ab
8,小正方形的面积为
9,则大正方形的边长为(
)
A.9
B.6
C.5
D.4
4.如图,长方形OABC中边OA的长为2,边AB的长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数为(
)
A.
B.
C.
D.
5.直角三角形纸片的两直角边长分别为6,8,现将如图折叠,使点A和点B重合,则折痕DE的长是(
)
A.3
B.3.5
C.3.75
D.4
6.如图所示,在Rt△ABC中,∠BAC=90°,AB=8,AC=6,DE是AB边的垂直平分线,垂足为D,交边BC于点E,则△ACE的周长为(
)
A.16
B.15
C.14
D.13
7.在△ABC中,∠A=25°,∠B=65°,则下列式子成立的是( )
A.AC2+BC2=AB2
B.AB2+BC2=AC2
C.AC2﹣BC2=AB2
D.AC2+AB2=BC2
8.如图,正方形ABCD中,DE⊥CE,垂足为E,且DE=3,CE=4,则阴影部分的面积是( )
A.16
B.18
C.19
D.21
9.如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则△BCN的面积是( )
A.
B.
C.
D.
10.勾股定理历史悠久,三国时期的赵爽证明了勾股定理,后人借助“赵爽弦图”,用三个正方形证明勾股定理,如图所示,B,C,M,G在同一条直线上,四边形ABCD,四边形CEFG,四边形AMFN都为正方形,若五边形ABGFN的面积为34,CM=2,则△ABM的面积为(
)
A.10
B.
C.5
D.4
二、填空题
11.如图,在中,是的平分线,若,则______.
12.边长为6的等边三角形的面积是__________.
13.如图,四边形ABCD中,AC⊥BD,垂足为O,若AB=3,BC=5,CD=6,则AD=_______.
14.如图中的螺旋由一系列直角三角形组成,则线段的长度为__________.
15.如图,点E为矩形的边上一点,以为折痕将向上折叠,点B恰好落在边上的点F处,若,,则的长是__________.
三、解答题
16.如图,在△ABC中,∠C=90?,∠A=30?,BD是∠ABC的平分线,BD=6cm,求AB的长.
17.如图,在和中,AB为斜边,AC=BD,BC、AD相交于点E
(1)请说明AE=BE的理由;
(2)若∠AEC=45°,AC=1,求CB的长.
18.如图,在三角形纸片中,在上取一点,以为折痕,使的一部分与重合,点与延长线上的点重合.
(1)的长=________.
(2)求的长
参考答案
1.B
2.C
3.C
4.D
5.C
6.A
7.A
8.C
9.B
10.C
11.
12.
13.
14.
15.10
16.
17.(1)证明略;(2)
18.(1)12;(2)
