人教版八年级下册19.2.2《一次函数》 用待定系数法求一次函数解析式 同步习题(word含答案)
文档属性
| 名称 | 人教版八年级下册19.2.2《一次函数》 用待定系数法求一次函数解析式 同步习题(word含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 844.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-08 00:00:00 | ||
图片预览



文档简介
19.2.2 《一次函数》-用待定系数法求一次函数解析式 同步习题(1)
一、 选择题
1. 一次函数的图象经过点,每当x增加个单位时,增加个单位,则此函数表达式是(? ? ? ? )
A. B. C. D.
2. 若一次函数的图象经过,两点,则的值为(????????)
A. B. C. D.
3. 如图,直线是一次函数的图象,若点在直线上,则的值是(? ? ? ? )
A. B. C. D.
4. 如图,在平面直角坐标系中, ,,点是轴上任意一点,当有最小值时,点的坐标为(? ? ? ? )
A. B. C. D.
5. 若关于的方程的解为,则直线一定经过点(? ? ? ? ? )
A. B. C. D.
6. 已知与成正比例,当=时,=.则当=时,的值是(? ? ? ? )
A. B. C. D.
7. 若三点,,在同一条直线上,则a的值为(? ? ? ? ?)
A. B. C. D.
8. 若直线与直线的交点在轴上,则的值为(? ? ? ? )
A. B. C. D.
9. 如果直线与两坐标轴围成的三角形的面积是,那么m的值是? ? ? ?
A. B. C. D.
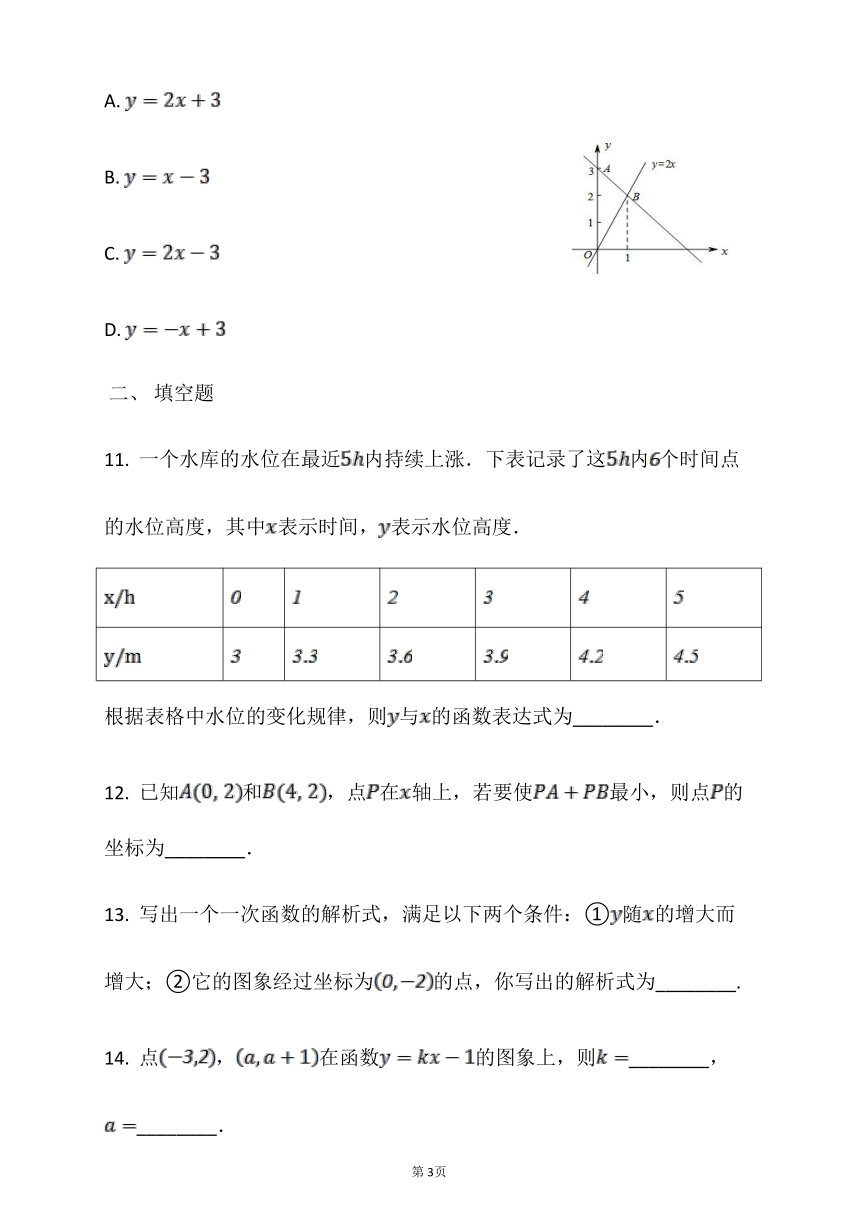
10. 如图,过点的一次函数的图象与正比例函数的图象相交于点,则这个一次函数的解析式是? ? ? ?
A.
B.
C.
D.
二、 填空题?
11. 一个水库的水位在最近内持续上涨.下表记录了这内个时间点的水位高度,其中表示时间,表示水位高度.
根据表格中水位的变化规律,则与的函数表达式为________.
12. 已知和,点在轴上,若要使最小,则点的坐标为________.
13. 写出一个一次函数的解析式,满足以下两个条件:①随的增大而增大;②它的图象经过坐标为的点,你写出的解析式为________.
14. 点,在函数的图象上,则________,________.
15. 一次函数的图象经过点,并平行于直线=,那么此一次函数解析式为________.
三、 解答题
16. 已知一次函数的图象过,两点.
求这个一次函数的表达式;
试判断点是否在这个一次函数的图象上.
?
17. 已知直线平行于直线,且经过点.
求直线的解析式;
试说明点是否在直线上.
?
18. 某商店购进一批成本为每件元的商品,商店按单价不低于成本价,且不高于元销售.经调查发现,该商品每天的销售量(件)与销售单价(元)之间满足一次函数关系,其图象如图所示.
求该商品每天的销售量(件)与销售单价(元)之间的函数关系式;
销售单价定为多少元时,才能使销售该商品每天获得的利润(元)最大?最大利润是多少?
参考答案与试题解析
19.2.2 《一次函数》-用待定系数法求一次函数解析式 同步习题(1)
一、 选择题
1.【答案】C
2.【答案】A
3.【答案】C
4.【答案】D
5.【答案】A
6.【答案】D
7.【答案】C
8.【答案】C
9.【答案】D
10.【答案】D
二、 填空题
11.【答案】
12.【答案】
13.【答案】
(只要满足题意即可)
14.【答案】;
15.【答案】=
三、 解答题
16.【答案】
解:设一次函数表达式为?,将,代入,
得
?解得
故一次函数表达式为.
把代入,解得,
故点?不在一次函数图象上.
17.【答案】
解:依题意可设直线?的解析式为?,
将点代入可得?,
解得?,
∴ 直线的解析式为?.
∵ ?时,
,
∴ 点不在直线上.
18.【答案】
解:设与销售单价之间的函数关系式为:,
将点,代入一次函数表达式得:
解得:
故函数的表达式为:.
由题意得:
,
∵ ,故当时,随的增大而增大,而,
∴ 当时,有最大值,此时,,
故销售单价定为元时,该超市每天的利润最大,最大利润元.
试卷第2 22页,总8 88页
第1 11页
一、 选择题
1. 一次函数的图象经过点,每当x增加个单位时,增加个单位,则此函数表达式是(? ? ? ? )
A. B. C. D.
2. 若一次函数的图象经过,两点,则的值为(????????)
A. B. C. D.
3. 如图,直线是一次函数的图象,若点在直线上,则的值是(? ? ? ? )
A. B. C. D.
4. 如图,在平面直角坐标系中, ,,点是轴上任意一点,当有最小值时,点的坐标为(? ? ? ? )
A. B. C. D.
5. 若关于的方程的解为,则直线一定经过点(? ? ? ? ? )
A. B. C. D.
6. 已知与成正比例,当=时,=.则当=时,的值是(? ? ? ? )
A. B. C. D.
7. 若三点,,在同一条直线上,则a的值为(? ? ? ? ?)
A. B. C. D.
8. 若直线与直线的交点在轴上,则的值为(? ? ? ? )
A. B. C. D.
9. 如果直线与两坐标轴围成的三角形的面积是,那么m的值是? ? ? ?
A. B. C. D.
10. 如图,过点的一次函数的图象与正比例函数的图象相交于点,则这个一次函数的解析式是? ? ? ?
A.
B.
C.
D.
二、 填空题?
11. 一个水库的水位在最近内持续上涨.下表记录了这内个时间点的水位高度,其中表示时间,表示水位高度.
根据表格中水位的变化规律,则与的函数表达式为________.
12. 已知和,点在轴上,若要使最小,则点的坐标为________.
13. 写出一个一次函数的解析式,满足以下两个条件:①随的增大而增大;②它的图象经过坐标为的点,你写出的解析式为________.
14. 点,在函数的图象上,则________,________.
15. 一次函数的图象经过点,并平行于直线=,那么此一次函数解析式为________.
三、 解答题
16. 已知一次函数的图象过,两点.
求这个一次函数的表达式;
试判断点是否在这个一次函数的图象上.
?
17. 已知直线平行于直线,且经过点.
求直线的解析式;
试说明点是否在直线上.
?
18. 某商店购进一批成本为每件元的商品,商店按单价不低于成本价,且不高于元销售.经调查发现,该商品每天的销售量(件)与销售单价(元)之间满足一次函数关系,其图象如图所示.
求该商品每天的销售量(件)与销售单价(元)之间的函数关系式;
销售单价定为多少元时,才能使销售该商品每天获得的利润(元)最大?最大利润是多少?
参考答案与试题解析
19.2.2 《一次函数》-用待定系数法求一次函数解析式 同步习题(1)
一、 选择题
1.【答案】C
2.【答案】A
3.【答案】C
4.【答案】D
5.【答案】A
6.【答案】D
7.【答案】C
8.【答案】C
9.【答案】D
10.【答案】D
二、 填空题
11.【答案】
12.【答案】
13.【答案】
(只要满足题意即可)
14.【答案】;
15.【答案】=
三、 解答题
16.【答案】
解:设一次函数表达式为?,将,代入,
得
?解得
故一次函数表达式为.
把代入,解得,
故点?不在一次函数图象上.
17.【答案】
解:依题意可设直线?的解析式为?,
将点代入可得?,
解得?,
∴ 直线的解析式为?.
∵ ?时,
,
∴ 点不在直线上.
18.【答案】
解:设与销售单价之间的函数关系式为:,
将点,代入一次函数表达式得:
解得:
故函数的表达式为:.
由题意得:
,
∵ ,故当时,随的增大而增大,而,
∴ 当时,有最大值,此时,,
故销售单价定为元时,该超市每天的利润最大,最大利润元.
试卷第2 22页,总8 88页
第1 11页
