7.2.1用坐标表示地理位置 课件(共21张PPT)
文档属性
| 名称 | 7.2.1用坐标表示地理位置 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-08 00:00:00 | ||
图片预览







文档简介
7.2.1用坐标表示地理位置
2021年春人教版七年级数学下册
第七章 平面直角坐标系
1、根据实际情况,建立合适的平面直角坐标系。
2、用坐标表示地理位置。
3、用平面角和距离表示两个物体的相对位置。
在平面直角坐标系中用坐标表示地理位置。(重点)
用平面角和距离表示两个物体的相对位置。( 难点)
学习目标
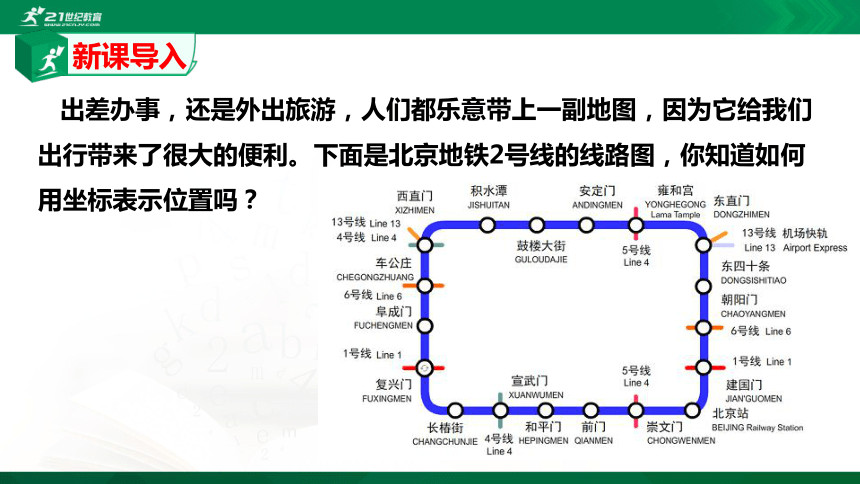
出差办事,还是外出旅游,人们都乐意带上一副地图,因为它给我们出行带来了很大的便利。下面是北京地铁2号线的线路图,你知道如何用坐标表示位置吗?
新课导入
探究: 根据以下条件画一幅示意图,标出学校和小刚家、小强家、小敏家的位置。
小刚家:出校门向东走1 500 m,再向北走2 000 m.
小强家:出校门向西走2 000 m,再向北走3 500 m,最后向东走500 m。
小敏家:出校门向南走1 000 m,再向东走3 000 m,最后向南走750 m。
思考:
你能利用平面直角坐标系描述几位同学家的位置吗?
你打算怎样建立平面直角坐标系?
你能在所作的平面直角坐标系中确定各位置的坐标吗?
探究新知
x/m
y/m
小刚家
(1500,2000)
学校
小强家
(-1500,3500)
小敏家
(3000,-1750)
1000
1000
-1000
-1000
-2000
2000
O
小刚家:出校门向东走1 500 m,再向北走2 000 m.
小强家:出校门向西走2 000 m,再向北走3 500 m,最后向东走500 m.
小敏家:出校门向南走1 000 m,再向东走3 000 m,最后向南走750 m.
(0,0)
3000
2000
3000
-2000
3、在坐标平面内画出这些点,写出各点的______和各个地点的名称。
归纳
1、建立坐标系,选择一个适当的参照点为____,确定X轴、Y轴的______。
2、根据具体问题确定适当的_______,在坐标轴上标出__________。
一般步骤是什么吗?
原点
正方向
比例尺
单位长度
坐标
思考:在解决问题的过程中你是怎么做的?你能归纳步骤吗?
思考归纳
·
猴山
(2,1)
·
狮虎山
(8,2)
已知猴山的坐标为(2,1),狮虎山的坐标为(8,2),而熊猫馆的坐标为(6,6)。你能在图中标出熊猫馆的位置吗?(向上、向右为正)
1
2
0
8
4
5
6
7
3
x
y
1
2
6
3
4
5
7
8
熊猫馆
(6,6)
·
提示:由猴山和狮虎山的坐标确定原点位置和单位长度
例题讲解
思考: 我们知道,通过建立平面直角坐标系,可以用坐标表示平面内点的位置。
还有其他方法吗?
用方位角和距离表示具体位置
探索与思考
北
5nmile
60°
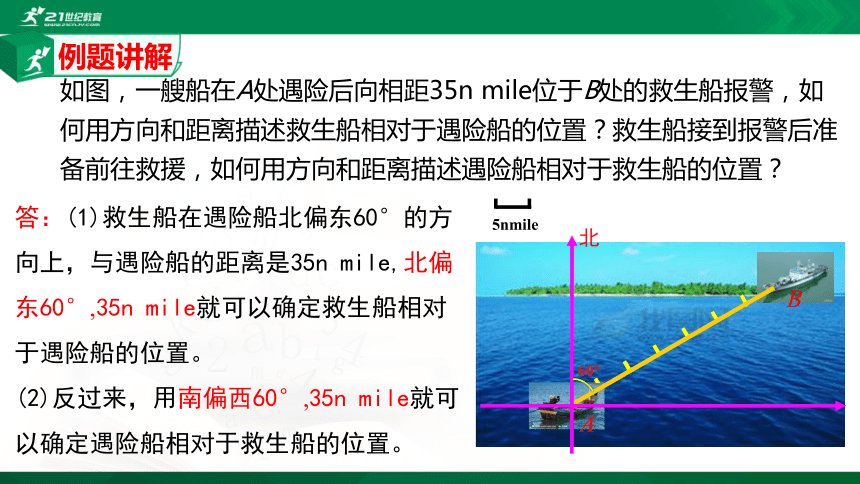
如图,一艘船在A处遇险后向相距35n mile位于B处的救生船报警,如何用方向和距离描述救生船相对于遇险船的位置?救生船接到报警后准备前往救援,如何用方向和距离描述遇险船相对于救生船的位置?
A
B
答:(1)救生船在遇险船北偏东60°的方向上,与遇险船的距离是35n mile,北偏东60°,35n mile就可以确定救生船相对于遇险船的位置。
(2)反过来,用南偏西60°,35n mile就可以确定遇险船相对于救生船的位置。
例题讲解
-3 -2 -1 1 2 3 4 5 x
y
0
1
-1
-2
-3
-4
A(-3,-2)
A(-3,-2)
向右平移5个单位
B
B
C
A(-3,-2)
向右平移7个单位
C
横坐标、纵坐标分别发生了什么变化
●
●
●
点在平面直角坐标系中的平移
(2,-2)
(4,-2)
(-3+a,-2)
A(-3,-2)
向右平移a个单位
a >0
-4- 3 -2 -1 1 2 3 4 5 x
y
0
1
-1
-2
-3
-4
A(3,-2)
向左平移5个单位
B
A(3,-2)
向左平移7个单位
C
A(3,-2)
●
●
●
B
C
A(3,-2)
向左平移a个单位
a >0
(-2,-2)
(-4,-2)
(3-a,-2)
(1)左、右平移:
向右平移a个单位( )
原图形上的点(x,y) ,
向左平移a个单位( )
原图形上的点(x,y) ,
x+a,y
x-a,y
总结规律:图形平移与点的坐标变化间的关系
左右平移,纵坐标不变,横坐标变化(左减右加)
归纳小结
1.将点A(1,2)向右平移2个单位长度,得到A' , 则A'的坐标为______。
2.将点A(3,1)向右平移3个单位长度,得到A’ ,则A’的坐标为______。
3.将点A(3,-2)向左平移4个单位长度,得到A’,则A’的坐标为______。
4.将点A(0,-2)向左平移2个单位长度,得到A’,则A’的坐标为______。
(3,2)
(6,1)
(-1,-2)
(-2,-2)
针对练习
-4- 3 -2 -1 1 2 3 4 5 x
y
0
4
2
1
3
-1
A(3,-1)
A(3,-1)
向上平移3个单位
B
(3,2)
B
C
A(3,-1)
向上平移5个单位
C
(3,4)
(3,-1+b)
A(3,-1)
向上平移b个单位
b >0
●
●
●
观察发现
-4- 3 -2 -1 1 2 3 4 5 x
y
0
4
2
1
3
-1
A(3,4)
A(3,4)
向下平移3个单位
B
(3,1)
B
C
A(3,4)
向下平移5个单位
C
(3,-1)
(3,4-b)
A(3,4)
向下平移b个单位
b >0
●
●
●
(2)上、下平移:
向上平移b个单位( )
原图形上的点(x,y) ,
向下平移b个单位( )
原图形上的点(x,y) ,
x,y+b
x,y-b
总结规律:图形平移与点的坐标变化间的关系
上下平移,横坐标不变,纵坐标变化(下减上加)
归纳小结
1.将点A(3,2) 向上平移2个单位长度,得到A' ,则A'的坐标为______。
2.将点A(3,-2)向下平移3个单位长度,得到A’,则A’的坐标为______。
3.将点A(0,2) 向上平移4个单位长度,得到A’,则
A’的坐标为______。
4.将点A(-3,-2)向上平移2个单位长度,得到A’,则A’的坐标为______。
(3,4)
(3,-5)
(0,6)
(-3,0)
针对练习
已知点A(3,2),将点A先向右平移2个单位长度,再向上平移5个单位长度,得到A′,则A′的坐标为________。
(5,7)
已知点A(-3,2),将点A先向左平移2个单位长度,再向下平移5个单位长度,得到A′,则A′的坐标为________。
(-5,-3)
课堂练习
用坐标表示地理位置:
1、建立坐标系,选择一个适当的参照点为原点,确定X轴、Y轴的正方向。
2、根据具体问题确定适当的比例尺,在坐标轴上标出单位长度。
3、在坐标平面内画出这些点,写出各点的坐标和各个地点的名称。
用坐标表示平移:
左右平移,纵坐标不变,横坐标变化(左减右加)
上下平移,横坐标不变,纵坐标变化(下减上加)
课堂小结
谢谢聆听
2021年春人教版七年级数学下册
第七章 平面直角坐标系
1、根据实际情况,建立合适的平面直角坐标系。
2、用坐标表示地理位置。
3、用平面角和距离表示两个物体的相对位置。
在平面直角坐标系中用坐标表示地理位置。(重点)
用平面角和距离表示两个物体的相对位置。( 难点)
学习目标
出差办事,还是外出旅游,人们都乐意带上一副地图,因为它给我们出行带来了很大的便利。下面是北京地铁2号线的线路图,你知道如何用坐标表示位置吗?
新课导入
探究: 根据以下条件画一幅示意图,标出学校和小刚家、小强家、小敏家的位置。
小刚家:出校门向东走1 500 m,再向北走2 000 m.
小强家:出校门向西走2 000 m,再向北走3 500 m,最后向东走500 m。
小敏家:出校门向南走1 000 m,再向东走3 000 m,最后向南走750 m。
思考:
你能利用平面直角坐标系描述几位同学家的位置吗?
你打算怎样建立平面直角坐标系?
你能在所作的平面直角坐标系中确定各位置的坐标吗?
探究新知
x/m
y/m
小刚家
(1500,2000)
学校
小强家
(-1500,3500)
小敏家
(3000,-1750)
1000
1000
-1000
-1000
-2000
2000
O
小刚家:出校门向东走1 500 m,再向北走2 000 m.
小强家:出校门向西走2 000 m,再向北走3 500 m,最后向东走500 m.
小敏家:出校门向南走1 000 m,再向东走3 000 m,最后向南走750 m.
(0,0)
3000
2000
3000
-2000
3、在坐标平面内画出这些点,写出各点的______和各个地点的名称。
归纳
1、建立坐标系,选择一个适当的参照点为____,确定X轴、Y轴的______。
2、根据具体问题确定适当的_______,在坐标轴上标出__________。
一般步骤是什么吗?
原点
正方向
比例尺
单位长度
坐标
思考:在解决问题的过程中你是怎么做的?你能归纳步骤吗?
思考归纳
·
猴山
(2,1)
·
狮虎山
(8,2)
已知猴山的坐标为(2,1),狮虎山的坐标为(8,2),而熊猫馆的坐标为(6,6)。你能在图中标出熊猫馆的位置吗?(向上、向右为正)
1
2
0
8
4
5
6
7
3
x
y
1
2
6
3
4
5
7
8
熊猫馆
(6,6)
·
提示:由猴山和狮虎山的坐标确定原点位置和单位长度
例题讲解
思考: 我们知道,通过建立平面直角坐标系,可以用坐标表示平面内点的位置。
还有其他方法吗?
用方位角和距离表示具体位置
探索与思考
北
5nmile
60°
如图,一艘船在A处遇险后向相距35n mile位于B处的救生船报警,如何用方向和距离描述救生船相对于遇险船的位置?救生船接到报警后准备前往救援,如何用方向和距离描述遇险船相对于救生船的位置?
A
B
答:(1)救生船在遇险船北偏东60°的方向上,与遇险船的距离是35n mile,北偏东60°,35n mile就可以确定救生船相对于遇险船的位置。
(2)反过来,用南偏西60°,35n mile就可以确定遇险船相对于救生船的位置。
例题讲解
-3 -2 -1 1 2 3 4 5 x
y
0
1
-1
-2
-3
-4
A(-3,-2)
A(-3,-2)
向右平移5个单位
B
B
C
A(-3,-2)
向右平移7个单位
C
横坐标、纵坐标分别发生了什么变化
●
●
●
点在平面直角坐标系中的平移
(2,-2)
(4,-2)
(-3+a,-2)
A(-3,-2)
向右平移a个单位
a >0
-4- 3 -2 -1 1 2 3 4 5 x
y
0
1
-1
-2
-3
-4
A(3,-2)
向左平移5个单位
B
A(3,-2)
向左平移7个单位
C
A(3,-2)
●
●
●
B
C
A(3,-2)
向左平移a个单位
a >0
(-2,-2)
(-4,-2)
(3-a,-2)
(1)左、右平移:
向右平移a个单位( )
原图形上的点(x,y) ,
向左平移a个单位( )
原图形上的点(x,y) ,
x+a,y
x-a,y
总结规律:图形平移与点的坐标变化间的关系
左右平移,纵坐标不变,横坐标变化(左减右加)
归纳小结
1.将点A(1,2)向右平移2个单位长度,得到A' , 则A'的坐标为______。
2.将点A(3,1)向右平移3个单位长度,得到A’ ,则A’的坐标为______。
3.将点A(3,-2)向左平移4个单位长度,得到A’,则A’的坐标为______。
4.将点A(0,-2)向左平移2个单位长度,得到A’,则A’的坐标为______。
(3,2)
(6,1)
(-1,-2)
(-2,-2)
针对练习
-4- 3 -2 -1 1 2 3 4 5 x
y
0
4
2
1
3
-1
A(3,-1)
A(3,-1)
向上平移3个单位
B
(3,2)
B
C
A(3,-1)
向上平移5个单位
C
(3,4)
(3,-1+b)
A(3,-1)
向上平移b个单位
b >0
●
●
●
观察发现
-4- 3 -2 -1 1 2 3 4 5 x
y
0
4
2
1
3
-1
A(3,4)
A(3,4)
向下平移3个单位
B
(3,1)
B
C
A(3,4)
向下平移5个单位
C
(3,-1)
(3,4-b)
A(3,4)
向下平移b个单位
b >0
●
●
●
(2)上、下平移:
向上平移b个单位( )
原图形上的点(x,y) ,
向下平移b个单位( )
原图形上的点(x,y) ,
x,y+b
x,y-b
总结规律:图形平移与点的坐标变化间的关系
上下平移,横坐标不变,纵坐标变化(下减上加)
归纳小结
1.将点A(3,2) 向上平移2个单位长度,得到A' ,则A'的坐标为______。
2.将点A(3,-2)向下平移3个单位长度,得到A’,则A’的坐标为______。
3.将点A(0,2) 向上平移4个单位长度,得到A’,则
A’的坐标为______。
4.将点A(-3,-2)向上平移2个单位长度,得到A’,则A’的坐标为______。
(3,4)
(3,-5)
(0,6)
(-3,0)
针对练习
已知点A(3,2),将点A先向右平移2个单位长度,再向上平移5个单位长度,得到A′,则A′的坐标为________。
(5,7)
已知点A(-3,2),将点A先向左平移2个单位长度,再向下平移5个单位长度,得到A′,则A′的坐标为________。
(-5,-3)
课堂练习
用坐标表示地理位置:
1、建立坐标系,选择一个适当的参照点为原点,确定X轴、Y轴的正方向。
2、根据具体问题确定适当的比例尺,在坐标轴上标出单位长度。
3、在坐标平面内画出这些点,写出各点的坐标和各个地点的名称。
用坐标表示平移:
左右平移,纵坐标不变,横坐标变化(左减右加)
上下平移,横坐标不变,纵坐标变化(下减上加)
课堂小结
谢谢聆听
